جواب تمرین صفحه 123 درس 9 ریاضی هفتم (آمار و احتمال)
تعداد بازدید : 86.39Mپاسخ تمرین صفحه 123 ریاضی هفتم
-گام به گام تمرین صفحه 123 درس آمار و احتمال
-تمرین صفحه 123 درس 9
-شما در حال مشاهده جواب تمرین صفحه 123 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
١ عقربهٔ چرخندهٔ روبه رو را می چرخانیم؛ احتمال ایستادن عقربه روی کدام رنگ بیشتر است؟ چرا؟
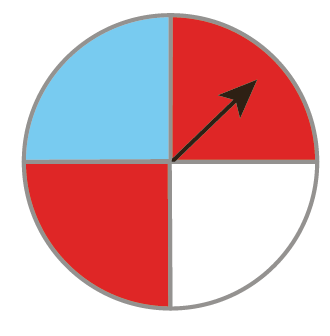
رنگ قرمز؛ زیرا ۲ قسمت از ۴ قسمت را به خود اختصاص داده و باقی رنگها ۱ قسمت از ۴ قسمت را.
٢ در یک کیسه ٤ مهرهٔ آبی و ١ مهرهٔ قرمز قرار داده ایم.
یک مهره را به طور تصادفی بیرون می آوریم، رنگ آن را یادداشت می کنیم و به کیسه برمی گردانیم.
می خواهیم این آزمایش را ٢٠ بار انجام دهیم.
آیا می توانیم پیش از انجام کار، مشخص کنیم که در چه کسری از آزمایش ها مهرهٔ آبی بیرون می آید؟ چرا؟
به صورت دقیق نمی توان مشخص کرد؛ زیرا که همیشه امکان دارد که با چند تا عدد جابجا شود. ولی به صورت تقریبی انتظار داریم که ۱۶ بار مهره آبی ظاهر شود؛ زیرا ۴ مهره از ۵ مهره آبی است و:
\(\frac{4}{5} \times 20 = 16\)
٣ یک تاس را 20 بار، پرتاب و نتیجهٔ آزمایش ها را در جدول یادداشت کرده ایم:

الف هر یک از عددهای روی تاس، در چه کسری از آزمایش ها آمده است؟
ب آیا می توانید بدون محاسبه، حاصل جمع این کسرها را به دست آورید؟ چگونه؟
الف
\( = \frac{2}{{20}}\) کسر عدد 1
\( = \frac{4}{{20}}\) کسر عدد 2
\( = \frac{4}{{20}}\) کسر عدد 3
\( = \frac{4}{{20}}\) کسر عدد 4
\( = \frac{5}{{20}}\) کسر عدد 5
\( = \frac{1}{{20}}\) کسر عدد 6
ب
بله؛ چون هر آزمایش \(\frac{1}{{20}}\) کل آزمایش را تشکیل می دهد، بنابراین برای کل آزمایش ها داریم:
\(\frac{1}{{20}} \times 20 = 1\)
٤ الف انتظار دارید در ١٠٠٠ بار پرتاب تاس، تقریباً چند بار 0 بیاید؟
ب انتظار دارید در ١٠٠٠ بار پرتاب تاس، تقریباً چند بار عددی زوج بیاید؟
الف
تقریبا 167 بار؛ زیرا:
\(\frac{1}{6} \times 1000 \simeq 167\)
ب
تقریبا 500 بار؛ زیرا 3 عدد زوج بر روی تاس وجود دارد، پس:
\(\frac{3}{6} \times 1000 = 500\)
5 چرخندهٔ مقابل را طوری رنگ کنید که احتمال ایستادن عقربه روی رنگ سفید، برابر صفر باشد؛ یعنی ایستادن عقربه روی رنگ سفید، غیرممکن شود.
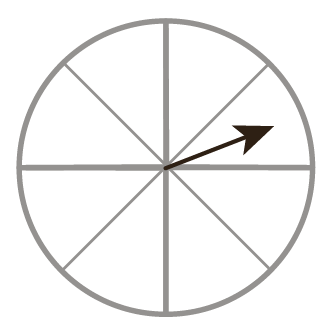
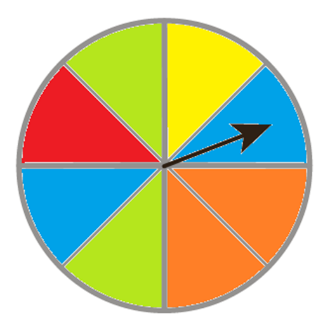
6 عقربهٔ چرخندهٔ مقابل را می چرخانیم.
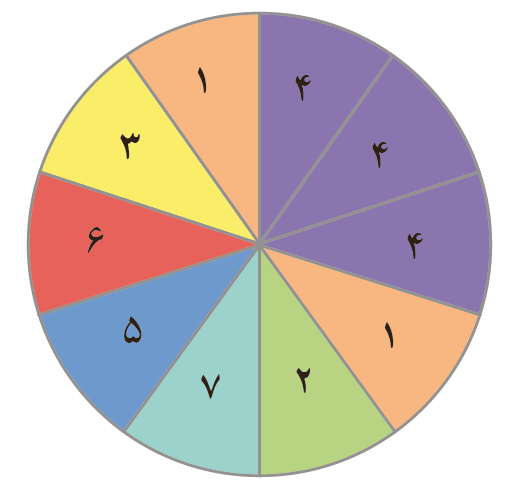
الف احتمال ایستادن عقربه روی هر یک از عددها را محاسبه کنید.
= احتمال ٣ = احتمال ٢ = احتمال ١
= احتمال 6 = احتمال 5 = احتمال 4
ب اگر ١٠٠٠ بار عقربه را بچرخانیم، انتظار داریم عقربه تقریباً چند بار روی عدد ٣ قرار بگیرد؟
ج اگر ١٠٠٠ بار عقربه را بچرخانیم، انتظار داریم عقربه تقریباً چند بار روی عدد ٤ قرار بگیرد؟
الف
\( = \frac{1}{{10}}\) احتمال ٣ \( = \frac{1}{{10}}\) احتمال ٢ \( = \frac{2}{{10}}\) احتمال ١
\( = \frac{1}{{10}}\) احتمال 6 \( = \frac{1}{{10}}\) احتمال 5 \( = \frac{1}{{10}}\) احتمال 4
ب
100 دفعه قرار می گیرد روی عدد 3.
\(\frac{1}{{10}} \times 1000 = 100\)
ج
300 دفعه قرار می گیرد روی عدد 4.
\( = \frac{3}{{10}}\) احتمال آمدن عدد 4
\(\frac{3}{{10}} \times 1000 = 300\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















