جواب تمرین صفحه 21 درس 1 حسابان دوازدهم (تابع)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 21 حسابان دوازدهم
-گام به گام تمرین صفحه 21 درس تابع
-تمرین صفحه 21 درس 1
-شما در حال مشاهده جواب تمرین صفحه 21 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 تابع \(f\left( x \right) = {\left( {x - 2} \right)^3} + 1\) را درنظر بگیرید.
الف نمودار تابع f را به کمک نمودار تابع \(y = {x^3}\) رسم کنید.
ب نشان دهید که f وارون پذیر است و نمودار f-1 را رسم کنید.
پ ضابطه f-1 را به دست آورید.
الف
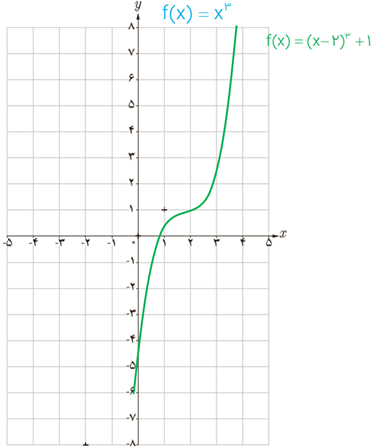
ب
تابع f یک تابع یک به یک است؛ در نتیجه :
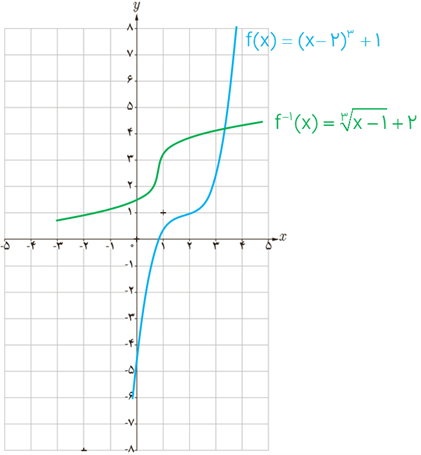
پ
\(\begin{array}{l}f(x) = y = {(x - 2)^3} + 1 \Rightarrow y - 1 = {(x - 2)^3} \Rightarrow x - 2 = \sqrt[3]{{y - 1}} \Rightarrow x = \sqrt[3]{{y - 1}} + 2\\ \Rightarrow y = \sqrt[3]{{x - 1}} + 2\\ \Rightarrow {f^{ - 1}}(x) = \sqrt[3]{{x - 1}} + 2\end{array}\)
2 نمودار توابع f، g و h در زیر رسم شده اند.
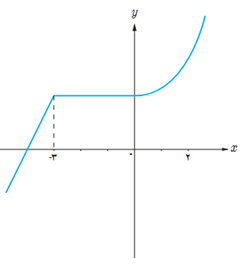
\(y = f(x)\)
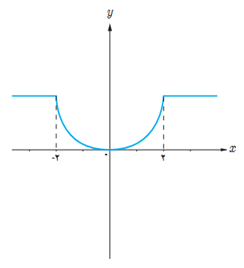
\(y = g(x)\)
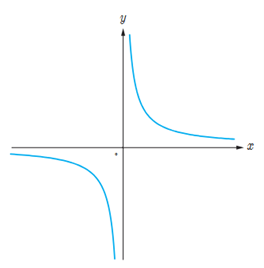
\(y = h(x)\)
الف تابع f در چه فاصله هایی اکیداً صعودی و در چه فاصله هایی صعودی است؟
ب تابع g در چه فاصله هایی اکیداً نزولی و در چه فاصله هایی نزولی است؟
پ تابع h در چه فاصله هایی اکیداً نزولی است؟
الف
تابع f در بازه های \(\left( { - \infty \;,\;3} \right]\) و\(\left[ {0,\;\infty } \right)\) اکیداً صعودی و در تمام نقاط صعودی است.
ب
تابع g در بازه های [-2,0] اکیداً نزولی و در بازه های \(\left( { - \infty \;,\; - 2} \right]\) و \(\left[ {2,\;\infty } \right)\) نزولی است.
پ
تابع g در بازه های [-2,0] اکیداً نزولی و در بازه های \(\left( { - \infty \;,\; - 2} \right]\) و \(\left[ {2,\;\infty } \right)\) نزولی است.
3 نمودار هر یک از توابع زیر را رسم کنید. کدام یک از آنها در تمام دامنه خود، اکیداً یکنواست؟
الف \(f\left( x \right) = \sqrt {2 - x} \)
ب \(g\left( x \right) = {2^{ - x}}\)
پ \(h\left( x \right) = {\log _2}x\)
الف
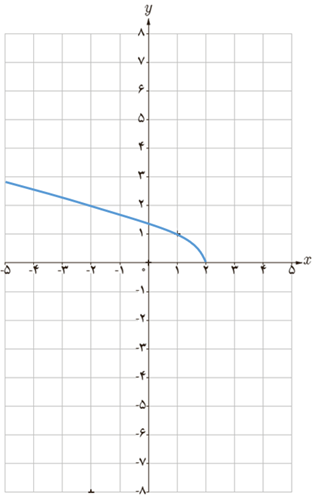
ب
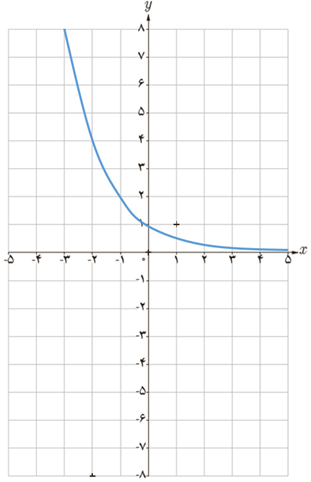
پ
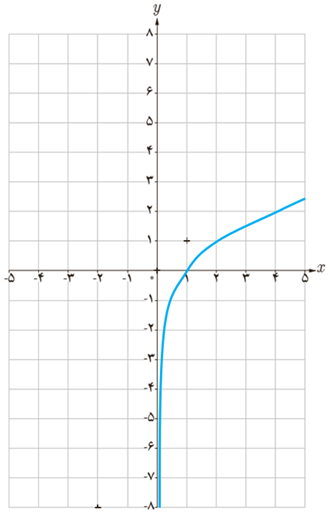
همه اکیداً یکنوا هستند.
4
الف آیا تابعی وجود دارد که در یک فاصله، هم صعودی و هم نزولی باشد؟
ب نمودار تابعی را رسم کنید که در هریک از بازه های \(\left( { - \infty \;,\;0} \right)\) و \(\left[ {0\;,\; + \infty } \right)\) اکیداً صعودی باشد ولی در R اکیداً صعودی نباشد.
الف
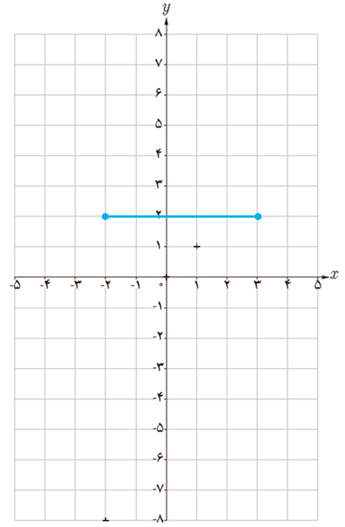
بله؛ مثال :
تابع ثابت f(x)=2 در فاصله [-2,3] هم صعودی است و هم نزولی.
ب
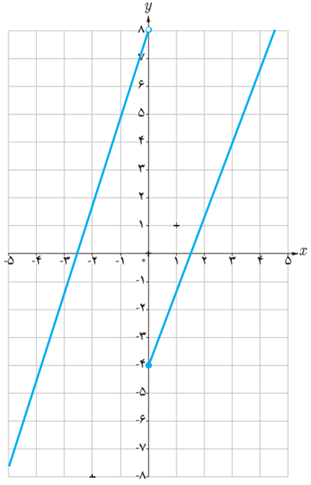
5 اگر توابع f و g در یک فاصله اکیداً صعودی باشند، نشان دهید که تابع f+g نیز در این فاصله اکیداً صعودی است. برای تابع f-g چه می توان گفت؟
تابع f روی فاصله I اکیدا صعودی است؛ بنابراین :
\(\forall \;a\;,\;b \in I\quad ,\quad a < b\quad \Rightarrow f(a) < f(b)\)
تابع g روی فاصله I اکیدا صعودی است؛ بنابراین :
\(\forall \;a\;,\;b \in I\quad ,\quad a < b\quad \Rightarrow g(a) < g(b)\)
داریم:
\( \Rightarrow f(a) + g(a) < f(b) + g(b) \Rightarrow \forall \;a\;,\;b \in I\quad ,\quad a < b\quad :\quad (f + g)(a) < (f + g)(b)\)
در نتیجه تابع f + g روی فاصله I اکیدا صعودی است.
برای تابع f - g داریم :
نمی توان گفت همواره تابع f - g نیز اکیداً صعودی است. مثال نقض :
توابع \(f(x) = 2x + 4\) و \(g(x) = 5x + 4\) روی دامنه خود اکیداً صعودی هستند ولی :
\((f - g)(x) = (2x + 4) - (5x + 4) = - 3x\)
که یک تابع اکیداً نزولی می باشد.
6 اگر باقی مانده تقسیم چند جمله ای \({x^3} + k{x^2} + 2\) بر x-2 برابر با 6 باشد، k را تعیین کنید.
\(\left. \begin{array}{l}f(x) = {x^3} + k{x^2} + 2\\p(x) = x - 2\\r(x) = 6\end{array} \right\} \Rightarrow p(x) = 0 \Rightarrow x - 2 = 0 \Rightarrow x = 2 \Rightarrow r(x) = f(2) \Rightarrow 6 = 4k + 10 \Rightarrow k = - 1\)
7 مقادیر a و b را طوری تعیین کنید که چند جمله ای \(x3 + a{x^2} + bx + 1\) بر x-2 و x+1 بخش پذیر باشد.
\(\left. \begin{array}{l}f(x) = {x^3} + a{x^2} + bx + 1\\x - 2 = 0 \Rightarrow x = 2 \Rightarrow f(2) = 0\\x + 1 = 0 \Rightarrow x = - 1 \Rightarrow f( - 1) = 0\end{array} \right\} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{4a + 2b = - 9}\\{a - b = 0\quad \;\;}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 1/5}\\{b = - 1/5}\end{array}} \right.\)
8 هر یک از چند جمله ای های زیر را بر حسب عامل های خواسته شده تجزیه کنید.
الف \({x^6} - 1\) با عامل x - 1
ب \({x^6} - 1\) با عامل x + 1
پ \({x^5} + 32\) با عامل x + 2
الف
\({x^6} - 1 = {x^6} - {1^6} = (x - 1)({x^5} + {x^4} + {x^3} + {x^2} + x + 1)\)
ب
\({x^6} - 1 = {x^6} - {1^6} = (x + 1)({x^5} - {x^4} + {x^3} - {x^2} + x - 1)\)
پ
\({x^5} + 32 = {x^5} + {2^5} = (x + 2)({x^4} - 2{x^3} + 4{x^2} - 8x + 16)\)
9
الف فرض کنید تابع f در یک بازه اکیداً نزولی باشد و a و b متعلق به این بازه باشند. اگر f(a)≤f(b) نشان دهید که a≥b.
ب اگر\({(\frac{1}{2})^{3x - 2}}\; \le \;\frac{1}{{64}}\) ، حدود x را به دست آورید.
الف
اثبات (برهان خلف):
فرض کنید a بزرگتر مساوی b نیست؛ بنابراین a<b می باشد؛ از طرفی چون f روی فاصله مذکور اکیداً نزولی است، بنابراین برای هر a و b عضو این فاصله a<b نتیجه می شود \(f(a) > f(b)\) و این خلاف فرض \(f(a) \le f(b)\) موجود در صورت سوال می باشد. از این تناقض نتیجه می شود فرض برهان خلف باطل است و \(a \ge b\) می باشد.
ب
\(\begin{array}{l}{(\frac{1}{2})^{3x - 2}} \le \frac{1}{{64}} \Rightarrow {(\frac{1}{2})^{3x - 2}} \le {(\frac{1}{2})^6} \Rightarrow {(2)^{ - (3x - 2)}} \le {(2)^{ - 6}} \Rightarrow - (3x - 2) \le - 6\\ \Rightarrow 3x - 2 \ge 6 \Rightarrow x \ge \frac{8}{3}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















