جواب تمرین صفحه 112 درس 5 ریاضی دوازدهم تجربی (کاربرد مشتق)
تعداد بازدید : 86.5Mپاسخ تمرین صفحه 112 ریاضی دوازدهم تجربی
-گام به گام تمرین صفحه 112 درس کاربرد مشتق
-تمرین صفحه 112 درس 5
-شما در حال مشاهده جواب تمرین صفحه 112 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 بزرگ ترین بازه از R که تابع \(f\left( x \right) = {x^2} - 12x + 4\) در آن نزولی اکید باشد، کدام است؟ چرا؟
\(\begin{array}{l}f'(x) = 3{x^2} - 12\;\;\mathop \Rightarrow \limits^{f'(x) = 0} \;\;3{x^2} - 12 = 0\\\\ \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2\end{array}\)
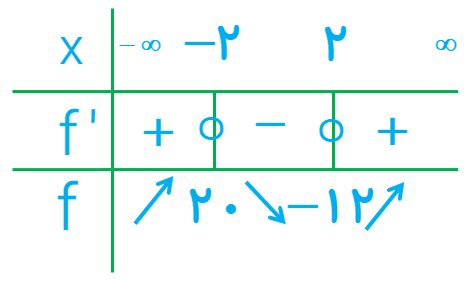
بزرگترین بازه که تابع در آن اکیداً نزولی است، بازه \(( - 2\;,\;2)\) است.
2 با تشکیل جدول تغییرات تابع \(g\left( x \right) = \frac{1}{{{x^2} + 1}}\) مشخص کنید تابع در چه بازه هایی صعودی اکید و در کدام بازه ها نزولی اکید است؟
\(\begin{array}{l}g'(x) = \frac{{ - 2x}}{{{{({x^2} + 1)}^2}}}\;\;\mathop \Rightarrow \limits^{g'(x) = 0} \;\;\frac{{ - 2x}}{{{{({x^2} + 1)}^2}}} = 0\\\\ \Rightarrow - 2x = 0 \Rightarrow x = 0\end{array}\)
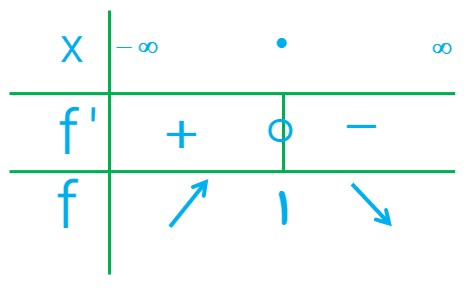
در بازه \(( - \,\infty \;,\;0)\) اکیداً صعودی و در بازه \((0\;,\;\infty )\) اکیداً نزولی است.
3 نقاط بحرانی توابع زیر را در صورت وجود به دست آورید.
الف \(f\left( x \right) = \sqrt {4 - {x^2}} \)
ب \(g\left( x \right) = {x^3} + 3{x^2} - 4\)
پ \(h\left( x \right) = \sqrt[3]{x}\)
الف \(f\left( x \right) = \sqrt {4 - {x^2}} \)
\(\begin{array}{l}f(x) = \sqrt {4 - {x^2}} \Rightarrow f'(x) = \frac{{ - 2x}}{{2\sqrt {4 - {x^2}} }} = \frac{{ - x}}{{\sqrt {4 - {x^2}} }}\\\\ \Rightarrow x = 0 \Rightarrow (0\;,\;2) \to \end{array}\)
نقطه بحرانی
ب \(g\left( x \right) = {x^3} + 3{x^2} - 4\)
\(\begin{array}{l}g(x) = {x^3} + 3{x^2} - 4 \Rightarrow g'(x) = 3{x^2} + 6x\\\\\mathop \Rightarrow \limits^{g'(x) = 0} \;\;3{x^2} + 6x = 0\\\\ \Rightarrow \left\{ \begin{array}{l}x = 0 \to (0\;,\; - 4)\\x = - 2 \to ( - 2\;,\;0)\end{array} \right. \to \end{array}\)
نقاط بحرانی
پ \(h\left( x \right) = \sqrt[3]{x}\)
\(h(x) = \sqrt[3]{x} \Rightarrow h'(x) = \frac{1}{{3\sqrt[3]{{{x^2}}}}} \to \)
در x=0 مشتق پذیر نیست و نقطه \((0\;,\;0)\) نقطه بحرانی است.
4 در هر یک از توابع زیر، ابتدا نقاط بحرانی تابع را به دست آورید و سپس با رسم جدول تغییرات تابع، نقاط ماکزیمم نسبی و مینیمم نسبی آن را در صورت وجود مشخص کنید.
الف \(f\left( x \right) = {x^3} + 3{x^2} - 9x - 10\)
ب \(g\left( x \right) = - 2{x^3} + 3{x^2} + 12x - 9\)
پ \(h\left( x \right) = - {x^3} - 3x + 2\)
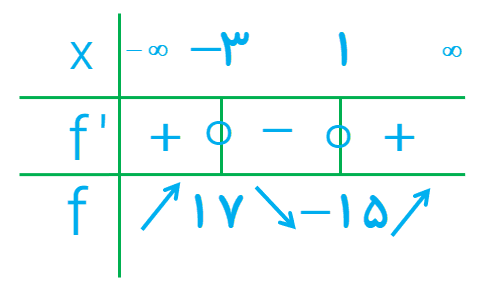
الف \(f\left( x \right) = {x^3} + 3{x^2} - 9x - 10\)
\(\begin{array}{l}f(x) = {x^3} + 3{x^2} - 9x - 10 \Rightarrow f'(x) = 3{x^2} + 6x - 9\\\\\mathop \Rightarrow \limits^{f'(x) = 0} \;3{x^2} + 6x - 9 = 0\\\\3(x - 1)(x + 3) = 0 \Rightarrow \left\{ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array}\)
نقاط بحرانی: \((1\;,\;15)\;,\;( - 3\;,\;17)\)
\(\max \;\left| \begin{array}{l} - 3\\17\end{array} \right.\quad ,\quad \min \;\left| \begin{array}{l}1\\ - 15\end{array} \right.\)
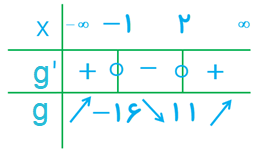
ب \(g\left( x \right) = - 2{x^3} + 3{x^2} + 12x - 9\)
\(\begin{array}{l}g(x) = - 2{x^3} + 3{x^2} + 12x - 9\\\\ \Rightarrow g'(x) = - 6{x^2} + 6x + 12\\\\\mathop \Rightarrow \limits^{g'(x) = 0} \;\; - 6{x^2} + 6x + 12 = 0\\\\ - 6(x - 2)(x + 1) = 0 \Rightarrow \left\{ \begin{array}{l}x = 2\\x = - 1\end{array} \right.\end{array}\)
نقاط بحرانی: \(( - 1\;,\; - 16)\;,\;(2\;,\;11)\)
\(\min \;\left| \begin{array}{l} - 1\\ - 16\end{array} \right.\quad ,\quad \max \;\left| \begin{array}{l}2\\11\end{array} \right.\)
پ \(h\left( x \right) = - {x^3} - 3x + 2\)
\(\begin{array}{l}h(x) = - {x^3} - 3x + 2 \Rightarrow g'(x) = - 3{x^2} - 3\\\\ \Rightarrow g'(x) \ne 0\end{array}\)
نقطه بحرانی ندارد
5 مقادیر ماکزیمم مطلق و مینیمم مطلق توابع زیر را در بازه های مشخص شده، در صورت وجود به دست آورید.
الف \(f\left( x \right) = - 2{x^3} + 9{x^2} - 13\;\;;\;\;x \in \left[ { - 1,2} \right]\)
ب \(g\left( x \right) = x3 + 2x - 5\;\;;\;\;x \in \left[ { - 2,1} \right]\)
الف \(f\left( x \right) = - 2{x^3} + 9{x^2} - 13\;\;;\;\;x \in \left[ { - 1,2} \right]\)
\(\begin{array}{l}f'(x) = - 6{x^2} + 18x = 0 \Rightarrow - 6x(x - 3) = 0\\\\ \to \left\{ \begin{array}{l}x = 0\\x = 3\quad \otimes \;:3 \notin \left[ { - 1\;,\;2} \right]\end{array} \right.\\\\x = - 1 \to y = - 2\\\\x = 0 \to y = - 13\\\\x = 2 \to y = 7\\\\\min \;\left| \begin{array}{l}0\\ - 13\end{array} \right.\quad ,\quad \max \;\left| \begin{array}{l}2\\7\end{array} \right.\end{array}\)
ب \(g\left( x \right) = x3 + 2x - 5\;\;;\;\;x \in \left[ { - 2,1} \right]\)
\(\begin{array}{l}g'(x) = 3{x^2} + 2 = 0 \Rightarrow {x^2} = - \frac{2}{3}\;\; \otimes \\\\x = - 2 \to y = - 17\\\\x = 1 \to y = - 2\\\\\min \;\left| \begin{array}{l} - 2\\ - 17\end{array} \right.\quad ,\quad \max \;\left| \begin{array}{l}1\\ - 2\end{array} \right.\end{array}\)
6 اگر نقطۀ (2,1)، نقطهٔ اکسترمم نسبی تابع \(f\left( x \right) = {x^3} + b{x^2} + d\) باشد، مقادیر b و d را به دست آورید.
\(\begin{array}{l}f(x) = {x^3} + b{x^2} + d\;\;\mathop \Rightarrow \limits^{(2\;,\;1)} \;\;1 = 8 + 4b + d \Rightarrow 4b + d = - 7\quad (1)\\\\f'(x) = 3{x^2} + 2bx\;\;\mathop \Rightarrow \limits^{f'(2) = 0} \;\;12 + 4b = 0 \Rightarrow b = - 3\\\\\mathop \Rightarrow \limits^{(1)} \;\;4( - 3) + d = - 7 \Rightarrow d = 5\end{array}\)
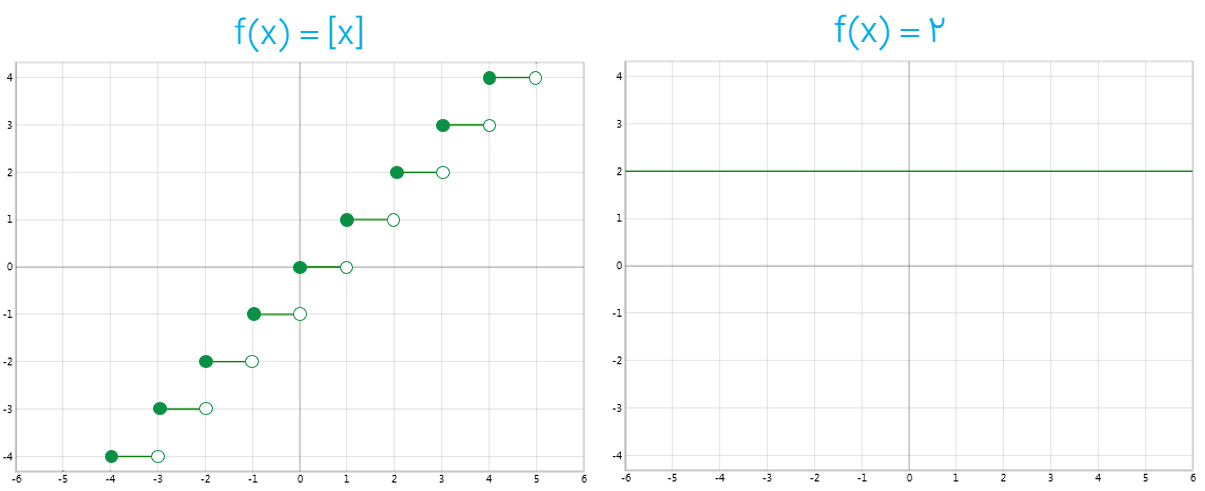
7 نمودار تابعی مانند f با دامنه R را رسم کنید به طوری که هر نقطهٔ دلخواه از Df یک نقطهٔ بحرانی f باشد. مسئله چند جواب دارد؟
تابع های جزء صحیح و تابع های ثابت:
\(\begin{array}{l}f(x) = \left[ x \right]\;\;\;\;\;x \in \mathbb{R}\\\\f(x) = k\;\;\;\;\;x \in \mathbb{R}\end{array}\)
مسئله بی شمار جواب دارد:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















