شاه کلید نکات
شاه کلید سوال
1 کشاورزی می خواهد دور یک مزرعه مستطیل شکل به مساحت ثابت 10000 متر مربع را دیوارکشی کند. هزینه هر متر دیوارهای شمالی و جنوبی 2 میلیون تومان و هزینه هر متر دیوارهای شرقی و غربی 8 میلیون تومان است.
الف هزینه مورد نیاز برای انجام این کار را به صورت یک تابع بنویسید.
ب ابعاد مزرعه چقدر باشد تا هزینه دیوارکشی به حداقل مقدار ممکن برسد؟
الف
\(\begin{array}{l}x\;y = 10,000 \Rightarrow y = \frac{{10,000}}{x}\\\\P(x) = 2(2,000,000x) + 2(8,000,000 \times \frac{{10,000}}{x})\\\\ = \frac{{4 \times {{10}^6}\;({x^2} + 40,000)}}{x}\end{array}\)
ب
\(\begin{array}{l}P'(x) = 4 \times {10^6}(\frac{{2{x^2} - {x^2} - 40,000}}{{{x^2}}}) = 4 \times {10^6}(\frac{{{x^2} - 40,000}}{{{x^2}}})\\\\\mathop \Rightarrow \limits^{P'(x) = 0} \;\;4 \times {10^6}(\frac{{{x^2} - 40,000}}{{{x^2}}}) = 0\\\\{x^2} = 40,000 \Rightarrow x = 200 \Rightarrow y = 50\end{array}\)
٢ الف می خواهیم کنار رودخانه یک محوطه به شکل مثلث متساوی الساقین را نرده کشی کنیم به طوری که قاعدهٔ مثلث منطبق بر رودخانه باشد. اگر تنها هزینه 100 متر نرده را در اختیار داشته باشیم، در این صورت بیشترین مساحت ممکن برای این مثلث چقدر خواهد بود؟
ب بدون استفاده از مشتق نیز، این مسئله را حل کنید.
الف
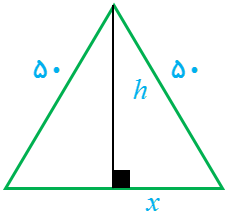
\(\begin{array}{l}{h^2} + {x^2} = {50^2} \Rightarrow h = \sqrt {2500 - {x^2}} \\\\S(x) = \frac{1}{2} \times 2x \times h = x\sqrt {2500 - {x^2}} \;\;\;D = \left[ {0\;,\;50} \right]\\\\S'(x) = \sqrt {2500 - {x^2}} + x \times \frac{{ - 2x}}{{2\sqrt {2500 - {x^2}} }}\\\\ = \frac{{2500 - {x^2} - {x^2}}}{{\sqrt {2500 - {x^2}} }} = \frac{{2500 - 2{x^2}}}{{\sqrt {2500 - {x^2}} }}\\\\\mathop \Rightarrow \limits^{S'(x) = 0} \;\;2500 - 2{x^2} = 0 \Rightarrow {x^2} = \frac{{2500}}{2} = 1250\\\\ \Rightarrow x = 25\sqrt 2 \\\\\mathop \Rightarrow \limits^{h = \sqrt {2500 - {x^2}} } \;\;h = \sqrt {2500 - 1250} = \sqrt {1250} \\\\ \Rightarrow h = 25\sqrt 2 \\\\S = x \times h = 25\sqrt 2 \times 25\sqrt 2 \Rightarrow S = 1250\end{array}\)
ب با توجه \(S = \frac{1}{2} \times 50 \times 50 \times \sin \theta \) بیشترین مساحت وقتی است که \(\sin \theta = 1\) باشد، پس \(\theta = {90^ \circ }\) می شود، پس خواهیم داشت:
\(S = \frac{1}{2} \times 50 \times 50 \times \sin \theta = \frac{1}{2} \times 50 \times 50 \times 1 = 1250\)
3 ابعاد مستطیلی با بیشترین مساحت را تعیین کنید که دو رأس آن روی محور xها و دو رأس دیگرش بالای محور xها و روی سهمی \(y = 12 - {x^2}\) باشد.
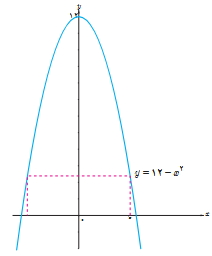
\(\begin{array}{l}S(x) = 2xy = 2x(12 - {x^2}) = 24x - 2{x^3}\\\\S'(x) = 24 - 6{x^2}\;\;\mathop \Rightarrow \limits^{S'(x) = 0} \;\;24 - 6{x^2} = 0\\\\ \Rightarrow {x^2} = 4 \Rightarrow x = 2\\\\\mathop \Rightarrow \limits^{y = 12 - {x^2}} \;\;y = 12 - 4 = 8\end{array}\)
طول مستطیل برابر با 4 و عرض آن برابر با 8 است.
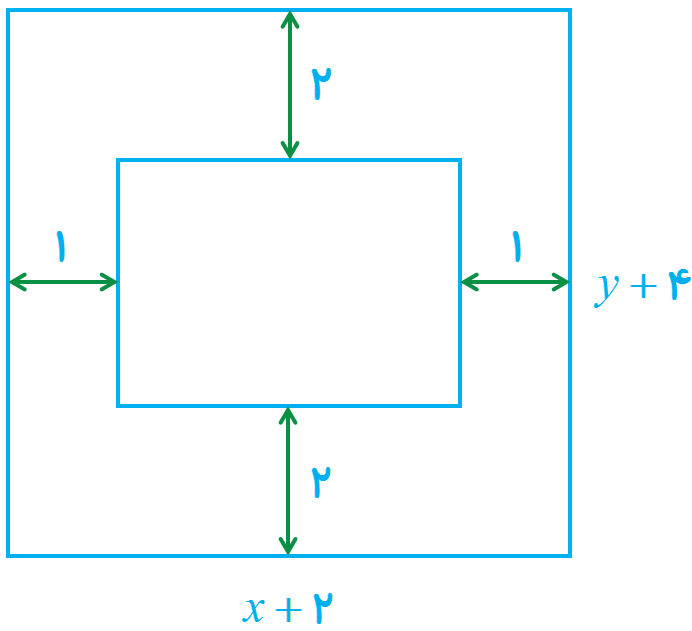
4 هر صفحهٔ مستطیل شکل از یک کتاب جیبی، شامل یک متن با مساحت ثابت 32cm2 خواهد بود. هنگام طرّاحی قطع این کتاب، لازم است حاشیه های بالا و پایینی هر صفحه 2cm و حاشیه های کناری هر کدام یک سانتی متر در نظر گرفته شوند. ابعاد صفحه را طوری تعیین کنید که مساحت هر صفحه از کتاب کمترین مقدار ممکن باشد.
\(\begin{array}{l}S(x) = (x + 2)(y + 4)\;\;\mathop \Rightarrow \limits^{xy = 32} \;\;y = \frac{{32}}{x}\\\\ \Rightarrow S(x) = 4x + \frac{{64}}{x} + 40\\\\S'(x) = 4 - \frac{{64}}{{{x^2}}} = \frac{{4{x^2} - 64}}{{{x^2}}}\\\\\mathop \Rightarrow \limits^{S'(x) = 0} \;\;4{x^2} - 64 = 0 \Rightarrow {x^2} = 16 \Rightarrow \left\{ \begin{array}{l}x = 4\\\\y = 8\end{array} \right.\end{array}\)
ابعاد جعبه برابر است با \((4 + 2 = )\;6\) و \((8 + 4 = )\;12\)
٥ آروین می خواهد به ایستگاه اتوبوسی برود که در 200 متری غرب و 60 متری شمال موقعیت فعلی او بعد از پارک قرار دارد. او می تواند با سرعت 3 متر بر ثانیه از پیاده رو کنار پارک به سمت غرب برود. همچنین، می تواند از درون پارک و تنها با سرعت 2m/s عبور کند. با توجه به شکل، مقدار x را طوری تعیین کنید که او در کمترین زمان ممکن به ایستگاه برسد.
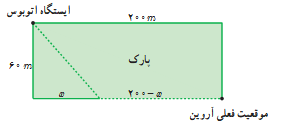
\(\begin{array}{l}\left. \begin{array}{l}{t_1} = \frac{{200 - x}}{3}\\\\{t_2} = \frac{{\sqrt {3600 + {x^2}} }}{2}\end{array} \right\}\\\\ \Rightarrow t = {t_1} + {t_2} = \frac{{200 - x}}{3} + \frac{{\sqrt {3600 + {x^2}} }}{2}\\\\ = \frac{1}{6}(400 - 2x + 3\sqrt {3600 + {x^2}} )\\\\t' = \frac{1}{6}( - 2 + 3 \times \frac{{2x}}{{2\sqrt {3600 + {x^2}} }})\;\;\mathop \Rightarrow \limits^{t' = 0} \;\;2 = \frac{{3x}}{{\sqrt {3600 + {x^2}} }}\\\\ \Rightarrow 2\sqrt {3600 + {x^2}} = 3x\\\\\mathop \Rightarrow \limits^{{{(\;)}^2}} \;\;4(3600 + {x^2}) = 9{x^2} \Rightarrow 5{x^2} = 4 \times 3600\\\\ \Rightarrow {x^2} = 2880 \Rightarrow x = 24\sqrt 5 \\\\ \Rightarrow t = \frac{1}{6}(400 - 2 \times 24\sqrt 5 + 3\sqrt {3600 + 2880} ) = 100\end{array}\)
1736019749.png)
