جواب کار در کلاس صفحه 118 درس 5 ریاضی دوازدهم تجربی (کاربرد مشتق)
تعداد بازدید : 86.5Mپاسخ کار در کلاس صفحه 118 ریاضی دوازدهم تجربی
-گام به گام کار در کلاس صفحه 118 درس کاربرد مشتق
-کار در کلاس صفحه 118 درس 5
-شما در حال مشاهده جواب کار در کلاس صفحه 118 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 می خواهیم یک قوطی فلزی استوانه ای شکل و در باز بسازیم که گنجایش آن دقیقاً یک لیتر باشد. ابعاد قوطی چقدر باشد تا مقدار فلز به کار رفته در تولید آن مینیمم شود.
حل: باید مساحت کل استوانه کمترین مقدار ممکن گردد.
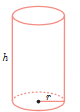
حجم استوانه 1(lit) = 1000cm2
\( \Rightarrow \pi {r^2}h = 1000\left( {c{m^2}} \right)\; \Rightarrow \;h = \frac{{1000}}{{\pi {r^2}}}\)
مساحت کل استوانه:
S = مساحت قاعده + سطح جانبی
\(\begin{array}{l}S\left( r \right) = \pi {r^2} + 2\pi rh\; \Rightarrow \;S\left( r \right) = \pi {r^2} + 2\pi r\left( {\frac{{1000}}{{\pi {r^2}}}} \right)\\\\ \Rightarrow \;S\left( r \right) = \pi {r^2} + \frac{{2000}}{r}\end{array}\)
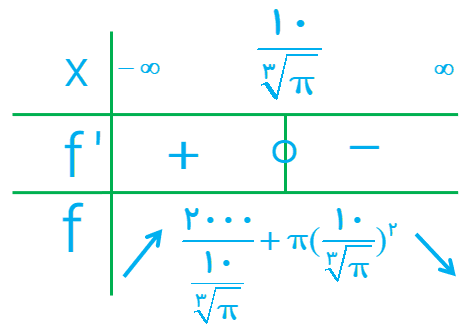
با یافتن نقطهٔ بحرانی S و تشکیل جدول تغییرات آن، مشخص کنید که به ازای چه مقداری از r، مقدار S(r) مینیمم می گردد.
\(\begin{array}{l}S(r) = 2\pi rh + \pi {r^2} = 2\pi r \times \frac{{1000}}{{\pi {r^2}}} + \pi {r^2} = \frac{{2000}}{r} + \pi {r^2}\\\\S'(r) = \frac{{ - 2000}}{{{r^2}}} + 2\pi r\;\mathop \Rightarrow \limits^{S'(r) = 0} \;\frac{{ - 2000}}{{{r^2}}} + 2\pi r = 0\\\\ \Rightarrow 2\pi {r^3} = 2000 \Rightarrow r = \frac{{10}}{{\sqrt[3]{\pi }}}\\\\S(\frac{{10}}{{\sqrt[3]{\pi }}}) = \frac{{2000}}{{\frac{{10}}{{\sqrt[3]{\pi }}}}} + \pi {(\frac{{10}}{{\sqrt[3]{\pi }}})^2}\end{array}\)
2 هزینه سوخت یک قطار در هر ساعت برای حرکت با سرعت v کیلومتر بر ساعت، برابر 320v2 تومان است. همچنین سایر هزینه ها برای هر ساعت، صرف نظر از سرعت قطار، برابر 800000 تومان می باشد. قطار با چه سرعتی حرکت کند تا هزینه آن در یک کیلومتر، کمترین مقدار ممکن باشد.
حل: اگر قطار با سرعت ثابت v کیلومتر بر ساعت حرکت کند، داریم:
هزینه t ساعت حرکت: \(C = 800000t + \left( {320{v^2}} \right)t\)
هزینه x کیلومتر حرکت: \(C = 800000\left( {\frac{x}{v}} \right) + \left( {320{v^2}} \right)\left( {\frac{x}{v}} \right)\)
هزینه 1 کیلومتر حرکت: \(C = \frac{{800000}}{v} + 320v\)
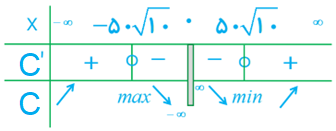
نقطهٔ بحرانی تابع C را بیابید و با تشکیل جدول تغییرات آن، سرعت بهینه را پیدا کنید.
\(\begin{array}{l}C'(v) = 0 \Rightarrow - \frac{{800,000}}{{{v^2}}} + 320 = 0\\\\ \Rightarrow {v^2} = \frac{{800,000}}{{320}} = 25,000 \Rightarrow v = \pm 50\sqrt {10} \end{array}\)
3 دو عدد حقیقی بیابید که تفاضل آنها ١٠ باشد و حاصل ضربشان کمترین مقدار ممکن گردد.
\(\begin{array}{l}x - y = 10 \Rightarrow x = 10 + y\\\\p\;(y) = xy = y\;(10 + y) = {y^2} + 10y\\\\ \Rightarrow p'\;(y) = 2y + 10\;\mathop \Rightarrow \limits^{p'\;(y) = 0} \;2y + 10 = 0\\\\ \Rightarrow \left\{ \begin{array}{l}y = - 5\\\\x = 5\end{array} \right.\end{array}\)
4 دربرخی بناهای تاریخی کشورمان پنجره هایی وجود دارد که به شکل یک مستطیل و نیم دایره ای برروی آن می باشد به طوری که قطر نیم دایره برابر با پهنای مستطیل است. اگر محیط یک چنین پنجره ای 4/5 متر باشد، ابعاد آن را طوری بیابید که بیشترین نوردهی را داشته باشد.
حل: باید مساحت پنجره بیشترین مقدار ممکن باشد.
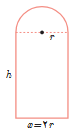
محیط = 4/5 \( \Rightarrow 2h + x + \frac{1}{2}\left( {2\pi r} \right) = \frac{9}{2}\)
\( \Rightarrow 2h + 2r + \pi r = \frac{9}{2}\; \to h = \frac{9}{2} - r - \frac{{\pi r}}{2}\)
مساحت پنجره:
S = مساحت مستطیل + مساحت نیم دایره
\(\begin{array}{l}S = xh + \frac{1}{2}\left( {\pi {r^2}} \right)\; \Rightarrow \;S\left( r \right) = 2r\left( {\frac{9}{2} - r - \frac{{\pi r}}{2}} \right) + \frac{1}{2}\pi {r^2}\\\\ \Rightarrow S\left( r \right) = - \left( {\frac{{\pi + 4}}{2}} \right){r^2} + \frac{9}{2}r\end{array}\)
با پیدا کردن نقطهٔ بحرانی S و تشکیل جدول تغییرات آن، مشخص کنید که به ازای چه مقداری از r، مقدار S(r) بیشترین مقدار ممکن می شود.
\(S'(r) = - 2(\frac{{\pi + 4}}{2})\;r + 4/5\;\;\mathop \Rightarrow \limits^{S'(r) = 0} \;\;r = \frac{{4/5}}{{\pi + 4}}\)
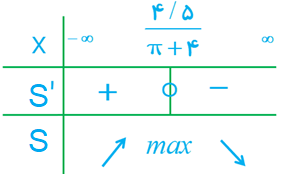
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















