جواب تمرین صفحه 44 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 78.82Mپاسخ تمرین صفحه 44 هندسه یازدهم
-گام به گام تمرین صفحه 44 درس تبدیل های هندسی و کاربردها
-تمرین صفحه 44 درس 2
-شما در حال مشاهده جواب تمرین صفحه 44 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 در حالتی که پاره خط AB در راستای عمود بر خط بازتاب قرار دارد، ثابت کنید که اگر 'A′B بازتاب AB باشد، AB و 'A′B هم اندازه اند.
طبق تعریف بازتاب:
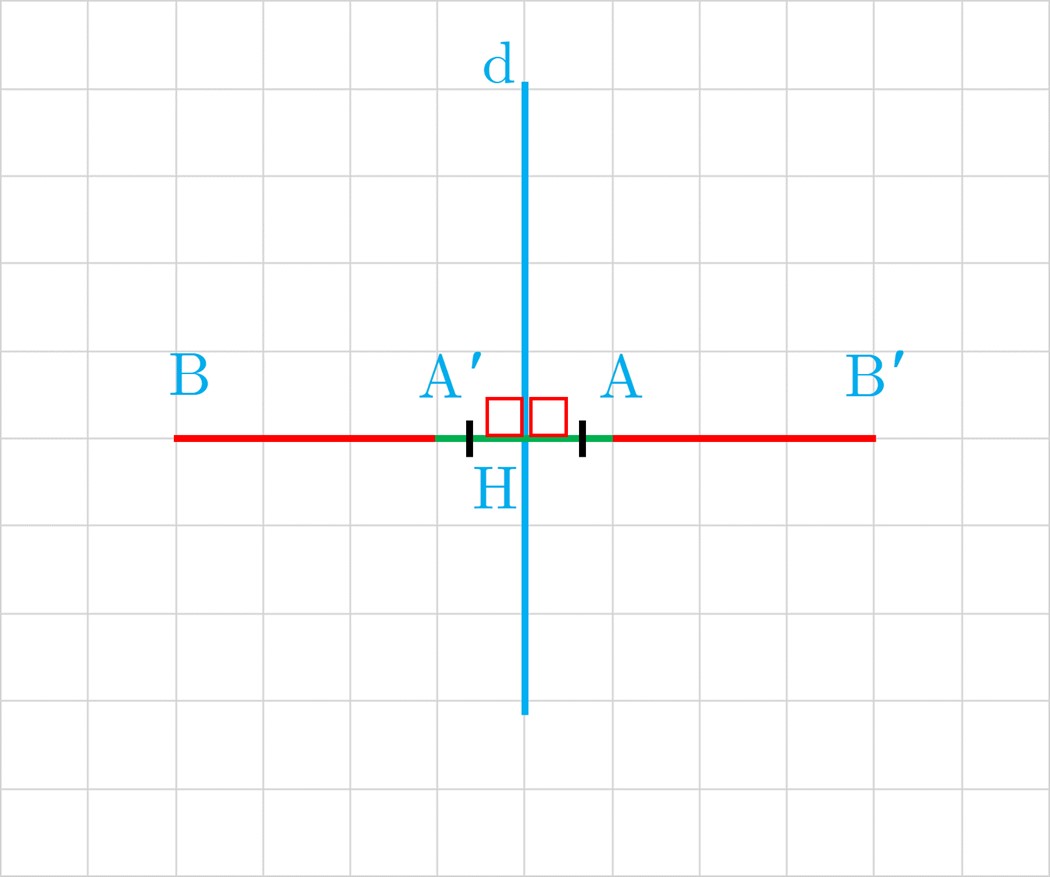
\(\begin{array}{l}BH = B'H \Rightarrow BA' + A'H = B'A + AH\\\\\mathop \Rightarrow \limits^{AH = A'H} \;\;B'A = BA'\\\\\left. \begin{array}{l}AB = AA' + A'B\\A'B' = AA' + B'A\\B'A = BA'\end{array} \right\} \Rightarrow AB = A'B'\end{array}\)
2 در شکل زیر چهار ضلعی 'A′B′C′D تصویر چهارضلعی محدب ABCD تحت بازتاب است. در شکل اولیه وقتی به ترتیب از A به C، B و D می رویم، جهت حرکت، موافق جهت حرکت عقربه های ساعت است. جهت حرکت در بازتاب این نقاط چگونه است؟ آیا می توان گفت بازتاب، جهت شکل را حفظ می کند؟
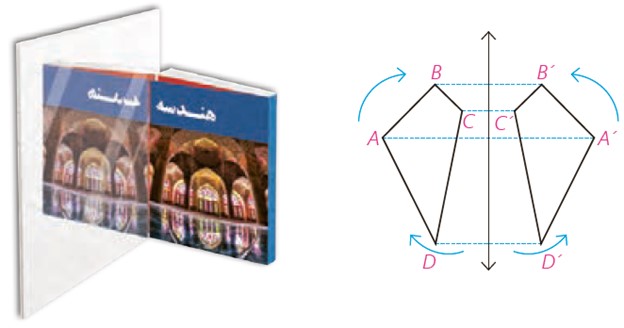
جهت حرکت در بازتاب این نقاط خلاف جهت حرکت عقربه های ساعت است؛ خیر نمی توان گفت بازتاب جهت شکل را حفظ می کند.
3 به سؤالات زیر پاسخ دهید.
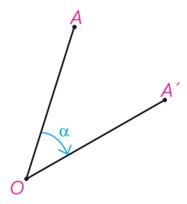
الف در شکل مقابل نقطه ′A دوران یافته نقطه A در دوران به مرکز O و زاویه α است. نشان دهید عمودمنصف ′AA از نقطه O می گذرد.
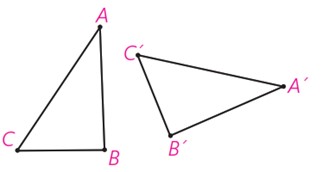
ب اگر بدانیم مثلث A’B’C’ دوران یافته مثلث ABC است، چگونه می توان مرکز دوران را مشخص کرد؟
الف
بنا بر تعریف دوران OA=OA’ ، در نتیجه نقطه O به یک فاصله از نقاط A و A’ قرار دارد، در نتیجه بنا بر تعریف عمودمنصف، نقطه O بر روی عمودمنصف پاره خط AA’ قرار دارد.
ب
می دانیم که مرکز دوران بر روی عمودمنصف پاره خط تشکیل شده از رئوس نقطه و تصویر همان نقطه قرار دارد. حال اگر این عمودمنصف ها را رسم کنیم، این خط ها یکدیگر را در مرکز دوران قطع خواهند کرد.
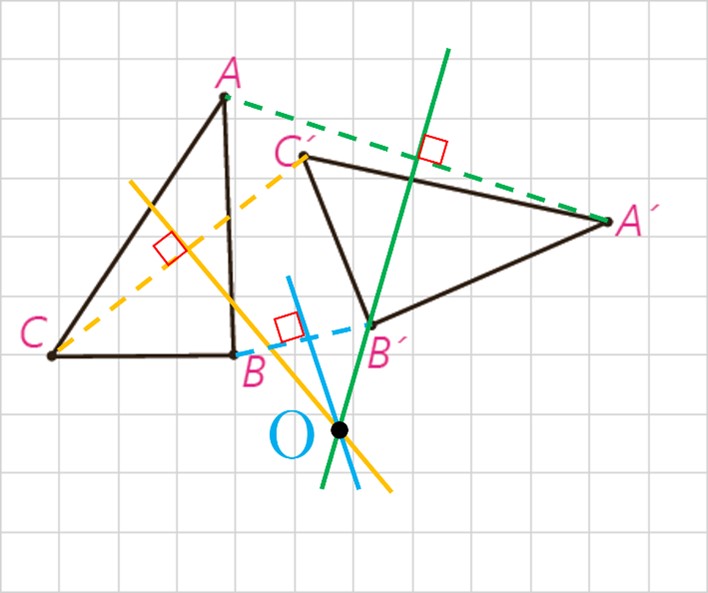
4 در شکل، d1 به موازات d2 و به فاصله m از آن قرار دارد و مثلث 'A’B’C بازتاب مثلث ABC نسبت به خط d1 است. بازتاب مثلث 'A’B’C را نسبت به خط d2 رسم کنید و آن را مثلث ”A”B”C بنامید.
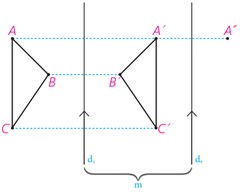
الف نشان دهید: AA″=2m
ب اندازه ″BB و ″CC چقدر است؟
پ با چه تبدیلی می توان مثلث ”A”B”C را تصویر مثلث ABC دانست؟ چه نتیجه ای می گیرید؟
الف
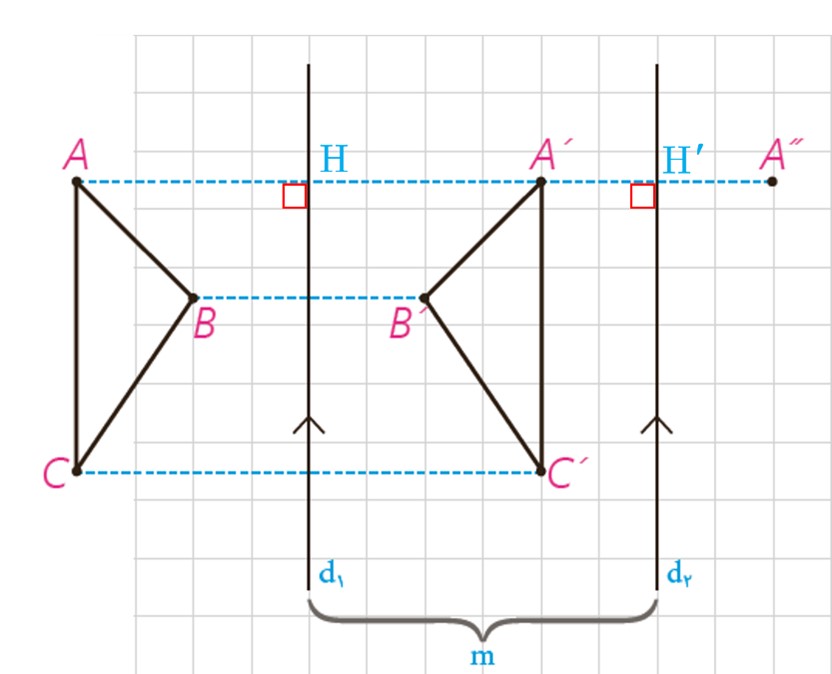
\(\begin{array}{l}AA'' = AH + HA' + A'H' + H'A''\\\\\mathop \Rightarrow \limits_{A'H' = H'A''}^{AH = HA'} \;\;2HA' + 2A'H'\\\\ \Rightarrow AA'' = 2\left( {HA' + A'H'} \right) \Rightarrow AA'' = 2m\end{array}\)
ب
بنا بر اثبات قسمت (الف) به روش مشابه نتیجه می گیریم که: \(BB'' = CC'' = 2m\)
پ
با انتقالی تحت بردار انتقالی که اندازه آن دو برابر فاصله بین دو خط بازتاب d1 و d2 یعنی m2 و راستای آن عمود بر این دو خط است، می توان مثلث \(A''\mathop {B''}\limits^\Delta C''\) را تصویر مثلث \(A\mathop B\limits^\Delta C\) دانست.
نتیجه می گیریم ترکیب دو بازتابی که محورهای بازتاب، موازی یکدیگر هستند یک انتقال است.
5 در شکل، دو خط d1 و d2 با زاویه θ یکدیگر را قطع کرده اند. مثلث 'A’B’C بازتاب مثلث ABC نسبت به خط d1 است. بازتاب مثلث 'A’B’C را نسبت به خط d2 رسم کنید و آن را ”A”B”C بنامید.
الف نشان دهید: \(\widehat {AOA''} = 2\theta \)
ب اندازه \(\widehat {COC''}\) و \(\widehat {BOB''}\) چقدر است؟
پ با چه تبدیلی می توان مثلث ”A”B”C را تصویر ABC دانست؟ چه نتیجه ای می گیرید؟
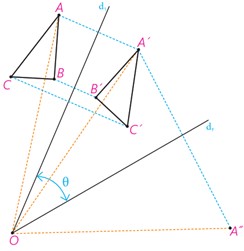
الف
خط d1 محور بازتاب است، پس نیمساز زاویه AOA’ است؛ یعنی: \({\widehat O_1} = {\widehat O_2}\)
خط d2 محور بازتاب است، پس نیمساز زاویه A’OA” است؛ یعنی: \({\widehat O_3} = {\widehat O_4}\)

\(\begin{array}{l}\widehat {AOA''} = {\widehat O_1} + {\widehat O_2} + {\widehat O_3} + {\widehat O_4}\;\\\\\mathop \Rightarrow \limits_{{{\widehat O}_3} = {{\widehat O}_4}}^{{{\widehat O}_1} = {{\widehat O}_2}} \widehat {AOA''} = 2{\widehat O_2} + 2{\widehat O_3}\\\\ \Rightarrow \widehat {AOA''} = 2({\widehat O_2} + {\widehat O_3}) \Rightarrow \widehat {AOA''} = 2\theta \end{array}\)
ب
بنا بر اثبات قسمت (الف) بطور مشابه: \(\widehat {BOB''} = \widehat {COC''} = 2\theta \)
پ
با دورانی به مرکز O نقطه برخورد دو خط بازتاب d1 و d2 و زاویه ای به اندازه رو برابر زاویه بین دو خط (\(2θ\)) می توان مثلث A”B”C” را تصویر مثلث ABC دانست.
نتیجه می گیریم که ترکیب دو بازتاب که محورهای بازتاب متقاطع باشند، یک دوران است.
6 نقطه A به فاصله \(2\sqrt 6 \) از خط d قرار دارد. تصویر نقطه A را تحت بازتاب نسبت به خط d، نقطه ′A می نامیم. نقطه A را حول نقطه ′A به اندازه 120 درجه دوران می دهیم تا نقطه ′′A حاصل شود. طول پاره خط ′′AA را محاسبه کنید.
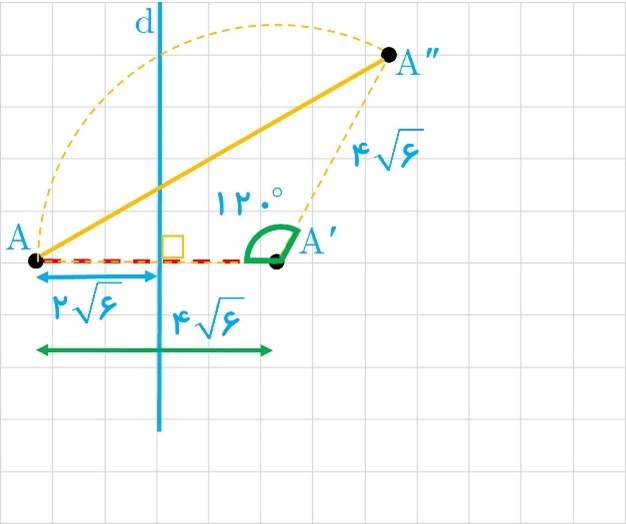
\(\begin{array}{l}AA'' = \sqrt {A{{A'}^2} + A'{{A''}^2} - 2AA' \cdot A'A''\sin {{120}^ \circ }} \\\\ = \sqrt {{{(4\sqrt 6 )}^2} + {{(4\sqrt 6 )}^2} - 2(4\sqrt 6 )(4\sqrt 6 )(\frac{{\sqrt 3 }}{2})} = 12\sqrt 2 \end{array}\)
7 نقطه ′A تصویر نقطه A در بازتاب نسبت به خط l است. اگر AA′=16 و نقطه O روی خط l و OA=10 باشد، فاصله نقطه A از خط ′OA چقدر است؟
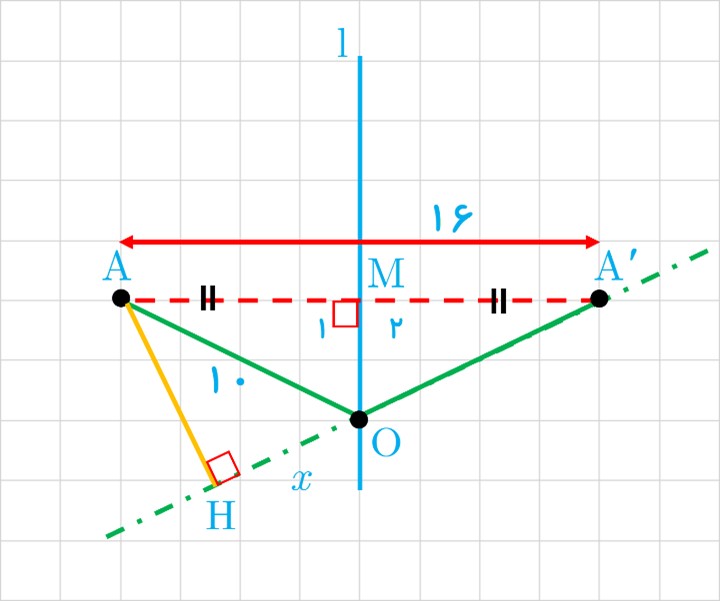
\(\left. \begin{array}{l}AM = A'M\\{\widehat M_1} = {\widehat M_2} = {90^ \circ }\\OM = common\end{array} \right\} \Rightarrow A\mathop O\limits^\Delta M \cong A'\mathop O\limits^\Delta M \Rightarrow OA = OA' = 10\)
Common = مشترک
\(\begin{array}{l}A{H^2} = A{O^2} - O{H^2} = AA'{\,^2} - A{H^2}\\\\ \Rightarrow {10^2} - {x^2} = {16^2} + {(10 + x)^2}\\\\100 - {x^2} = 256 - 100 - 20x - {x^2}\\\\ \Rightarrow 20x = 56 \Rightarrow x = \frac{{56}}{{20}} = 2/8\\\\A{H^2} = 100 - {x^2} = 100 - 2/{8^2} = 92/16\\\\ \Rightarrow AH = \sqrt {92/16} \simeq 9/6\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















