جواب مسائلی برای علاقه مندان صفحه 57 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 84.75Mپاسخ مسائلی برای علاقه مندان صفحه 57 هندسه یازدهم
-گام به گام مسائلی برای علاقه مندان صفحه 57 درس تبدیل های هندسی و کاربردها
-مسائلی برای علاقه مندان صفحه 57 درس 2
-شما در حال مشاهده جواب مسائلی برای علاقه مندان صفحه 57 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1
الف با تکمیل جدول زیر تعداد تبدیل های تقارنی n ضلعی منتظم را مشخص کنید.
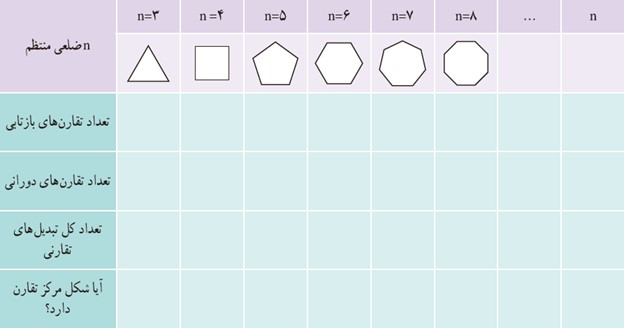
ب n ضلعی منتظم در چه صورتی مرکز تقارن دارد؟
پ الگویی برای پیدا کردن زاویه های دوران در تقارن های دورانی یک n ضلعی منتظم ارائه کنید.
الف
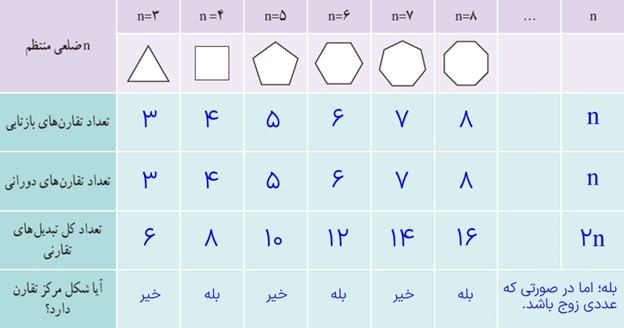
ب
در صورتی که عدد زوج باشد.
دلیل:
مرکز تقارن نقطهای است که اگر شکل را به اندازهی 180 درجه حول آن دوران دهیم، شکل بر روی خودش منطبق میشود. در یک n ضلعی منتظم، زاویههای دوران برابر با مضربهای \(\frac{{{{360}^ \circ }}}{n}\) هستند.
برای اینکه دوران 180 درجه یکی از این تقارنها باشد، باید n زوج باشد تا حاصل تقسیم \(\frac{{{{360}^ \circ }}}{n}\) عددی باشد که مضرب صحیحی از آن برابر با ۱۸۰ شود؛ یعنی \(n = 2k\,\,\,,\,\,\,k \in \mathbb{N}\)
پ
الگوی زاویههای دوران:
برای پیدا کردن تمام زاویههای دوران در تقارنهای دورانی یک n ضلعی منتظم، از الگوی زیر استفاده میکنیم:
ا) ابتدا کوچکترین زاویه دوران را محاسبه می کنیم. این مقدار برابر خواهد بود با:
\(\alpha = \frac{{{{360}^ \circ }}}{n}\)
2) حال باقی زوایای دوران را محاسبه می کنیم. این زاویه ها، مضرب های طبیعی از کوچکترین زاویه دوران خواهد بود. این زاویا از رابطه زیر بدست می آیند:
\(\theta = k \times \alpha \,\,\,\,\,,\,\,\,\,\,k = 1\,,\,2\,,\,3\,,\,...\,,\,n\)
مثال:
به عنوان مثال، می خواهیم زاویه های دوران برای یک شش ضلعی متنظم را پیدا کنیم:
1) ابتدا کوچکترین زاویه دوران را پیدا می کنیم. طبق رابطه ی زیر، این مقدار بدست می آید:
\(\alpha = \frac{{{{360}^ \circ }}}{6} = {60^ \circ }\)
2) حال باقی زاویای دوران را برای شش ضلعی منتظم بدست می آوریم:
\(\begin{array}{l}n = 6\\\\\theta = k \times {60^ \circ }\,\,\,\,\,,\,\,\,\,\,k = 1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\\\\\theta = {60^ \circ }\,,\,{120^ \circ }\,,\,{180^ \circ }\,,\,{240^ \circ }\,,\,{300^ \circ }\,,\,{360^ \circ }\end{array}\)
2 تقارن های خطی و دورانی متوازی الاضلاع، مستطیل، لوزی، مثلث متساوی الساقین و ذوزنقه متساوی الساقین را مشخص کنید و در جدولی بنویسید.
کدام یک از این شکل های هندسی، مرکز تقارن دارند؟
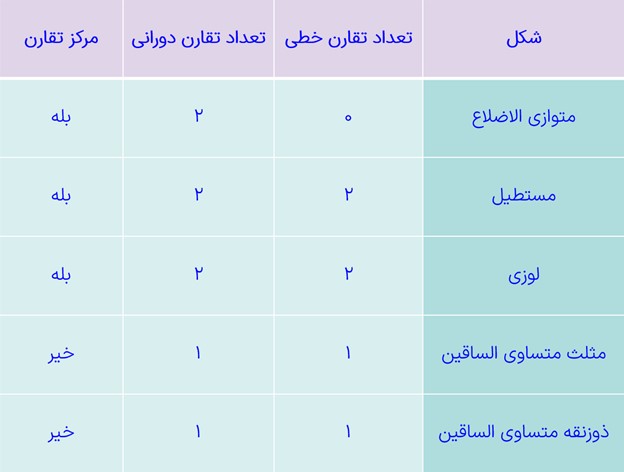
از بین این اشکال، متوازیالاضلاع، مستطیل و لوزی مرکز تقارن دارند. مرکز تقارن در این سه شکل، محل برخورد قطرهایشان است. توجه داشته باشیم که هر شکل حداقل یک تقارن دورانی 360 درجه که همان «تقارن همانی» هست را دارد. یعنی با دوران دادن شکل به اندازه زاویه 360 درجه، شکل بر روی خودش قرار می گیرد.
3
الف شکلی رسم کنید که خط بازتاب داشته باشد، ولی مرکز تقارن نداشته باشد (یعنی تقارن خطی داشته باشد، اما تقارن دورانی غیرهمانی نداشته باشد.)
ب شکلی رسم کنید که مرکز تقارن داشته باشد، ولی خط بازتاب نداشته باشد (یعنی تقارن دورانی غیرهمانی داشته باشد، اما تقارن خطی نداشته باشد.)
الف
یک مثلث متساویالساقین یا شکل یک قلب؛ این اشکال یک محور تقارن عمودی دارند اما با دوران ۱۸۰ درجه بر خود منطبق نمیشوند.
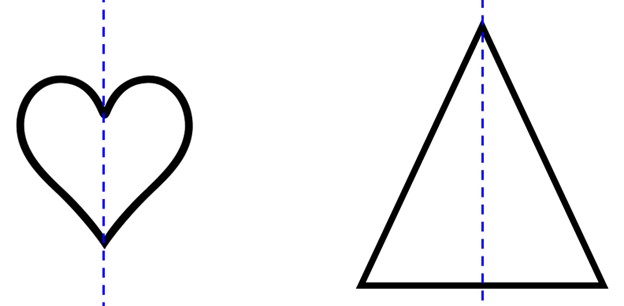
ب
متوازی الاضلاعی که مستطیل یا لوزی نباشد؛ این شکل با دوران ۱۸۰ درجه حول نقطه مرکزی خود بر خودش منطبق میشود (مرکز تقارن دارد)، اما هیچ خط تقارنی ندارد. حروف انگلیسی مانند S یا Z یا N نیز همین ویژگی را دارند.
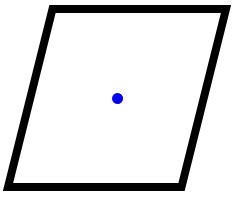
4 نشان دهید اگر شکلی دو خط بازتاب عمود بر هم داشته باشد، محل تلاقی این دو خط، مرکز تقارن شکل است (در واقع هر شکل که دارای دو تقارن بازتابی باشد که دو خط بازتاب آن بر هم عمود باشند، دارای تقارن دورانی است.)
این موضوع را میتوانیم با یک کاغذ انجام دهیم!
یک مستطیل کاغذی بردارید. (مثل یک ورق A4). مستطیل خودش دو خط تقارن عمود بر هم دارد: یکی خطی که از وسط طول آن میگذرد و دیگری خطی که از وسط عرض آن میگذرد. محل برخورد این دو خط، دقیقاً مرکز کاغذ است.

در گوشهی بالا-چپ کاغذ، یک شکل کوچک و نامتقارن بکشید. مثلاً حرف انگلیسی F.

تای اول (بازتاب اول): کاغذ را از روی خط تقارن افقی تا بزنید. شکل F شما به قسمت پایین کاغذ منتقل میشود. حالا کاغذ را باز کنید. الان یک F در بالا و یک F برعکس در پایین دارید.
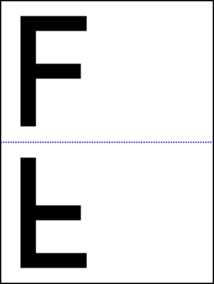
تای دوم (بازتاب دوم): حالا کاغذ را از روی خط تقارن عمودی تا بزنید. آن F برعکسی که در مرحله قبل در پایین کاغذ ایجاد شده بود، به قسمت پایین-راست کاغذ منتقل میشود.
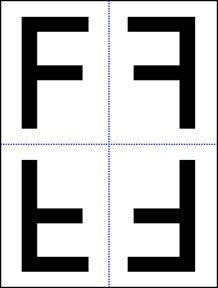
نتیجهگیری نهایی:
حالا کاغذ را کاملاً باز کنید و به حرف F اصلی (در بالا-چپ) و حرف F نهایی (در پایین-راست) نگاه کنید. چه رابطهای بین آنها وجود دارد؟
میبینید که حرف F نهایی، دقیقاً همان حرف F اصلی است که یک چرخش ۱۸۰ درجه (نیم دور) حول مرکز کاغذ داشته است!
این آزمایش ساده نشان میدهد که:
وقتی یک شکل را دو بار پشت سر هم حول دو خط عمود بر هم بازتاب میدهیم، نتیجهاش مثل این است که شکل را ۱۸۰ درجه حول نقطهی مرکزی چرخانده باشیم. برای همین، آن نقطهی مرکزی، مرکز تقارن شکل است.
شکل نهایی که دو خط بازتاب عمود بر هم داشته باشد، به صورت زیر می باشد:

5 جدول زیر را کامل کنید.
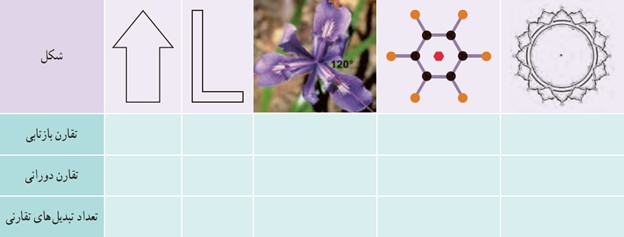
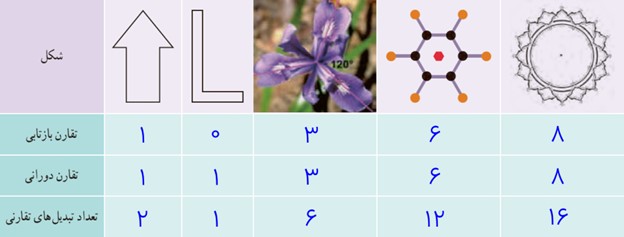
توجه:
هر شکل حداقل یک تقارن دورانی 360 درجه که همان «تقارن همانی» هست را دارد. یعنی با دوران دادن شکل به اندازه زاویه 360 درجه، شکل بر روی خودش قرار می گیرد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















