1736019749.png)
جواب سؤال متن صفحه 51 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 78.82Mپاسخ سؤال متن صفحه 51 هندسه یازدهم
-گام به گام سؤال متن صفحه 51 درس تبدیل های هندسی و کاربردها
-سؤال متن صفحه 51 درس 2
-شما در حال مشاهده جواب سؤال متن صفحه 51 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 می خواهیم کیکی به شکل زیر را به طور مساوی بین دو نفر تقسیم کنیم. نمای بالای کیک از مربع BCDE و کمان AE از یک دایره تشکیل شده است به طوری که A و B و E روی یگ خط هستند.
اگر نمای بالای کیک به شکل روبه رو بود، تقسیم آن کار ساده ای بود؛ چرا که می توانستیم از روی خط بازتاب m کیک را برش بزنیم و آن را به دو نیمهٔ مساوی تقسیم کنیم.
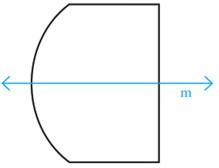
این شکل، راه ساده ای برای برش زدن کیک و تقسیم آن به دو سهم برابر ارائه می کند. توضیح دهید که بازتاب به حل این مسئله چه کمکی کرده است.
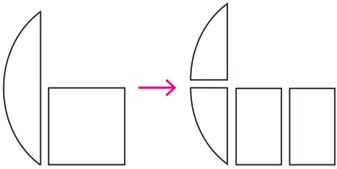
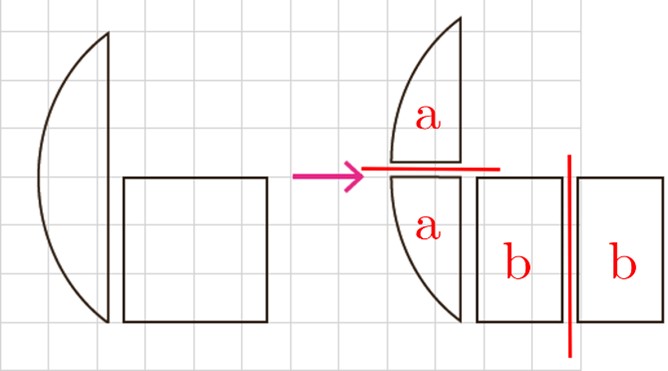
شکل های a نسبت به محور بازتاب قرینه اند، پس هم اندازه اند.
همچنین شکل های b هم نسبت به محور بازتاب خود قرینه اند و در نتیجه هم اندازه اند. حال به هر نفر یک شکل a و یک شکل b می دهیم.
2 یکی از کاربردهای بازتاب، حل مسائلی است که به مسائل هم پیرامونی یا هم محیطی معروف است. در این گونه مسائل، هدف این است که بدون اینکه محیط یک چند ضلعی تغییر کند، مساحت آن چند ضلعی را تغییر دهیم.
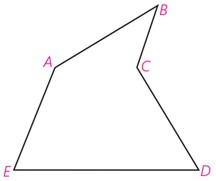
برای مثال فرض کنید که زمینی به شکل چندضلعی ABCDE داریم که دور آن را حصار کشیده ایم. حال می خواهیم با ثابت نگهداشتن محیط و ثابت نگهداشتن تعداد اضلاع چند ضلعی، بدون اینکه اندازه حصار کشی تغییر کند، مساحت زمین را افزایش دهیم.
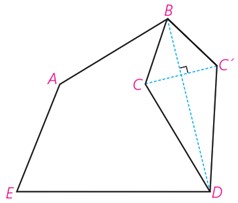
به کمک این تصویر توضیح دهید که این عمل را چگونه می توان انجام داد.
چرا محیط چندضلعی ABCDE با محیط چندضلعی ABC’DE یکی است؟
در شکل از نقطه B به D وصل می کنیم. سپس آن را به عنوان محور بازتاب در نظر می گیریم. تصویر نقاط B ، C و D را نسبت به این محور بدست می آوریم. واضح است که تصویر نقاط B و D روی خودشان منطبق است ولی تصویر نقطه C ، نقطه C’ خواهد بود.
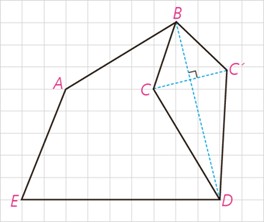
با توجه به اینکه بازتاب یک تبدیل طولپاست، پس داریم:
\(\begin{array}{l}BC = BC'\;\;,\;\;CD = C'D\\\\{P_{ABCDE}} = AB + BC + CD + DE + EA\\\\\mathop \Rightarrow \limits_{CD = C'D}^{BC = BC'} \;\;{P_{ABCDE}} = AB + BC' + C'D + DE + EA\\\\ \Rightarrow {P_{ABCDE}} = {P_{ABC'DE}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
