جواب فعّالیت صفحه 44 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 84.75Mپاسخ فعّالیت صفحه 44 هندسه یازدهم
-گام به گام فعّالیت صفحه 44 درس تبدیل های هندسی و کاربردها
-فعّالیت صفحه 44 درس 2
-شما در حال مشاهده جواب فعّالیت صفحه 44 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 این دو شکل، نمونه ای از تجانس را نشان می دهند که در یکی، مرکز تجانس داخل شکل اولیه و در دیگری خارج آن در نظر گرفته شده است.
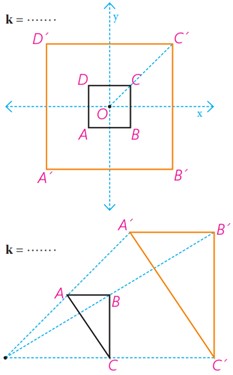
الف به کمک صفحه شطرنجی در هر شکل نسبت تجانس را مشخص کنید.
ب آیا تجانس طولپاست؟ چرا؟
پ در این شکل ها، طول هر پاره خط را با طول تصویر آن مقایسه کنید. به چه نتیجه ای می توان رسید؟
ت مساحت هر شکل را با مساحت تصویر آن مقایسه کنید. چه نسبتی با هم دارند؟
الف
با توجه به تعریف تجانس نقاط B و B’ در یک طرف O قرار دارند، پس 0<k در نتیجه:
\(OB' = k \cdot OB \Rightarrow k = \frac{{OB'}}{{OB}} = \frac{{3\sqrt 2 }}{{\sqrt 2 }} \Rightarrow k = 3\)
\(OC' = k \cdot OC \Rightarrow k = \frac{{OC'}}{{OC}} = \frac{{10}}{5} \Rightarrow k = 2\)
ب
خیر؛ زیرا اندازه پاره خط را حفظ نمی کند.
پ
در مربع:
\(\begin{array}{l}A'B' = 3AB\quad ,\quad B'C' = 3BC\quad ,\\C'D' = 3CD\quad ,\quad D'A' = 3DA\end{array}\)
طول تصویر هر پاره خط 3 برابر شده و در واقع این عدد همان نسبت تجانس است. همچنین محیط شکل 3 برابر می شود.
در مثلث:
\(\begin{array}{l}A'B' = 2AB\quad ,\quad B'C' = 3BC\\\\AC = \sqrt {4 + 9} = \sqrt {13} \quad ,\\\\A'C' = \sqrt {16 + 36} = \sqrt {52} = 2\sqrt {13} \\\\ \Rightarrow A'C' = 2AC\end{array}\)
طول تصویر هر پاره خط 2 برابر شده و در واقع این عدد همان نسبت تجانس است. همچنین محیط شکل 2 برابر می شود.
ت
در مربع:
\(\frac{{{S_{A'\mathop {B'C'}\limits^{} D'}}}}{{{S_{A\mathop {BC}\limits^{} D}}}} = \frac{{36}}{4} = 9 = {3^2}\)
در مثلث:
\(\frac{{{S_{A'\mathop {B'}\limits^\Delta C'}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{{\frac{1}{2} \times 4 \times 6}}{{\frac{1}{2} \times 2 \times 3}} = 4 = {2^2}\)
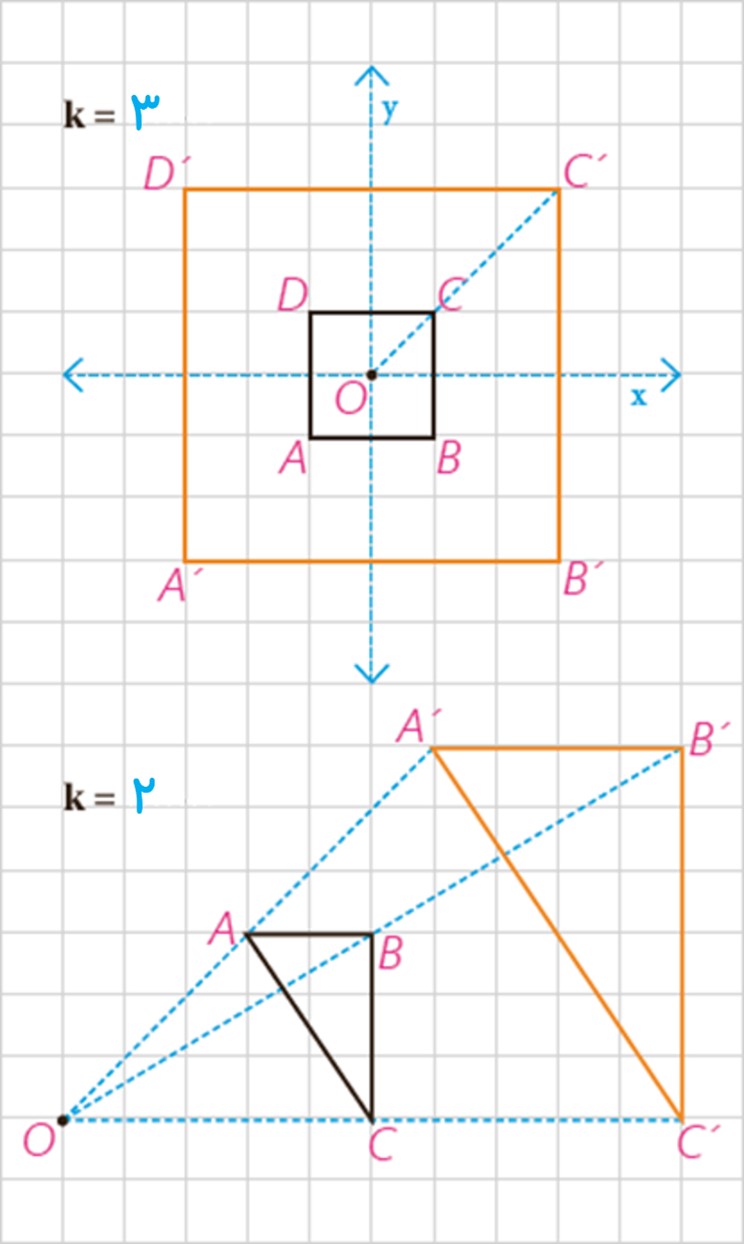
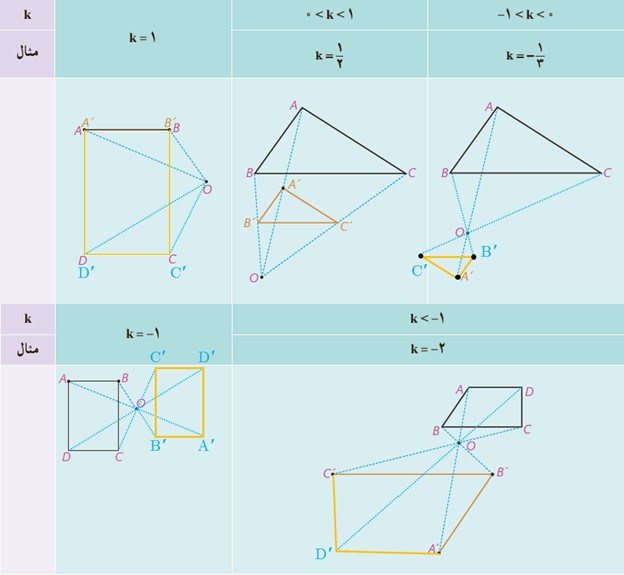
2 در هر دو حالت فوق، نسبت تجانس مقداری بیش از یک است؛ به عبارتی:. k<1 حال مسئله را برای مقادیر مختلف k بررسی می کنیم.
الف در هر حالت مراحل باقیمانده را کامل کنید.
ب با توجه به تصاویر صفحه قبل به طور شهودی، درستی یا نادرستی هر عبارت را مشخص کنید:
پ شرط اینکه تجانس طولپا باشد، این است که .................
ت خطوطی که هر نقطه را به تصویر آن نظیر می کند، یعنی خطوط 'BB'، AA و ... نسبت به هم چه وضعی دارند؟
ث اگر مثلث 'A’B’C مجانس مثلث ABC باشد، مرکز تجانس را چگونه می توان پیدا کرد؟
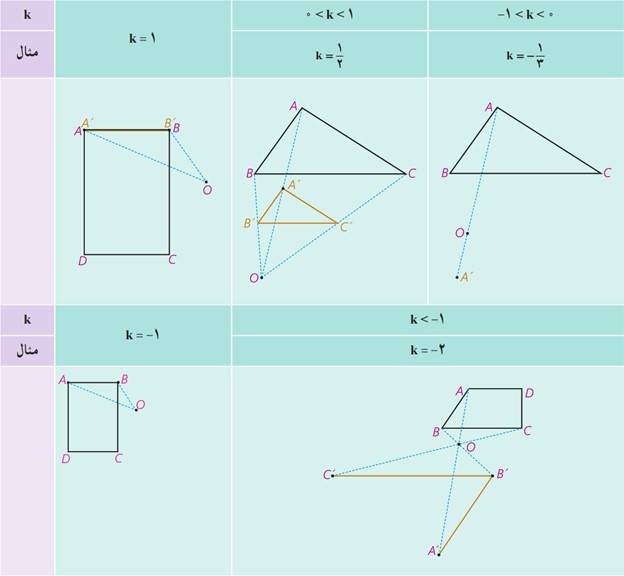
در تجانس به مرکز O و نسبت k :
اگر k<0 تجانس را، تجانس مستقیم می نامیم.
اگر k>0 تجانس را تجانس معکوس می نامیم.
اگر \(|k|<1 \) تصویر شکل .......... می شود و آن را انقباض می نامیم.
اگر ........... تصویر شکل، بزرگتر می شود و آن را انبساط می نامیم.
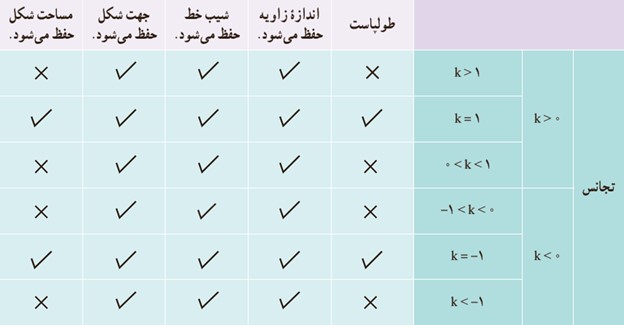
حال که به طور شهودی با تجانس و چگونگی عملکرد آن روی شکل های هندسی آشنا شدید با استدلال دقیق تری ثابت خواهیم کرد که تجانس تبدیلی است که در حالت کلی شیب خط و اندازه زاویه را حفظ می کند.
الف
ب
پ
شرط اینکه تجانس طولپا باشد، این است که \(\left| k \right| = 1 \Rightarrow k = \pm 1\)
ت
این خطوط در مرکز تجانس یعنی نقطه O همرسند.
ث
خطوط AA’ و BB’ و CC’ را رسم می کنیم. چون این نقاط در مرکز تجانس یعنی O همرسند، محل تقاطع این خطوط مرکز تجانس خواهد بود.
اگر |k|<1 تصویر شکل ...کوچکتر... می شود و آن را انقباض می نامیم.
اگر ...بزرگتر... تصویر شکل، بزرگتر می شود و آن را انبساط می نامیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















