جواب تمرین صفحه 123 درس 7 ریاضی نهم (عبارت های گویا)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 123 ریاضی نهم
-گام به گام تمرین صفحه 123 درس عبارت های گویا
-تمرین صفحه 123 درس 7
-شما در حال مشاهده جواب تمرین صفحه 123 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 ضرب و تقسیم های زیر را انجام دهید. (در همهٔ تمرین ها مخرج کسرها مخالف صفر فرض شده است)
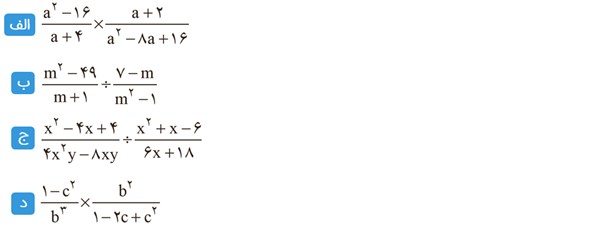
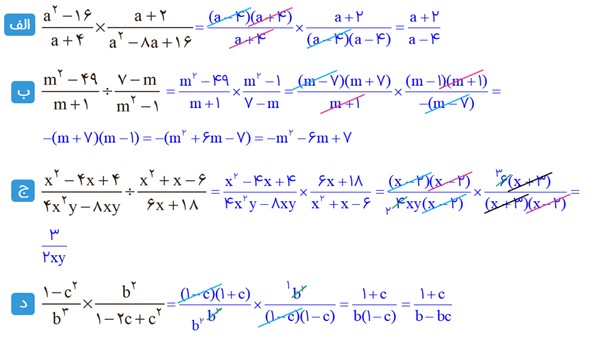
2 جمع و تفریق های زیر را انجام دهید.
\(\frac{x}{{{x^2} + {y^2}}} - \frac{{y{{(x - y)}^2}}}{{{x^4} - {y^4}}}\) الف
\(\frac{{x + 7}}{{ax - bx}} + \frac{{y + 9}}{{by - ay}}\) ب
\(\frac{{{a^2} - {b^2}}}{{a - b}} - \frac{{{a^3} - {b^3}}}{{{a^2} - {b^2}}}\) ج
\(\frac{{4 + {x^2} - 2x}}{{2 + x}} - 2 - x\)د
\(\frac{x}{{{x^2} + {y^2}}} - \frac{{y{{(x - y)}^2}}}{{{x^4} - {y^4}}} = \) الف
\(\begin{array}{l}\frac{x}{{{x^2} + {y^2}}} - \frac{{y(x - y)(x - y)}}{{({x^2} + {y^2})(x + y)(x - y)}} = \\\\\frac{x}{{{x^2} + {y^2}}} - \frac{{y(x - y)}}{{({x^2} + {y^2})(x + y)}} = \\\\\frac{{x(x + y) - y(x - y)}}{{({x^2} + {y^2})(x + y)}} = \\\\\frac{{{x^2} + xy - xy + {y^2}}}{{({x^2} + {y^2})(x + y)}} = \\\\\frac{{{x^2} + {y^2}}}{{({x^2} + {y^2})(x + y)}} = \\\\\frac{1}{{x + y}}\end{array}\)
\(\frac{{x + 7}}{{ax - bx}} + \frac{{y + 9}}{{by - ay}} = \) ب
\(\begin{array}{l}\frac{{x + 7}}{{(a - b)x}} + \frac{{y + 9}}{{ - (a - b)y}} = \\\\\frac{{(x + 7) \times ( - y) + x(y + 9)}}{{ - (a - b)xy}} = \\\\\frac{{ - xy - 7y + xy + 9x}}{{ - (a - b)xy}} = \\\\\frac{{9x - 7y}}{{bxy - axy}}\end{array}\)
\(\frac{{{a^2} - {b^2}}}{{a - b}} - \frac{{{a^3} - {b^3}}}{{{a^2} - {b^2}}} = \) ج
\(\begin{array}{l}\frac{{(a - b)(a + b)}}{{a - b}} - \frac{{(a - b)({a^2} + ab + {b^2})}}{{(a - b)(a + b)}} = \\\\a + b - \frac{{{a^2} + ab + {b^2}}}{{a + b}} = \\\\\frac{{{{(a + b)}^2} - ({a^2} + ab + {b^2})}}{{a + b}} = \\\\\frac{{({a^2} + 2ab + {b^2}) - ({a^2} + ab + {b^2})}}{{a + b}} = \\\\\frac{{{a^2} + 2ab + {b^2} - {a^2} - ab - {b^2}}}{{a + b}} = \\\\\frac{{ab}}{{a + b}}\end{array}\)
\(\frac{{4 + {x^2} - 2x}}{{2 + x}} - 2 - x = \) د
\(\begin{array}{l}\frac{{4 + {x^2} - 2x}}{{2 + x}} - (2 + x) = \\\\\frac{{4 + {x^2} - 2x - {{(2 + x)}^2}}}{{2 + x}} = \\\\\frac{{4 + {x^2} - 2x - (4 + 4x + {x^2})}}{{2 + x}} = \\\\\frac{{4 + {x^2} - 2x - 4 - 4x - {x^2}}}{{2 + x}} = \\\\\frac{{ - 6x}}{{2 + x}}\end{array}\)
3 فقط یکی از عبارت های گویای زیر قابل ساده شدن است؛ آن را مشخص و ساده کنید.
\(\begin{array}{l}\frac{{{a^2} + 5}}{{{a^2}}}\;\;,\;\;\frac{{{a^2} + 3}}{3}\\\\\frac{{{a^2} + {b^2}}}{{{a^2}}}\;\;,\;\;\frac{{{a^2} - 5a}}{a}\end{array}\)
عبارت های زیر قابل ساده شدن نیستند:
\(\begin{array}{l}\frac{{{a^2} + 5}}{{{a^2}}}\\\\\frac{{{a^2} + 3}}{3}\\\\\frac{{{a^2} + {b^2}}}{{{a^2}}}\end{array}\)
تنها عبارتی که قابل ساده شدن می باشد، عبارت زیر هست:
\(\frac{{{a^2} - 5a}}{a} = \frac{{a(a - 5)}}{a} = a - 5\)
4 از میان عبارت های زیر، هر کدام را که مساوی عبارت \(\frac{x}{y}\) است، معلوم کنید.
\(\frac{{x + 3}}{{y + 3}}\) الف
\(\frac{{3 - x}}{{3 - y}}\) ب
\(\frac{{3x}}{{3y}}\) ج
\(\frac{{{x^3}}}{{{y^3}}}\) د
\(\frac{{{a^3}x}}{{{a^3}y}}\) هـ
عبارت های (ج) و (هـ) مساوی عبارت \(\frac{x}{y}\) می باشند:
\(\frac{{3x}}{{3y}} = \frac{{\not 3 \times x}}{{\not 3 \times y}} = \frac{x}{y}\) ج
\(\frac{{{a^3}x}}{{{a^3}y}} = \frac{{{a^3} \times x}}{{{a^3} \times y}} = \frac{x}{y}\) هـ
5 عبارت \(\frac{{ - x + 3}}{{x + 5}}\) با کدام یک از عبارت های زیر برابر است؟
\( - \frac{{x + 3}}{{x + 5}}\) الف
\( - \frac{{x - 3}}{{x + 5}}\) ب
\(\frac{{x - 3}}{{x + 5}}\) ج
\( - \frac{{3 - x}}{{x + 5}}\) د
بایستی تک تک عبارت ها را بررسی کنیم:
\( - \frac{{x + 3}}{{x + 5}} = \frac{{ - (x + 3)}}{{x + 5}} = \frac{{ - x - 3}}{{x + 5}}\) الف
برابر نیست
\( - \frac{{x - 3}}{{x + 5}} = \frac{{ - (x - 3)}}{{x + 5}} = \frac{{ - x + 3}}{{x + 5}}\) ب
برابر می باشد
\(\frac{{x - 3}}{{x + 5}}\) ج
برابر نیست
\( - \frac{{3 - x}}{{x + 5}} = \frac{{ - (3 - x)}}{{x + 5}} = \frac{{x - 3}}{{x + 5}}\) د
برابر نیست
6 کدام یک از عبارت های زیر به درستی ساده شده است؟
\(\frac{{a + 5}}{{{a^2} - 25}} = \frac{{a + 5}}{{\left( {a + 5} \right)\left( {a - 5} \right)}} = a - 5\) الف
\(\frac{{a + 5}}{{{a^2} - 25}} = \frac{{a + 5}}{{\left( {a + 5} \right)\left( {a - 5} \right)}} = \frac{1}{{a - 5}}\) ب
عبارت (ب) به درستی ساده شده است.
7 اگر \(A = {a^2} - {b^2}\) و \(B = {a^2} + {b^2}\) و \(C = 2ab\) ، حاصل عبارت \(\frac{{{A^2} - {B^2}}}{{{C^2}}}\) را به دست آورید.
\(\begin{array}{l}\left\{ \begin{array}{l}A = {a^2} - {b^2}\\\\B = {a^2} + {b^2}\\\\C = 2ab\end{array} \right.\\\\ \Rightarrow \frac{{{A^2} - {B^2}}}{{{C^2}}} = \\\\\frac{{{{({a^2} - {b^2})}^2} - {{({a^2} + {b^2})}^2}}}{{{{(2ab)}^2}}} = \\\\\frac{{({a^4} - 2{a^2}{b^2} + {b^4}) - ({a^4} + 2{a^2}{b^2} + {b^4})}}{{4{a^2}{b^2}}} = \\\\\frac{{{a^4} - 2{a^2}{b^2} + {b^4} - {a^4} - 2{a^2}{b^2} - {b^4}}}{{4{a^2}{b^2}}} = \\\\\frac{{ - 2{a^2}{b^2} - 2{a^2}{b^2}}}{{4{a^2}{b^2}}} = \frac{{ - 4{a^2}{b^2}}}{{4{a^2}{b^2}}} = - 1\end{array}\)
8 کدام یک از تساوی های زیر، درست و کدام یک نادرست است؟ موارد نادرست را اصلاح کنید. (همهٔ عبارت های جبری تعریف شده فرض می شود.)
\(\frac{a}{b} - \frac{b}{a} = \frac{{a - b}}{{ab}}\) الف
\(\frac{{{x^{13}}}}{{{x^{20}}}} = {x^7}\) ب
\(\frac{a}{5} - \frac{{7 - b}}{5} = \frac{{a - 7 - b}}{5}\) ج
\(\frac{{a - b}}{{b - a}} = 1\) د
\(\frac{1}{{a - b}} = \frac{{ - 1}}{{a + b}}\) هـ
\(\frac{{{a^2} - {b^2}}}{{a - b}} = a + b\) و
\(\frac{{ca + cb}}{{c + cd}} = \frac{{a + b}}{d}\) ز
\(\frac{{\frac{a}{b}}}{{\frac{a}{c}}} = \frac{c}{b}\) ح
\(\frac{a}{b} - \frac{b}{a} = \frac{{a - b}}{{ab}}\) الف
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\frac{a}{b} - \frac{b}{a} = \frac{{{a^2} - {b^2}}}{{ab}}\)
\(\frac{{{x^{13}}}}{{{x^{20}}}} = {x^7}\) ب
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\frac{{{x^{13}}}}{{{x^{20}}}} = {x^{13 - 20}} = {x^{ - 7}}\)
البته تساوی زیر برای آن نیز برقرار است:
\(\frac{{{x^{13}}}}{{{x^{20}}}} = \frac{1}{{{x^7}}} = {x^{ - 7}}\)
\(\frac{a}{5} - \frac{{7 - b}}{5} = \frac{{a - 7 - b}}{5}\) ج
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\begin{array}{l}\frac{a}{5} - \frac{{7 - b}}{5} = \frac{{a - (7 - b)}}{5} = \\\\\frac{{a - 7 + b}}{5}\end{array}\)
\(\frac{{a - b}}{{b - a}} = 1\) د
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\frac{{a - b}}{{b - a}} = \frac{{a - b}}{{ - (a - b)}} = - 1\)
\(\frac{1}{{a - b}} = \frac{{ - 1}}{{a + b}}\) هـ
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\frac{1}{{a - b}} = \frac{1}{{ - (b - a)}} = \frac{{ - 1}}{{b - a}}\)
\(\frac{{{a^2} - {b^2}}}{{a - b}} = a + b\) و
درست می باشد؛ زیرا:
\(\frac{{{a^2} - {b^2}}}{{a - b}} = \frac{{(a - b)(a + b)}}{{a - b}} = a + b\)
\(\frac{{ca + cb}}{{c + cd}} = \frac{{a + b}}{d}\) ز
نادرست است؛ حالت درست آن به صورت زیر می باشد:
\(\frac{{ca + cb}}{{c + cd}} = \frac{{c(a + b)}}{{c(1 + d)}} = \frac{{a + b}}{{1 + d}}\)
\(\frac{{\frac{a}{b}}}{{\frac{a}{c}}} = \frac{c}{b}\) ح
درست می باشد؛ زیرا:
\(\frac{{\frac{a}{b}}}{{\frac{a}{c}}} = \frac{a}{b} \div \frac{a}{c} = \frac{a}{b} \times \frac{c}{a} = \frac{c}{b}\)
9 طول مستطیلی از دو برابر عرض آن یک واحد کمتر است. نسبت محیط به مساحت این مستطیل را به صورت یک کسر گویا (عبارت گویا) بنویسید.
عرض = x
طول = 2x-1
\(:P = 2(2x - 1 + x) = 6x - 2\) محیط
\(:S = (2x - 1)x = 2{x^2} - x\) مساحت
\(\frac{P}{S} = \frac{{6x - 2}}{{2{x^2} - x}}\)
10 حاصل عبارت های زیر را به دست آورید و نتیجه را ساده کنید.
\(\frac{{\frac{{a - {a^2}}}{{{a^2} - 1}}}}{{\frac{a}{{a + 1}} - a}}\) الف
\(\frac{{\frac{1}{{x - y}} - \frac{2}{{x + y}}}}{{\frac{{{x^2} - 9{y^2}}}{{{{(x - y)}^2}}}}}\) ب
\(\frac{{\frac{{a - {a^2}}}{{{a^2} - 1}}}}{{\frac{a}{{a + 1}} - a}} = \frac{{\frac{{ - a(a - 1)}}{{(a - 1)(a + 1)}}}}{{\frac{{a - a(a + 1)}}{{a + 1}}}} = \) الف
\(\begin{array}{l}\frac{{\frac{{ - a}}{{a + 1}}}}{{\frac{{a - {a^2} - a}}{{a + 1}}}} = \frac{{\frac{{ - a}}{{a + 1}}}}{{\frac{{ - {a^2}}}{{a + 1}}}} = \\\\\frac{{ - a}}{{a + 1}} \times \frac{{a + 1}}{{ - {a^2}}} = \frac{{ - 1}}{a}\end{array}\)
\(\frac{{\frac{1}{{x - y}} - \frac{2}{{x + y}}}}{{\frac{{{x^2} - 9{y^2}}}{{{{(x - y)}^2}}}}} = \) ب
\(\begin{array}{l}\frac{{\frac{{(x + y) - 2(x - y)}}{{(x - y)(x + y)}}}}{{\frac{{{x^2} - {{(3y)}^2}}}{{{{(x - y)}^2}}}}} = \\\\\frac{{\frac{{x + y - 2x + 2y}}{{(x - y)(x + y)}}}}{{\frac{{(x + 3y)(x - 3y)}}{{{{(x - y)}^2}}}}} = \\\\\frac{{\frac{{ - x + 3y}}{{(x - y)(x + y)}}}}{{\frac{{(x + 3y)(x - 3y)}}{{{{(x - y)}^2}}}}} = \\\\\frac{{\frac{{ - (x - 3y)}}{{(x - y)(x + y)}}}}{{\frac{{(x + 3y)(x - 3y)}}{{{{(x - y)}^2}}}}} = \\\\\frac{{ - (x - 3y)}}{{(x - y)(x + y)}} \times \frac{{{{(x - y)}^2}}}{{(x + 3y)(x - 3y)}} = \\\\\frac{{ - 1}}{{x + y}} \times \frac{{x - y}}{{x + 3y}} = \\\\\frac{{y - x}}{{{x^2} + 3xy + xy + 3{y^2}}} = \\\\\frac{{y - x}}{{{x^2} + 4xy + 3{y^2}}}\end{array}\)
11 دو عبارت گویا بنویسید که :
الف حاصل ضرب آنها \(\frac{{a - 2}}{{a + 7}}\) شود.
ب حاصل جمع آنها \(\frac{{a - 2}}{{a + 7}}\) شود.
الف
عبارت های دو تایی گویای زیادی می توان نوشت که حاصل ضرب آن ها برابر با \(\frac{{a - 2}}{{a + 7}}\) شود:
\(\begin{array}{l}\left\{ \begin{array}{l}1\\\\\frac{{a - 2}}{{a + 7}}\end{array} \right. \Rightarrow 1 \times \frac{{a - 2}}{{a + 7}} = \frac{{a - 2}}{{a + 7}}\,\\\\\left\{ \begin{array}{l}a - 2\\\\\frac{1}{{a + 7}}\end{array} \right. \Rightarrow (a - 2) \times \frac{1}{{a + 7}} = \frac{{a - 2}}{{a + 7}}\\\\\left\{ \begin{array}{l}\frac{{{a^2} - 4}}{{a + 3}}\\\\\frac{{a + 3}}{{{a^2} + 9a + 14}}\end{array} \right.\\\\ \Rightarrow \frac{{{a^2} - 4}}{{a + 3}} \times \frac{{a + 3}}{{{a^2} + 9a + 14}} = \\\\\frac{{(a - 2)(a + 2)}}{{a + 3}} \times \frac{{a + 3}}{{(a + 2)(a + 7)}} = \\\\\frac{{a - 2}}{{a + 7}}\end{array}\)
ب
عبارت های دو تایی گویای زیادی می توان نوشت که حاصل جمع آن ها برابر با \(\frac{{a - 2}}{{a + 7}}\) شود:
\(\begin{array}{l}\left\{ \begin{array}{l}\frac{a}{{a + 7}}\\\\\frac{{ - 2}}{{a + 7}}\end{array} \right. \Rightarrow \frac{a}{{a + 7}} + \frac{{ - 2}}{{a + 7}} = \frac{{a - 2}}{{a + 7}}\\\\\left\{ \begin{array}{l}\frac{{4a - 5}}{{a + 7}}\\\\\frac{{2 - 3a}}{{a + 7}}\end{array} \right. \Rightarrow \frac{{4a - 5}}{{a + 7}} + \frac{{2 - 3a}}{{a + 7}} = \frac{{a - 2}}{{a + 7}}\end{array}\)
12 عرض مستطیل مقابل را برحسب x به دست آورید. مساحت مستطیل \({x^2} - 9\) است.

\( = \frac{{{x^2} - x - 12}}{{x - 4}}\) طول
= طول ÷ مساحت مستطیل = عرض
\(\begin{array}{l}({x^2} - 9) \div \frac{{{x^2} - x - 12}}{{x - 4}} = \\\\(x - 3)(x + 3) \times \frac{{x - 4}}{{{x^2} - x - 12}} = \\\\(x - 3)(x + 3) \times \frac{{x - 4}}{{(x + 3)(x - 4)}} = \\\\(x - 3) \times \frac{{(x + 3)(x - 4)}}{{(x + 3)(x - 4)}} = x - 3\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















