1736019749.png)
جواب فعّالیت صفحه 116 درس 7 ریاضی نهم (عبارت های گویا)
تعداد بازدید : 78.78Mپاسخ فعّالیت صفحه 116 ریاضی نهم
-گام به گام فعّالیت صفحه 116 درس عبارت های گویا
-فعّالیت صفحه 116 درس 7
-شما در حال مشاهده جواب فعّالیت صفحه 116 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
هر یک از عبارت های گویای زیر چگونه ساده شده است؟ هر جا لازم است، راه حل را کامل کنید (چگونگی استفاده از اتحادها و تجزیه را در هر مورد توضیح دهید.)
\(\frac{{18{y^3}}}{{60{y^5}}} = \frac{3}{{10{y^2}}}\) الف
\(\frac{{{x^2} + 6x + 9}}{{{x^2} + 4x + 3}} = \frac{{\left( {x + 3} \right)\left( {x + 3} \right)}}{{\left( {x + 1} \right)\left( {x + 3} \right)}} = \frac{{x + 3}}{{x + 1}}\) ب
\(\frac{{{y^2} - 9}}{{3y + 9}} = \frac{{\left( {y + 3} \right)\left( {y - 3} \right)}}{{3\left( {y + 3} \right)}} = \_\_\_\_\_\_\_\_\_\_\_\_\) ج
\(\frac{{8a{b^7}}}{{20{a^2}{b^3}}} = \frac{{2{b^4}}}{{}}\) د
\(\frac{{b - 5}}{{5 - b}} = \frac{{b - 5}}{{ - \left( {b - 5} \right)}} = - 1\) هـ
\(\frac{{18{y^3}}}{{60{y^5}}} = \frac{3}{{10{y^2}}}\) الف
\( \Rightarrow \frac{{18{y^3}}}{{60{y^5}}} = \frac{{3y \times 6{y^2}}}{{10{y^3} \times 6{y^2}}} = \frac{3}{{10{y^2}}}\)
از ب.م.م صورت و مخرج استفاده شده؛ در این قسمت ب.م.م صورت مخرج برابر با \(6{y^2}\) می باشد.
\(\frac{{{x^2} + 6x + 9}}{{{x^2} + 4x + 3}} = \frac{{\left( {x + 3} \right)\left( {x + 3} \right)}}{{\left( {x + 1} \right)\left( {x + 3} \right)}} = \frac{{x + 3}}{{x + 1}}\) ب
از تجزیه صورت و مخرج استفاده شده و سپس عامل مشترک با هم ساده شده اند. عامل مشترک در این عبارت در صورت و مخرج پس از تجزیه، عبارت x+3 می باشد که خط می خورد.
\(\frac{{{y^2} - 9}}{{3y + 9}} = \frac{{\left( {y + 3} \right)\left( {y - 3} \right)}}{{3\left( {y + 3} \right)}} = \frac{{y - 3}}{3}\) ج
صورت را به کمک اتحاد مزدوج، تجزیه می کنیم؛ همچنین مخرج را با استفاده از فاکتورگیری یا همان ب.م.م که عدد 3 می باشد، تجزیه می کنیم؛ حال عامل مشترک صورت و مخرج را که عبارت y+3 می باشد را خط می زنیم و عبارت گویا را ساده می کنیم.
\(\frac{{8a{b^7}}}{{20{a^2}{b^3}}} = \frac{{2{b^4}}}{{}}\) د
\(\begin{array}{l} \Rightarrow \frac{{8a{b^7}}}{{20{a^2}{b^3}}} = \frac{{2{b^4} \times 4a{b^3}}}{{5a \times 4a{b^3}}} = \frac{{2{b^4}}}{{5a}}\\\\ \Rightarrow \frac{{8a{b^7}}}{{20{a^2}{b^3}}} = \frac{{2{b^4}}}{{5a}}\end{array}\)
ب.م.م دو عبارت صورت و مخرج را بدست می آوریم که برابر با \(4a{b^3}\) می شود؛ این عامل مشترک را در صورت و مخرج خط می زنیم.
\(\frac{{b - 5}}{{5 - b}} = \frac{{b - 5}}{{ - \left( {b - 5} \right)}} = - 1\) هـ
ب.م.م دو عبارت صورت و مخرج را بدست می آوریم که برابر با b-5 می باشد؛ این عامل مشترک را در صورت و مخرج خط می زنیم.
چطور عبارت های گویا را ساده کنیم؟
برای اینکه عبارت های گویا را ساده کنیم، بایستی ببینیم که این عبارت های گویا از چه عامل های درست شده اند. بیایید مثالی که همه ما با آن آشنا هستیم بزنیم. کسر زیر را در نظر بگیرید. می خواهیم آن را به ساده ترین حالت تبدیل کنیم:
\(\frac{{30,030}}{{3,675}} = \)
ابتدا بررسی می کنیم که اعداد صورت و کسر از ضرب چه اعدادی به وجود می آیند. ابتدا صورت کسر را بررسی می کنیم:
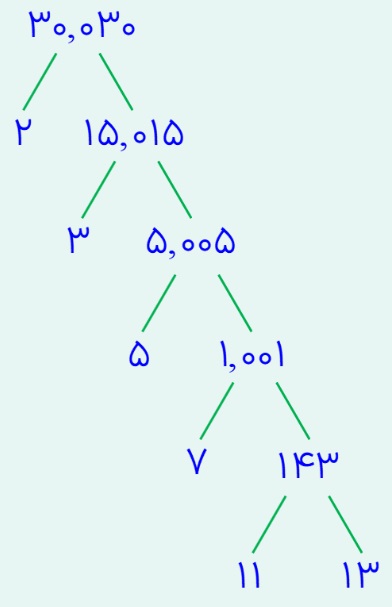
بنابراین عدد 30,030 به عامل های اول تبدیل می شود:
\(30,030 = 2 \times 3 \times 5 \times 7 \times 11 \times 13\)
حال به سراغ مخرج کسر می رویم:
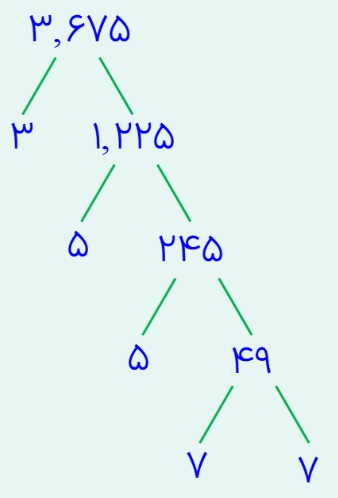
بنابراین عدد 3,675 به عامل های اول تبدیل می شود:
\(\left( {30,030\,\,\,,\,\,\,3,0675} \right) = 3 \times 5 \times 7 = 105\)
بنابراین داریم:
\(\begin{array}{l}\frac{{30,030}}{{3,675}} = \frac{{2 \times 3 \times 5 \times 7 \times 11 \times 13}}{{3 \times {5^2} \times {7^2}}} = \\\\\frac{{2 \times 11 \times 13 \times 105}}{{5 \times 7 \times 105}} = \end{array}\)
حال عامل مشترک که عدد 105 هست را حذف می کنیم:
\(\frac{{{x^2} + 2x + 1}}{{{x^2} - 1}} = \)
ابتدا صورت و مخرج را به صورت ضرب چند جمله ای تبدیل می کنیم. ابتدا به عبارت داخل صورت می پردازیم. می دانیم که عبارت \({x^2} + 2x + 1\) از اتحاد مربع دو جمله ای ها به صورت زیر می شود:
\({x^2} + 2x + 1 = {(x + 1)^2}\)
حال به عبارت داخل مخرج می پردازیم. می دانیم که به کمک اتحاد مزدوج به صورت زیر می شود:
\({x^2} - 1 = (x - 1)(x + 1)\)
عامل مشترک بین عبارت های صورت و مخرج، x+1 می باشد. با حذف این عبارت از صورت و مخرج، عبارت گویای مورد نظر ساده می شود:
\(\frac{{{x^2} + 2x + 1}}{{{x^2} - 1}} = \frac{{{{(x + 1)}^2}}}{{(x - 1)(x + 1)}} = \frac{{x + 1}}{{x - 1}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
