جواب فعالیت صفحه 20 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 78.79Mپاسخ فعالیت صفحه 20 ریاضی یازدهم تجربی
-گام به گام فعالیت صفحه 20 درس هندسۀ تحلیلی و جبر
-فعالیت صفحه 20 درس 1
-شما در حال مشاهده جواب فعالیت صفحه 20 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 معادلهٔ مقابل را حل کنید.
\(\frac{{2x}}{{{x^2} - 1}} + \frac{2}{{x + 1}} = \frac{{2 - x}}{{{x^2} - x}}\;\;\;\;\left( 1 \right)\)
الف ابتدا در صورتِ امکان مخرج کسرها را به حاصل ضرب عامل های اول تجزیه می کنیم:
\(\frac{{2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{2}{{\left( {x + 1} \right)}} = \frac{{2 - x}}{{}}\;\;\;\;\left( 2 \right)\)
ب در مخرج ها سه نوع عامل اولِ متمایز وجود دارد x، (x+1) و (…….) که بزرگ ترین توان هر کدام از آنها برابر ..... است؛ پس ک م م مخرج ها عبارت است از ................
پ طرفین معادلهٔ (2) را در x(x-1)(x+1) ضرب می کنیم تا معادله از شکل کسری خارج شود.
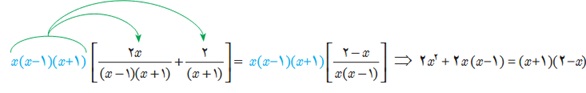
ت پس از ساده کردن، معادلهٔ \(5{x^2} - 3x - 2 = 0\) حاصل می شود.
ث برای معادلهٔ درجه دوم اخیر، مقدار ) را به دست آورید و معادله را حل کنید. آیا هر دو جواب به دست آمده مورد قبول اند؟ چرا؟
الف
\(\frac{{2x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{2}{{\left( {x + 1} \right)}} = \frac{{2 - x}}{{x\left( {x - 1} \right)}}\;\;\;\;\left( 2 \right)\)
ب
در مخرج ها سه نوع عامل اولِ متمایز وجود دارد x، (x+1) و (x-1) که بزرگ ترین توان هر کدام از آنها برابر 1 است؛ پس ک م م مخرج ها عبارت است از x(x-1)(x+1)
ث
\(5{x^2} - 3x - 2 = 0 \Rightarrow \Delta = {\left( { - 3} \right)^2} - 4\left( 5 \right)\left( { - 2} \right) = 49 \Rightarrow x = \frac{{3 \pm \sqrt {49} }}{{10}} \Rightarrow \left\{ \begin{array}{l}{x_1} = \frac{{3 + 7}}{{10}} = 1\\{x_2} = \frac{{3 - 7}}{{10}} = - 0/4\end{array} \right.\)
1← غ ق ق
4/0 ← ق ق
خیر؛ تنها یکی از جواب ها قابل قبول است، زیرا اگر 1 = x ، آنگاه مخرج کسر برابر صفر می شود و عبارت تعریف نشده خواهد بود .
2 خط یک متروی تهران به طول 60 کیلومتر، میدان تجریش را به فرودگاه بین المللی امام خمینی (قُدِّسَ سِرُّهُ) متصل می کند. برای انجام یک آزمایش، قطاری مسیر شمال به جنوب این خط را با سرعت ثابت v کیلومتر بر ساعت و بدون توقف در ایستگاه ها طی می کند. اگر در مسیر جنوب به شمال، از سرعت قطار 10 km/h کاسته شود، زمان بازگشت نیم ساعت طولانی تر از زمان رفت خواهد شد. مطلوب است محاسبهٔ طول زمان رفت و زمان برگشت این قطار.
الف توضیح دهید، چرا زمان رفت از رابطهٔ \(\frac{{60}}{v}\) به دست می آید؟
ب عبارتی بر حسب v بنویسید که زمان برگشت را نشان دهد.
پ توضیح دهید که چرا معادلهٔ \(\frac{{60}}{{v - 10}} = \frac{{60}}{v} + \frac{1}{2}\) برقرار است.
ت طرفین این معادله را در ک م م مخرج ها ضرب کنید تا به یک معادلهٔ درجه دوم تبدیل شود.
ث از حل معادلهٔ حاصل، سرعت قطار در مسیر رفت را بیابید و به کمک آن، زمان رفت و زمان برگشت قطار را به دست آورید.
الف می دانیم مسافت طی شده برابر است با حاصل ضرب سرعت متوسط در زمان، یعنی v.t=x . در نتیجه اگر زمان رفت را با t1 نمایش دهیم، داریم:
\(x = v.{t_1} \Rightarrow {t_1} = \frac{x}{v} \Rightarrow {t_1} = \frac{{60}}{v}\)
ب زمان برگشت را با t2 نمایش می دهیم و می دانیم که از سرعت قطار 10 km/hکاسته شده است؛ پس داریم :
\(60 = \left( {v - 10} \right) \times {t_2} \Rightarrow {t_2} = \frac{{60}}{{v - 10}}\)
پ با توجه به اینکه زمان بازگشت نیم ساعت طولانی تر بوده است، پس داریم :
\({t_2} = {t_1} + \frac{1}{2} \Rightarrow \frac{{60}}{{v - 10}} = \frac{{60}}{v} + \frac{1}{2}\)
ت ک م م مخرج ها 2v(v-10) است؛ بنابراین :
؟
ث سرعت رفت قطار در مسیر شمال به جنوب 40 km/hاست:
\({t_1} = \frac{{60}}{{40}} = \frac{3}{2}\) زمان رفت: ساعت
\({t_2} = \frac{{60}}{{40 - 10}} = 2\) زمان برگشت: ساعت
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















