جواب کاردرکلاس صفحه 7 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 84.72Mپاسخ کاردرکلاس صفحه 7 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 7 درس هندسۀ تحلیلی و جبر
-کاردرکلاس صفحه 7 درس 1
-شما در حال مشاهده جواب کاردرکلاس صفحه 7 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 مثلث با رأس های A(1,9) ، B(3,1) و C(7,11) را در نظر بگیرید و آن را در دستگاه مختصات مقابل مشخص کنید.

الف مختصات M، نقطهٔ وسط ضلع BC را مشخص کنید.
ب طول میانهٔ AM را محاسبه کنید.
پ معادلهٔ خطی که میانهٔ AM روی آن قرار دارد را به دست آورید.
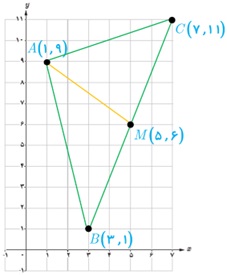
الف
\(M\left( {{x_M}\;,\;{y_M}} \right) \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{3 + 7}}{2} = 5\\{y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{1 + 11}}{2} = 6\end{array} \right. \Rightarrow M\left( {{x_M}\;,\;{y_M}} \right) = M\left( {5\;,\;6} \right)\)
ب
\(AM = \sqrt {{{\left( {{x_A} - {x_M}} \right)}^2} + {{\left( {{y_A} - {y_M}} \right)}^2}} = \sqrt {{{\left( {1 - 5} \right)}^2} + {{\left( {9 - 6} \right)}^2}} = \sqrt {16 + 9} = 5\)
پ
\(\begin{array}{l}{m_{AM}} = \frac{{{y_A} - {y_M}}}{{{x_A} - {x_M}}} = \frac{{9 - 6}}{{1 - 5}} = - \frac{3}{4}\\ \Rightarrow {L_{AM}}:\quad y = - \frac{3}{4}x + h\mathop \Rightarrow \limits^{M\left( {5\;,\;6} \right)} 6 = - \frac{3}{4} \times 5 + h \Rightarrow h = \frac{{39}}{4}\\ \Rightarrow y = - \frac{3}{4}x + \frac{{39}}{4}\end{array}\)
2
الف نقطۀ N(5,-4) وسط پاره خط واصل بین دو نقطهٔ A و B(7,-2) است. مختصات نقطۀ A را بیابید.
ب قرینهٔ نقطهٔ C(1,2) نسبت به نقطهٔ M(-1,4) را به دست آورید.
پ قرینهٔ نقطهٔ P(α,$) نسبت به مبدأ مختصات را به دست آورید.
الف
\(N\left( {5\;,\; - 4} \right) \Rightarrow \left\{ \begin{array}{l}5 = \frac{{{x_A} + 7}}{2} \Rightarrow {x_A} + 7 = 10 \Rightarrow {x_A} = 3\\ - 4 = \frac{{{y_A} + \left( { - 2} \right)}}{2} \Rightarrow {y_A} - 2 = - 8 \Rightarrow {y_A} = - 6\end{array} \right. \Rightarrow A\left( {{x_A}\;,\;{y_A}} \right) = A\left( {3\;,\; - 6} \right)\)
ب
\(M\left( { - 1\;,\;4} \right) \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_C} + {x_{C'}}}}{2} \Rightarrow - 1 = \frac{{1 + {x_{C'}}}}{2} \Rightarrow {x_{C'}} = - 3\\{y_M} = \frac{{{y_C} + {y_{C'}}}}{2} \Rightarrow 4 = \frac{{2 + {y_{C'}}}}{2} \Rightarrow {y_{C'}} = 6\end{array} \right. \Rightarrow C'\left( {{x_{C'}}\;,\;{y_{C'}}} \right) = C'\left( { - 3\;,\;6} \right)\)
پ
\(O\left( {0\;,\;0} \right) \Rightarrow \left\{ \begin{array}{l}{x_O} = \frac{{{x_P} + {x_{P'}}}}{2} = 0 \Rightarrow {x_P} + {x_{P'}} = 0 \Rightarrow {x_{P'}} = - {x_P}\\{y_O} = \frac{{{y_P} + {y_{P'}}}}{2} = 0 \Rightarrow {y_P} + {y_{P'}} = 0 \Rightarrow {y_{P'}} = - {y_P}\end{array} \right. \Rightarrow P'\left( {{x_{P'}}\;,\;{y_{P'}}} \right) = \left( { - {x_P}\;,\; - {y_P}} \right)\)
3 سود سالانهٔ یک کارگاه کوچک تولیدی از سال 1385 تا 1395 طبق نمودار مقابل سیر صعودی داشته است. به کمک رابطهٔ نقطهٔ وسط پاره خط، به سؤالات زیر پاسخ دهید:
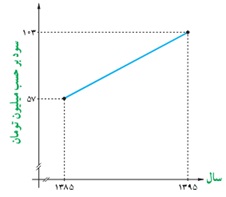
الف میانگین سود سالانهٔ این شرکت در دههٔ مورد نظر چقدر بوده است؟
ب در کدام سال، مقدار سود سالانه، با این میانگین سود ده ساله برابر بوده است؟
پ اگر سود سالانه در طول یک دههٔ آینده با همین روند افزایش یابد، انتظار می رود در سال 1405 سود سالانه شرکت چقدر باشد؟
الف
میانگین سود سالانه: \( = \frac{{103 + 57}}{2} = 80\)
ب
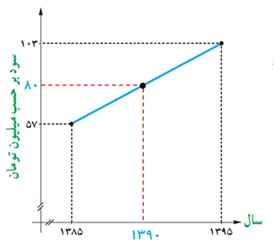
\( = \frac{{1385 + 1395}}{2} = 1390\)سال مورد نظر
پ
\(\begin{array}{l}m = \frac{{103 - 57}}{{1395 - 1385}} = \frac{{46}}{{10}} = 4/6\\ \Rightarrow y = 4/6x + h\quad \mathop \Rightarrow \limits^{\left( {1385\;,\;57} \right)} 57 = 4/6 \times 1385 + h \Rightarrow h = - 6314\\ \Rightarrow y = 4/6x - 6314 \Rightarrow x = 1405 \Rightarrow y = 4/6 \times 1405 - 6314 = 149\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















