شاه کلید نکات
شاه کلید سوال
1 دایرهٔ مقابل به مرکز O و به شعاع 2 سانتی متر داده شده است.
اندازه ضلع PQ در مثلث OPQ را با استفاده از نسبت های مثلثاتی سال گذشته به دست آورید.
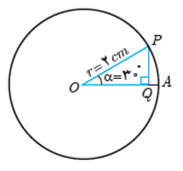
\(\begin{array}{l}\sin \alpha = \frac{{PQ}}{{OP}} \Rightarrow \sin {30^ \circ }\\\\ = \frac{1}{2} = \frac{{PQ}}{2} \Rightarrow PQ = 1\end{array}\)
2 باتوجه به اینکه کمان °30 برابر \(\frac{1}{{12}}\) کل محیط دایره است (چرا؟) می توان طول کمان روبه رو به زاویه α (یعنی کمان PA) را به صورت زیر به دست آورد.
\() = \frac{1}{{12}} \times 2\pi \times 2 = \) محیط دایره\(\mathop {PA}\limits^\frown {\mkern 1mu} = \frac{1}{{12}} \times (\)
\(\frac{4}{{12}}\pi = \frac{\pi }{3}\,cm\)
چرا که کل دایره 360 درجه است و :
\(\frac{1}{{12}} \times {360^ \circ } = {30^ \circ }\)
اکنون به مرکز O دایره های دیگری به شعاع های 1 و 3 سانتی متر رسم می کنیم (شکل روبه رو).
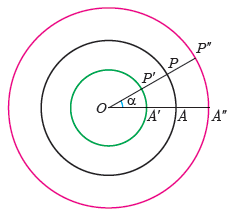
الف مطابق فرمول بالا طول کمان های \(\mathop {P'A'}\limits^\frown \) و \(\mathop {P''A''}\limits^\frown \) را که روبه رو به زاویه \(\alpha= {30^\circ }\) هستند به دست آورید.
\(\begin{array}{l}\mathop {P'A'}\limits^\frown {\mkern 1mu} = ..........\\\\\mathop {P''A''}\limits^\frown {\mkern 1mu} = ..........\end{array}\)
ب در هر دایره نسبت طول کمان روبه رو به زاویه α به شعاع آن دایره را محاسبه کنید. این نسبت ها با هم چه رابطه ای دارند؟
\(\begin{array}{l}\frac{{\mathop {PA}\limits^\frown }}{{OP}} = ......\\\\\frac{{\mathop {P'A'}\limits^\frown }}{{OP'}} = ......\\\\\frac{{\mathop {P''A''}\limits^\frown }}{{OP''}} = ......\end{array}\)
پ اگر در شکل صفحهٔ قبل دایره ای به شعاع r و به مرکز O در نظر بگیریم، آیا نسبت فوق در آن دایره تغییری می کند؟ چرا؟ با تکمیل رابطه زیر، به این سؤال پاسخ دهید.
\(\frac{{\frac{1}{{12}} \times 2\pi \times r}}{r} = ...........\)
ت در سؤال قبل دیدیم که نسبت طول کمان روبه رو به زاویه °30 به شعاع، در همه دایره ها برابر مقدار ثابت .............. است. اکنون در سؤال زیر به این می پردازیم که این نسبت چه زمانی برابر 1 است.
الف
\(\begin{array}{l}\mathop {P'A'}\limits^\frown {\mkern 1mu} = \frac{1}{{12}} \times 2\pi \, \times 1 = \frac{\pi }{6}\;cm\\\\\mathop {P''A''}\limits^\frown {\mkern 1mu} = \frac{1}{{12}} \times 2\pi \, \times 3 = \frac{\pi }{2}\;cm\end{array}\)
ب
\(\begin{array}{l}\frac{{\mathop {PA}\limits^\frown }}{{OP}} = \frac{{\frac{\pi }{3}}}{2} = \frac{\pi }{6}\\\\\frac{{\mathop {P'A'}\limits^\frown }}{{OP'}} = \frac{{\frac{\pi }{6}}}{1} = \frac{\pi }{6}\\\\\frac{{\mathop {P''A''}\limits^\frown }}{{OP''}} = \frac{{\frac{\pi }{2}}}{3} = \frac{\pi }{6}\end{array}\)
پ
زیرا شعاع r از صورت و مخرج ناپدید می شود.
\(\frac{{\frac{1}{{12}} \times 2\pi \times r}}{r} = \frac{\pi }{6}\)
ت
\(\frac{\pi }{6}\)
3 در یک دایره به شعاع r، مانند شکل زیر، طول کمان روبه رو به زاویهٔ \(\theta \) (کمان L) برابر طول شعاع دایره است. نسبت طول کمان به شعاع چقدر است؟
اندازهٔ زاویهٔ q تقریباً چند درجه است؟ (از نقاله استفاده کنید).
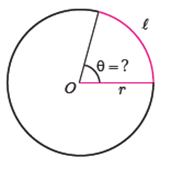
\(\begin{array}{l}\frac{l}{r} = 1\\\theta \simeq 57/{3^ \circ }\end{array}\)
1736019749.png)
