جواب تمرین صفحه 39 درس 2 هندسه دوازدهم (آشنایی با مقاطع مخروطی)
تعداد بازدید : 84.73Mپاسخ تمرین صفحه 39 هندسه دوازدهم
-گام به گام تمرین صفحه 39 درس آشنایی با مقاطع مخروطی
-تمرین صفحه 39 درس 2
-شما در حال مشاهده جواب تمرین صفحه 39 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 مکان هندسی هر یک از مجموعه نقاط زیر را مشخص کنید:
الف نقاطی از صفحه که از دو خط متقاطع \(d\) و \(d'\) به یک فاصله اند.
ب مرکزهای همه دایره هایی در صفحه که بر خط \(d\) در نقطه ثابت \(A\) مماس اند.
پ مرکزهای همه دایره هایی با شعاع ثابت \(r\) که بر خط \(d\) در صفحه مماس اند.
ت مرکزهای همه دایره هایی با شعاع ثابت \(r\) که بر دایره \(C(O,r)\) در صفحه این دایره مماس خارجی اند.
الف مکان هندسی نقطه ای از صفحه اکه از دو خط متقاطع \(d\) و \(d'\) به یک فاصله است. دو خط عمود بر هم می باشد که هر یک از آن ها نیمساز زاویه ی دو خط \(d\) و \(d'\) است.

ب مکان هندسی مرکز دایره ای که در نقطه \(A\) بر خط \(d\) مماس است. خطی که در نقطه \(A\) بر \(d\) عمود می باشد.
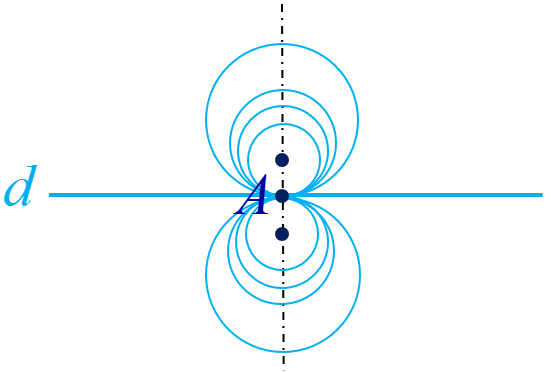
پ مکان هندسی مرکز دایره ای به شعاع \(r\) که در صفحه بر خط \(d\) مماس است، دو خط موازی با خط \(d\) می باشد که فاصله هر یک از آن ها از \(d\) مساوی \(r\) است.

ت مکان هندسی مرکز دایره ای به شعاع \(r\) که بر دایره ی \(C(O,r)\) مماس خارج است، دایره ی \(C(O,2r)\) می باشد.

2 نقاط \(A\)، \(B\)، \(C\) و \(D\) در صفحه مفروض اند. نقطه ای در این صفحه بیابید که از \(A\) و \(B\) به یک فاصله و از \(C\) و \(D\) نیز به یک فاصله باشد (بحث کنید.)
کافی است محل تقاطع عمودمنصف های دو پاره خط \(CD\) و \(AB\) را تعیین کنیم.
بحث: اگر \(AB||CD\) عمودمنصف های این دو پاره خط، یکدیگر را فقط در یک لحظه قطع می کنند و مسأله در این حالت فقط یک جواب دارد.
ولی اگر \(AB||CD\) عمود منصف های این دو پاره خط، موازی اند و مسأله در این حالت فقط هیچ جوابی جواب ندارد.
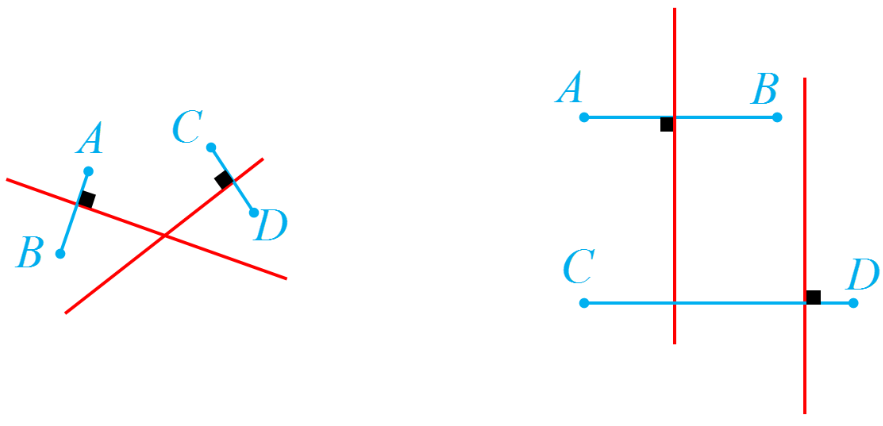
3 نقاط \(A\)، \(B\) و \(C\) در صفحه مفروض اند. نقطه ای بیابید که از \(A\) و \(B\) به یک فاصله و از \(C\) به فاصله 3 سانتیمتر باشد (بحث کنید.)
کافی است محل تقاطع عمود منصف پاره خط \(AB\) و دایره ای به مرکز \(C\) و شعاع را 3 تعیین کنیم.
بحث:
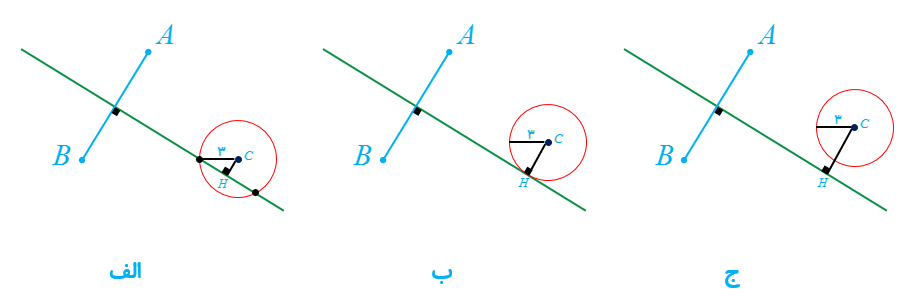
فرض کنیم \(d\) عمودمنصف پاره خط \(AB\) است؛ اگر \(CH\) فاصله \(C\) تا خط \(d\) باشد، سه حالت زیر را به تفکیک بررسی می کنیم.
الف اگر \(CH<3\) ، در این حالت خط \(d\) دایره را در 2 نقطه قطع می کند و مسأله دو جواب دارد.
ب اگر \(CH=3\) ، در این حالت خط \(d\) بر دتیره مماس و دایره را در 1 نقطه قطع می کند؛ لذا مسأله فقط یک جواب دارد.
ج اگر \(CH>3\) ، در این حالت خط \(d\) ، دایره را قطع نمی کند و مسأله هیچ جوابی ندارد.
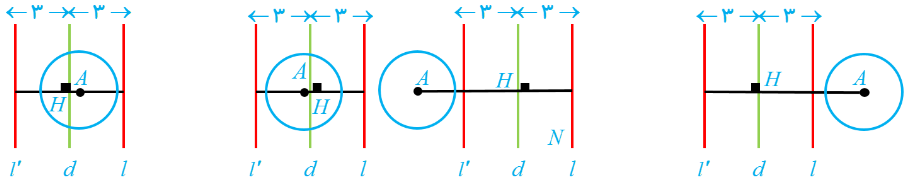
4 نقطه \(A\) و خط \(d\) در صفحه مفروض اند. نقطه ای بیابید که از \(A\) به فاصله 2 سانتیمتر و از \(d\) به فاصله 3 سانتیمتر باشد (بحث کنید.)
مکان هندسی نقطه ای که از \(A\) به فاصله 2 باشد، دایره ای به مرکز \(A\) و شعاع 2 است و مکان هندسی نقطه ای که از خط \(d\) به فاصله 3 باشد، دو خط \(l\) و \(l'\) موازی با خط \(d\) است که فاصله هر یک از آن ها از \(d\) مساوی 3 است. محل تقاطع این دو مکان هندسی پاسخ مسأله می باشد.
بحث:
فرض کنیم \(AH\) فاصله \(A\) تا خط \(d\) باشد. با توجه به اندازه شعاع دایره و مکان نقطه \(A\) یکی از حالت های زیر رخ می دهد:
الف اگر \(1 ، (\(3-2=1\) ، \(3+2=5\)) خط \(l\) (یا خط \(l'\)) دایره را در دونقطه قطع می کند و مسأله دارای دو جواب است:
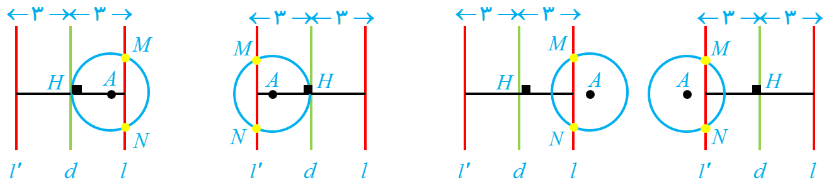
ب اگر \(AH=5\) یا \(AH=1\) ، خط \(l\) (یا خط \(l'\)) دایره را در یک نقطه قطع می کند و مسأله دارای یک جواب است:
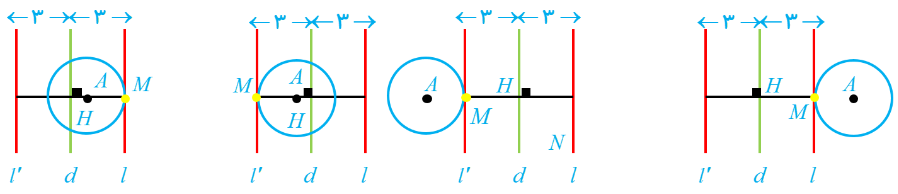
پ اگر \(AH>5\) یا \(AH<1\) ، خط \(l\) (یا خط \(l'\)) دایره را در هیچ نقطه ای قطع نمی کند و مسأله جوابی ندارد:
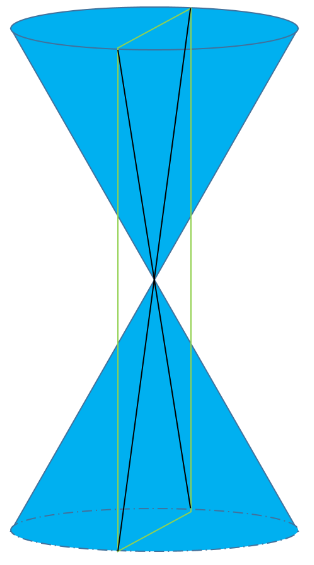
5 هرگاه صفحه ای شامل محور یک سطح مخروطی، آن را برش دهد، فصل مشترک (مقطع) حاصل چه شکل است؟
مکان هندسی خواسته شده دو خط متقاطع می باشد.
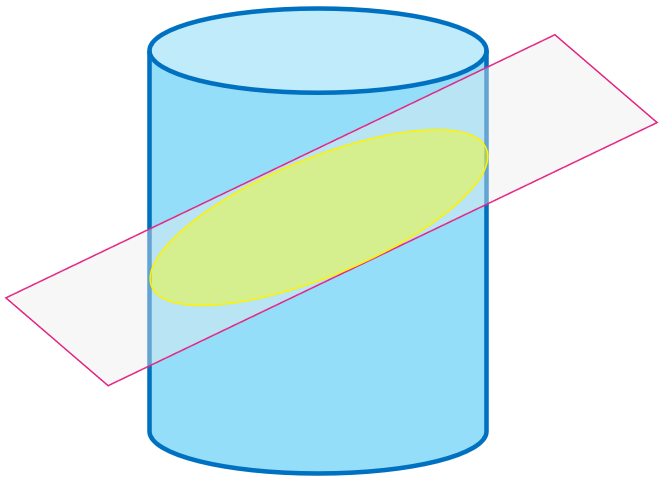
6 هرگاه دو خط \(d\) و \(l\) موازی باشند، از دوران \(d\) حول \(l\) سطحی ایجاد می شود که آن را یک سطح استوانه ای می نامیم. حال فرض کنید صفحه \(P\)، یک سطح استوانه ای را قطع کند. در حالت های مختلف درباره سطح مقطع حاصل بحث کنید (چهار حالت).
الف اگر خط \(l\) با صفحه \(P\) موازی بوده و فاصله دو خط \(l\) و \(d\) بیشتر از فاصله خط \(l\) تا صفحه \(P\) باشد، سطح مقطع ایجاد شده سطح بین دو خط موازی است.
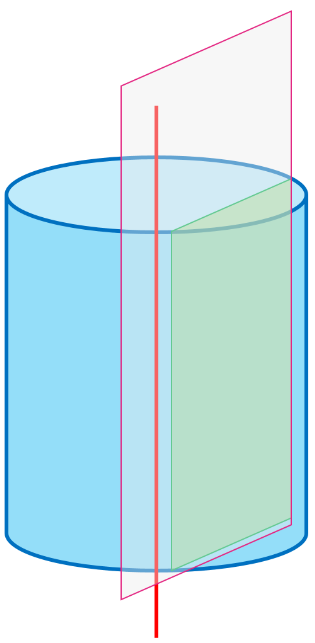
ب اگر خط \(l\) با صفحه \(P\) موازی بوده و فاصله دو خط \(l\) و \(d\) مساوی با فاصله خط \(l\) تا صفحه \(P\) باشد، سطح مقطع ایجاد شده فقط یک خط موازی با \(l\) است.

ج اگر خط \(l\) بر صفحه \(P\) عمود باشد، سطح مقطع ایجاد شده سطح یک دایره است.

د اگر خط \(l\) بر صفحه \(P\) عمود متقاطع بوده ولی بر هم عمود نباشند، سطح مقطع ایجاد شده سطح یک بیضی است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















