آیا تمام سوالات فعالیت 6 صفحه 52 هندسه دوازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعالیت 6 صفحه 52 هندسه دوازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعالیت 6 صفحه 52 درس 2 هندسه دوازدهم (آشنایی با مقاطع مخروطی)

تعداد بازدید : 78.8M

پاسخ فعالیت 6 صفحه 52 هندسه دوازدهم

گام به گام فعالیت 6 صفحه 52 درس آشنایی با مقاطع مخروطی

فعالیت 6 صفحه 52 درس 2

شما در حال مشاهده جواب فعالیت 6 صفحه 52 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

١ فرض کنید نقطه F(a, 0) که در آن a مثبت است، کانون سهمی و خط هادی d موازی محور yها به معادله x=-a باشد و نقطه P(x, y) نقطه ای دلخواه واقع بر سهمی باشد. داریم: |PF|=|PB| چرا؟

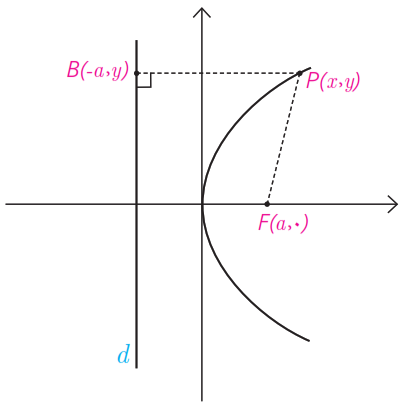
به این دلیل که نقطه P بر روی سهمی قرار دارد.

\(\begin{array}{l}PF = PH\\\\ \Rightarrow \sqrt {{{(x + a)}^2} + {{(y - 0)}^2}} = \sqrt {{{(x - a)}^2} + {{(y - y)}^2}} \\\\ \Rightarrow {y^2} = - 4ax\end{array}\)

بنابراین

\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{\left( {x + a} \right)}^2} + {{\left( {y - y} \right)}^2}}\)

با به توان ٢ رساندن دو طرف و ساده کردن عبارات خواهیم داشت: \({y^2} = 4ax\)

دقت کنید که a برابر با فاصله کانون تا رأس سهمی و همچنین فاصله رأس سهمی تا خط هادی است و فاصله کانون تا خط هادی برابر 2a است. در این حالت عدد مثبت a را فاصله کانونی سهمی می نامند و چنان که دیده می شود خطی که از کانون به خط هادی سهمی عمود می شود که در اینجا محور xهاست محور تقارن سهمی است که به آن محور کانونی سهمی یا محور سهمی هم می گوییم.

٢ در حالتی که خط هادی d موازی محور yها به معادله x=a باشد ولی کانون F(-a,0) در سمت چپ آن قرار داشته باشد با انجام مراحل قسمت (1) نشان دهید که در این حالت معادله سهمی به صورت \({y^2} = - 4ax\) است. در این حالت محور xها محور سهمی است.

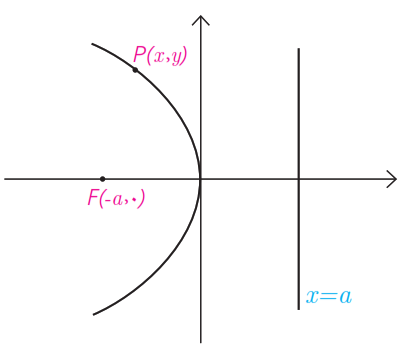
\(\begin{array}{l}PF = PH\\\\ \Rightarrow \sqrt {{{(x - 0)}^2} + {{(y - a)}^2}} = \sqrt {{{(x - x)}^2} + {{(y + a)}^2}} \\\\ \Rightarrow {x^2} = 4ay\end{array}\)

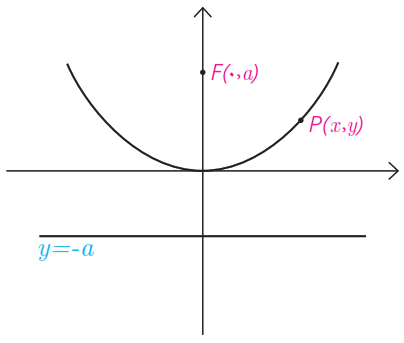
٣ در حالتی که خط هادی d موازی محور xها به معادله y=-a و کانون F(0,a) در بالای آن قرار دارد با انجام مراحل قسمت (1) نشان دهید که در این حالت معادله سهمی به صورت \({x^2} = 4ay\) است. در این حالت محور yها محور سهمی است.

(در واقع این معادله همان \(y = \frac{1}{{4a}}{x^2}\) است که در پایه دهم به عنوان معادله سهمی با آن آشنا شدید)

٤ در حالتی که خط هادی d موازی محور xها به معادله y=a و کانون F(0,-a) در زیر آن قرار دارد با انجام مراحل قسمت (1) نشان دهید در این حالت معادله سهمی به صورت \({x^2} = - 4ay\) است. در این حالت محور yها محور سهمی است.

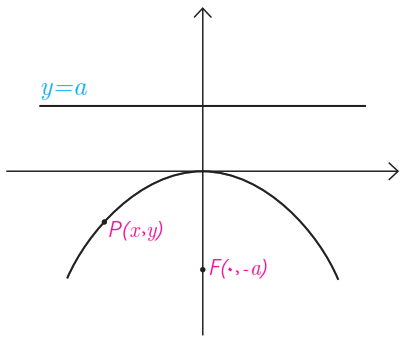
\(\begin{array}{l}PF = PH\\\\ \Rightarrow \sqrt {{{(x - 0)}^2} + {{(y + a)}^2}} = \sqrt {{{(x - x)}^2} + {{(y - a)}^2}} \\\\ \Rightarrow {x^2} = - 4ay\end{array}\)