1736019749.png)
جواب فعالیت 1 صفحه 47 درس 2 هندسه دوازدهم (آشنایی با مقاطع مخروطی)
تعداد بازدید : 78.8Mپاسخ فعالیت 1 صفحه 47 هندسه دوازدهم
-گام به گام فعالیت 1 صفحه 47 درس آشنایی با مقاطع مخروطی
-فعالیت 1 صفحه 47 درس 2
-شما در حال مشاهده جواب فعالیت 1 صفحه 47 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
یک تکه نخ درنظر گرفته و دوسر آن را مطابق شکل در دو نقطه F و F’ ثابت کنید. فرض کنید طول نخ l باشد و ′l > FF یک قلم را مانند شکل داخل نخ کنید و منحنی ای به گونه ای رسم کنید که در تمام زمان رسم، دوطرف نخ به صورت صاف و کشیده شده باشد. شکل حاصل منحنی بسته ای خواهد بود که بیضی نام دارد.
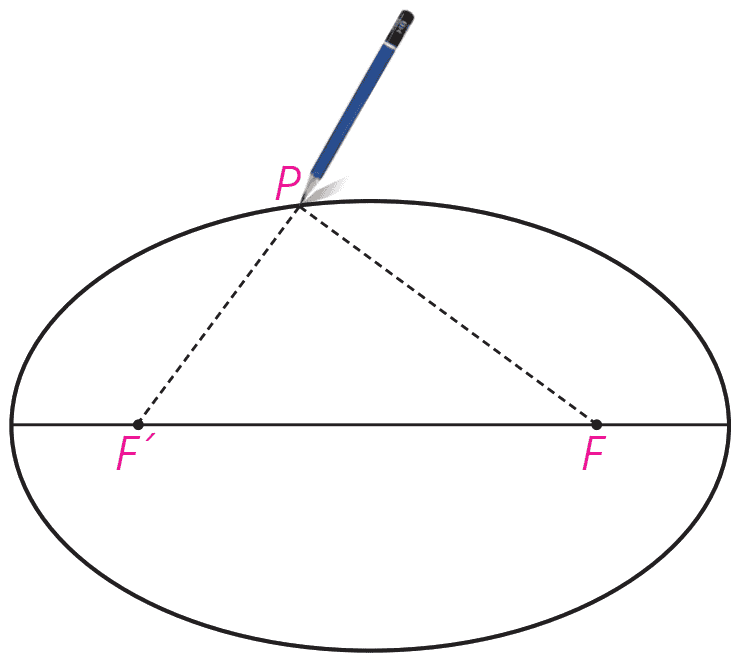
1 یک نقطه دلخواه روی شکل رسم شده درنظر بگیرید. مجموع فاصله های این نقطه از دو نقطه ثابت F و ′F برابر چیست؟
\(PF + PF' = l\)
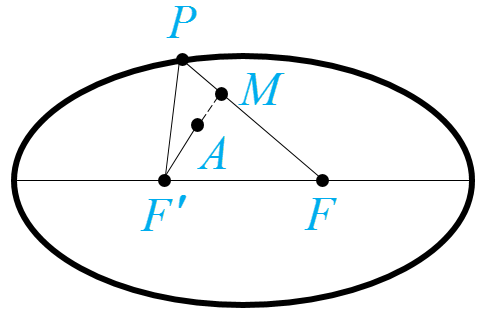
2 یک نقطه دلخواه مانند A در درونِ بیضی رسم شده درنظر بگیرید و آن را به دو نقطه ثابت F و ′F وصل کنید و نشان دهید مجموع فواصل نقطه موردنظر از F و ′F کوچکتر از l است.
(راهنمایی: پاره خط FA را از سمت A امتداد دهید تا بیضی را قطع کند. سپس از نامساوی مثلثی استفاده نمایید)
فرض کنیم r نقطه ای درون بیضی باشد که روی خط FF' قرار نداشته باشد. نقطه P را روی بیضی چنان اختیار می کنیم که A دورن مثلث PFF' باشد. اگر امتداد AF' ، ضلع PF را در نقطه M قطع کند، در این صورت بنا به قضیه نامساوی مثلث داریم:
\(\begin{array}{l}\Delta PF'M:F'M < PF' + PM\\\\\Delta AFM:AF < AM + MF\\\\ \Rightarrow AF + F'M < PF' + PM + AM + MF\\\\ \Rightarrow AF + F'A + AM < PF' + PM + AM + MF\\\\ \Rightarrow AF + AF' < PF' + PF\\\\ \Rightarrow AF + AF' < l\end{array}\)
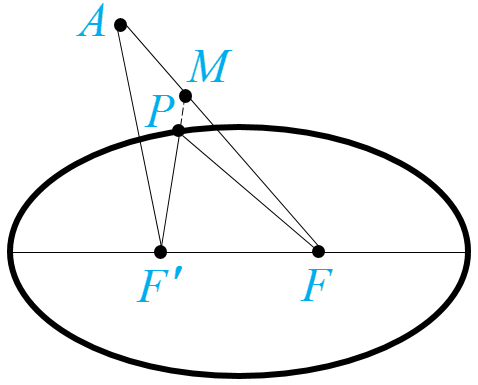
3 یک نقطه دلخواه مانند B بیرون بیضی رسم شده درنظر بگیرید و آن را به دو نقطه F و ′F وصل کنید و نشان دهید مجموع فواصل نقطه موردنظر از F و ′F بزرگتر از l است.
(راهنمایی: اگر نقطه D محل برخورد FB با بیضی باشد، F′D را رسم کنید و از نامساوی مثلثی استفاده نمایید).
فرض کنیم A نقطه ای بیرون بیضی باشد که روی خط FF' قرار نداشته باشد. نقطه P را روی بیضی چنان اختیار می کنیم که A دورن مثلث AFF' باشد. اگر امتداد PF' ، ضلع AF را در نقطه M قطع کند، در این صورت بنا به قضیه نامساوی مثلث داریم:
\(\begin{array}{l}\Delta AF'M:F'M < AF' + AM\\\\\Delta PFM:PF < PM + MF\\\\ \Rightarrow PF + F'M < AF' + AM + PM + MF\\\\ \Rightarrow PF + F'P + PM < AF' + AM + PM + MF\\\\ \Rightarrow PF + F'P < AF' + AF\\\\ \Rightarrow l < AF + AF'\end{array}\)
4 از مراحل (1) تا (3) متوجه وجود چه ویژگی مشترکی در همه نقاط بیضی شدید که هیچ نقطه دیگری از صفحه، آن ویژگی را ندارد؟
ویژگی تمام نقاط بیضی این است که مجموع فواصل آن ها از دو نقطه ثابت، مقداری ثابت است.
5 با توجه به آنچه گفته شد تعریف بیضی را که با استفاده از مکان هندسی در زیر آمده است تکمیل نمایید.
بیضی مکان هندسی نقاطی از صفحه است که مجموع فواصلشان از دو ..................... یک مقدار ..................... است.
بیضی مکان هندسی نقاطی از صفحه است که مجموع فواصلشان از دو ...نقطه ثابت... یک مقدار ...ثابت... است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
