جواب تمرین صفحه 46 درس 2 هندسه دوازدهم (آشنایی با مقاطع مخروطی)

الف

\(\begin{array}{l}r = OA = \sqrt {{{(3 - 1)}^2} + {{(2 - 1)}^2}} = \sqrt 5 \\\\ \Rightarrow {(x - 1)^2} + {(y - 1)^2} = 5\end{array}\)

ب

\(\begin{array}{l}r = OH = \frac{{\left| {3(2) + 4(1)} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2\\\\ \Rightarrow {(x - 2)^2} + {(y - 1)^2} = 4\end{array}\)

پ

\(\begin{array}{l}AB = 2 \Rightarrow AH = BJ = 1\\\\OH = \frac{{\left| {1( - 1) + 1( - 1)} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{3}{{\sqrt 2 }}\\\\r = \sqrt {A{H^2} + B{H^2}} = \\\\\sqrt {1 + \frac{9}{2}} = \sqrt {\frac{{11}}{2}} \\\\ \Rightarrow {(x + 1)^2} + {(y + 1)^2} = \frac{{11}}{2}\end{array}\)

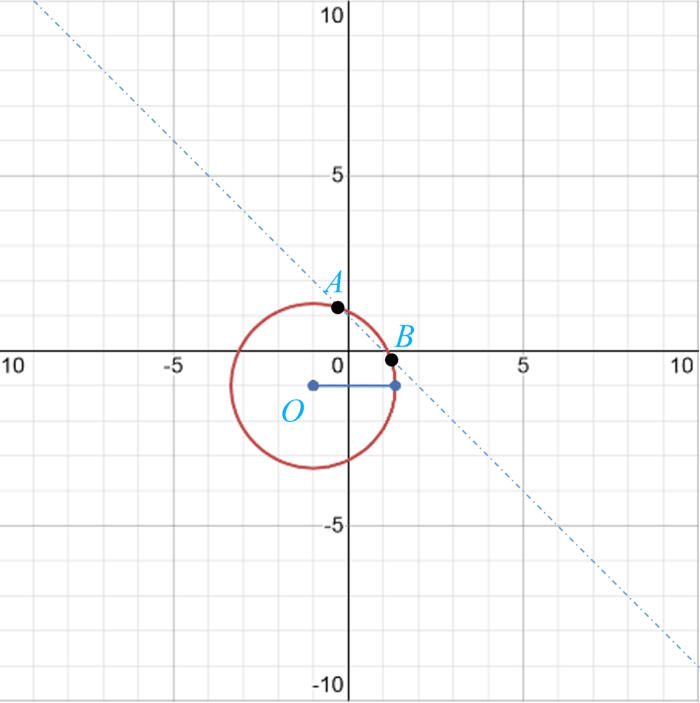
ت

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 1\\\\x - y = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 2\\\\y = - 1\end{array} \right.\\\\ \Rightarrow O'(2\;,\; - 1)\\\\r = \frac{{\left| {4(2) + 3( - 1) - 6} \right|}}{{\sqrt {16 + 9} }} = \frac{1}{5}\\\\ \Rightarrow {(x - 2)^2} + {(y + 1)^2} = \frac{1}{{25}}\end{array}\)

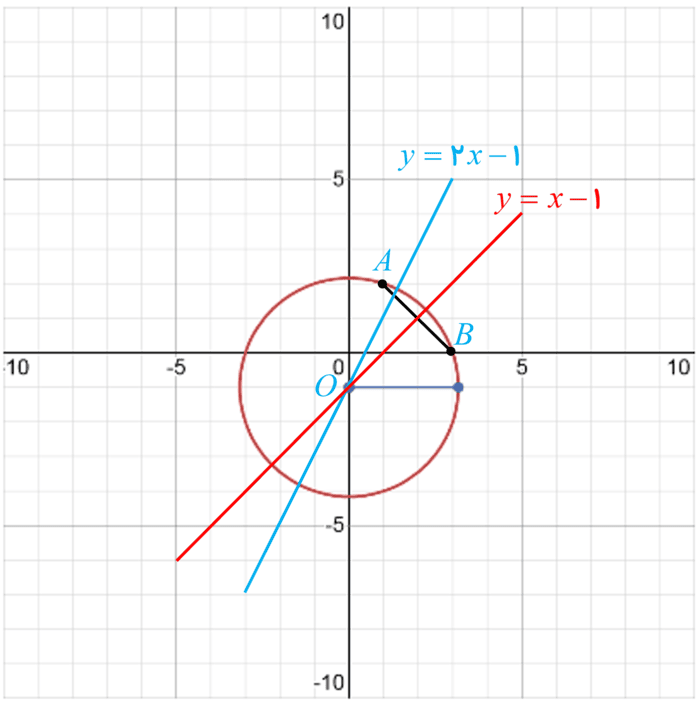
ث

\(\begin{array}{l}A(1\;,\;2)\;,\;B(3\;,\;0)\\\\ \Rightarrow M(\frac{{1 + 3}}{2},\frac{{2 + 0}}{2}) = (2\;,\;1)\\\\{m_{AB}} = \frac{{0 - 2}}{{3 - 1}} = - 1\\\\ \Rightarrow m' = \frac{{ - 1}}{m} = \frac{{ - 1}}{{ - 1}} = 1\\\\ \Rightarrow y - 1 = 1(x - 2)\\\\ \Rightarrow y = x - 1\\\\\left\{ \begin{array}{l}y = x - 1\\\\y = 2x - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 0\\\\y = - 1\end{array} \right.\\\\ \Rightarrow O'(0\;,\;1)\\\\ \Rightarrow r = O'A = \\\\\sqrt {{{(1 - 0)}^2} + {{( - 1 - 2)}^2}} = \sqrt {10} \\\\ \Rightarrow {x^2} + {(y + 1)^2} = 10\end{array}\)

\(\begin{array}{l}{x^2} + {y^2} - 3x + 5y + a = 0\\\\ \Rightarrow {A^2} + {B^2} - 4C = \\\\9 + 25 - 4a > 0\\\\ \Rightarrow 34 - 4a > 0\\\\ \Rightarrow a < \frac{{34}}{4} = \frac{{17}}{2}\end{array}\)

\(\begin{array}{*{20}{l}}{{x^2} + {y^2} - 2x + 4y - 5 = 0}\\{}\\{A( - 1\:, - 1)}\\{}\\\begin{array}{l} \Rightarrow {( - 1)^2} + {( - 1)^2} - 2( - 1) + 4( - 1) - 5\\\\ = - 5 < 0\end{array}\end{array}\)

نقطه درون دایره قرار دارد

\(\begin{array}{l}B(1\;,\, - 2)\\\\ \Rightarrow {1^2} + {( - 2)^2} - 2(1) + 4( - 2) - 5 = - 10 < 0\end{array}\)

نقطه درون دایره قرار دارد

\(\begin{array}{l}C(2\;,\,3)\\\\ \Rightarrow {(2)^2} + {(3)^2} - 2(2) + 4(3) - 5 = 16 > 0\end{array}\)

نقطه بیرون دایره قرار دارد

\(\begin{array}{l}D(4\;,\, - 1)\\\\ \Rightarrow {(4)^2} + {( - 1)^2} - 2(4) + 4( - 1) - 5 = 0\end{array}\)

نقطه روی دایره قرار دارد

الف

\(\begin{array}{l}{x^2} + {y^2} = 4\\\\ \Rightarrow O(0\;,\;0)\;,\;r = 2\\\\{x^2} + {y^2} - 2x = 4\\\\ \Rightarrow \left\{ \begin{array}{l}O'(1\;,\;0)\\\\r' = \sqrt 5 \end{array} \right.\\\\d = \sqrt {{{(1 - 0)}^2} + {{(0 - 0)}^2}} = 1\;,\;\\\\r + r' = 2 + \sqrt 5 \\\\\left| {r - r'} \right| = \sqrt 5 - 2\\\\ \Rightarrow \left| {r - r'} \right| < d < r + r'\end{array}\)

دو دایره متقاطع هستند.

ب

\(\begin{array}{l}{x^2} + {(y - 1)^2} = 1\\\\ \Rightarrow \left\{ \begin{array}{l}O(0\;,\;1)\\\\r = 1\end{array} \right.\\\\{(x - 1)^2} + {y^2} = 1\\\\ \Rightarrow \left\{ \begin{array}{l}O'(1\;,\;0)\\\\r' = 1\end{array} \right.\\\\d = \sqrt {{{(1 - 0)}^2} + {{(0 - 1)}^2}} = \sqrt 2 \\\\r + r' = 2\\\\\left| {r - r'} \right| = 0\\\\ \Rightarrow \left| {r - r'} \right| < d < r + r'\end{array}\)

دو دایره متقاطع هستند.

ج

\(\begin{array}{l}{x^2} + {y^2} = 1\\\\ \Rightarrow \left\{ \begin{array}{l}O(0\;,\;0)\\\\r = 1\end{array} \right.\\\\{x^2} + {y^2} - 3\sqrt 2 x - 3\sqrt 2 y + 5 = 0\\\\ \Rightarrow \\\left\{ \begin{array}{l}O'(\frac{{3\sqrt 2 }}{2}\;,\;\frac{{3\sqrt 2 }}{2})\\\\r' = \frac{{\sqrt {18 + 18 - 4(5)} }}{2} = 2\end{array} \right.\\\\d = \sqrt {{{(\frac{{3\sqrt 2 }}{2} - 0)}^2} + {{(\frac{{3\sqrt 2 }}{2} - 0)}^2}} = 3\\\\r + r' = 3\\\\\left| {r - r'} \right| = 1 \Rightarrow d = r + r'\end{array}\)

دو دایره مماس برون هستند.

د

\(\begin{array}{l}{x^2} + {y^2} = 1\\\\ \Rightarrow \left\{ \begin{array}{l}O(0\;,\;0)\\\\r = 1\end{array} \right.\\\\{x^2} + {y^2} - 6x - 2y + 9 = 0\\\\ \Rightarrow \left\{ \begin{array}{l}O'(3\;,\;1)\\\\r' = 1\end{array} \right.\\\\d = OO' = \sqrt {{{(3 - 0)}^2} + {{(1 - 0)}^2}} = \sqrt {10} \\\\r + r' = 2\\\\\left| {r - r'} \right| = 0\\\\ \Rightarrow d > r + r'\end{array}\)

دو دایره متخارج هستند.

\(\begin{array}{l}A( - 1\;,\, - 1)\;,\,B(1\;,\,1)\\\\ \Rightarrow N(\frac{{1 + ( - 1)}}{2}\;,\,\frac{{1 + ( - 1)}}{2})\\\\ \Rightarrow N(0\;,\,0)\\\\{m_{AB}} = \frac{{1 - ( - 1)}}{{1 - ( - 1)}} = 1\\\\\mathop \Rightarrow \limits^{d \bot AB} \;\;{m_d} = - \frac{1}{{{m_{AB}}}} = - \frac{1}{1} = - 1\\\\ \Rightarrow y - 0 = ( - 1)(x - 0)\\\\ \Rightarrow y = - x\\\\C(1\;,\, - 3)\;,\,A( - 1\;,\, - 1)\\\\ \Rightarrow M(\frac{{1 + ( - 1)}}{2}\;,\,\frac{{( - 3) + ( - 1)}}{2})\\\\ \Rightarrow M(0\;,\, - 2)\\\\{m_{AC}} = \frac{{( - 3) - ( - 1)}}{{1 - ( - 1)}} = - 1\\\\\mathop \Rightarrow \limits^{d \bot AC} \;\;{m_d}^\prime = - \frac{1}{{{m_{AC}}}} = - \frac{1}{{ - 1}} = 1\\\\ \Rightarrow y - 0 = ( - 1)(x - 0)\\\\ \Rightarrow y - ( - 2) = 1(x - 0)\\\\ \Rightarrow y = x - 2\\\\ \Rightarrow \left\{ \begin{array}{l}y = - x\\\\y = x - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 1\\\\y = - 1\end{array} \right.\\\\ \Rightarrow O(1\;,\, - 1)\\\\ \Rightarrow r = OA = \\\\\sqrt {{{(1 + 1)}^2} + {{(1 - 1)}^2}} = 2\\\\ \Rightarrow {(x - 1)^2} + {(y + 1)^2} = 4\end{array}\)

الف

\(\begin{array}{l}{x^2} + {y^2} - 4x - 4y + 7 = 0\\\\ \Rightarrow \left\{ \begin{array}{l}O(2\;,\;2)\\\\r = \frac{{\sqrt {16 + 16 - 28} }}{2} = 1\end{array} \right.\\\\3x + 4y = 0\\\\ \Rightarrow OH = \frac{{\left| {3(2) + 4(2)} \right|}}{{\sqrt {9 + 16} }} = \frac{{14}}{5}\\\\ \Rightarrow OH > r\end{array}\)

خط، دایره را قطع نمی کند.

ب

\(\begin{array}{l}{x^2} + {y^2} = 2\\\\ \Rightarrow \left\{ \begin{array}{l}O(0\;,\;0)\\\\r = \sqrt 2 \end{array} \right.\\\\x + y = 2\\\\ \Rightarrow OH = \frac{{\left| {0 + 0 - 2} \right|}}{{\sqrt {1 + 1} }} = \sqrt 2 \\\\ \Rightarrow OH = r\end{array}\)

خط، بر دایره مماس است.

ج

\(\begin{array}{l}{x^2} + {y^2} - 2x - 2y - 2 = 0\\\\ \Rightarrow \left\{ \begin{array}{l}O(1\;,\;1)\\\\r = \frac{{\sqrt {4 + 4 + 8} }}{2} = 2\end{array} \right.\\\\x + y = 1\\\\ \Rightarrow OH = \frac{{\left| {1(1) + 1(1) - 1} \right|}}{{\sqrt {1 + 1} }} = \frac{{\sqrt 2 }}{2}\\\\ \Rightarrow OH < r\end{array}\)

خط، دایره را در دو نقطه قطع می کند.