جواب تمرین صفحه 142 درس 6 ریاضی دوازدهم تجربی (هندسه)
تعداد بازدید : 86.5Mپاسخ تمرین صفحه 142 ریاضی دوازدهم تجربی
-گام به گام تمرین صفحه 142 درس هندسه
-تمرین صفحه 142 درس 6
-شما در حال مشاهده جواب تمرین صفحه 142 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در هر دایره مختصات مرکز دایره و اندازهٔ شعاع آن را پیدا کنید، محل تقاطع هر دایره را با محورهای مختصات، در صورت وجود مشخص کنید و درستی پاسخ خود را به کمک رسم دایره بررسی کنید.
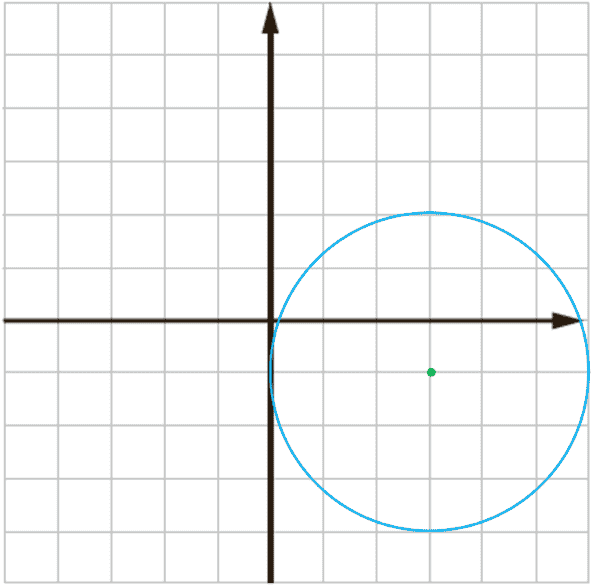
الف \({x^2} + {y^2} - 6x + 2y + 1 = 0\)
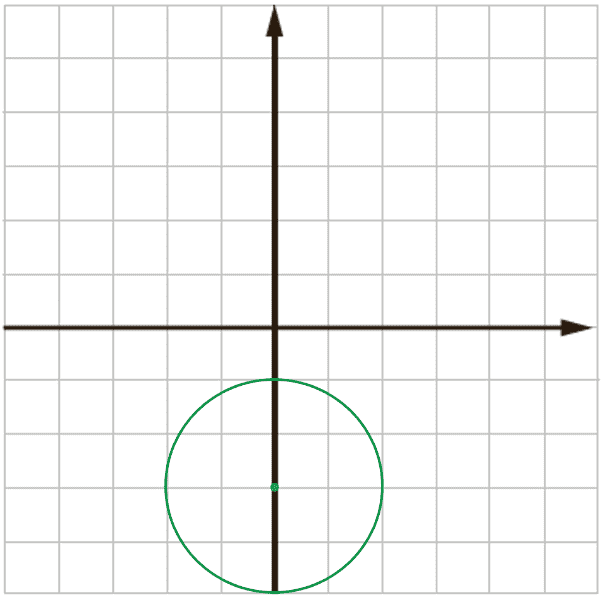
ب \({x^2} + {\left( {y + 3} \right)^2} - 4 = 0\)
الف
\(\begin{array}{l}O\left| \begin{array}{l}3\\ - 1\end{array} \right.\;\;\;\;\;\;\;\;r = \frac{1}{2}\sqrt {36 + 4 - 4} = 3\\\\x = 0 \Rightarrow {y^2} + 2y + 1 = 0\\\\ \Rightarrow y = - 1 \Rightarrow A\left| \begin{array}{l}0\\ - 1\end{array} \right.\end{array}\)
بر محور y مماس است :
\(y = 0 \Rightarrow {x^2} - 6x + 1 = 0 \Rightarrow x = 3 \pm 2\sqrt 2 > 0\)
دایره در سمت راست مبدأ محور x ها را قطع می کند:
ب
\(\begin{array}{l}O'\left| \begin{array}{l}0\\ - 3\end{array} \right.\;\;\;\;\;\;\;\;r' = 2\\\\x = 0 \Rightarrow {(y + 3)^2} = 4\\\\ \Rightarrow y = - 1\;,\;y = - 5\end{array}\)
دایره محور y ها را قطع می کند:
\(y = 0 \Rightarrow {x^2} + 9 - 4 = 0 \Rightarrow {x^2} = - 5\)
محور x ها را قطع نمی کند:
2 در حالت های زیر معادلهٔ دایره را بنویسید:
الف دایره ای که از مبدأ مختصات بگذرد و مرکز آن C(2,-1) باشد.
ب دایره ای که مرکز آن (2,3) و نقطۀ (-3,-9) نقطه ای روی آن باشد.
پ دایره ای که نقاط (0,3) و (-4,-1) دو سر یکی از قطرهای آن باشند.
الف
\(\begin{array}{l}OC = \sqrt {4 + 1} = \sqrt 5 = r\\\\{(x - 2)^2} + {(y + 1)^2} = 5\end{array}\)
ب
\(\begin{array}{l}CA = \sqrt {{{(2 + 3)}^2} + {{(3 + 9)}^2}} = \sqrt {169} = 13 = r\\\\{(x - 2)^2} + {(y - 3)^2} = 169\end{array}\)
پ وسط دو نقطه:
\(\begin{array}{l}C = (\frac{{0 + ( - 4)}}{2} = 2\;,\;\frac{{ - 1 + 3}}{2} = 1) = (2\;,\;1)\\\\2r = \sqrt {{{( - 4 - 0)}^2} + {{( - 1 - 3)}^2}} = 4\sqrt 2 \Rightarrow r = 2\sqrt 2 \\\\{(x + 2)^2} + {(y - 1)^2} = 8\end{array}\)
3 وضعیت نقاط (1,0) ، (0,-1) ، (-1,-2) و (0,0) را نسبت به دایرۀ \({x^2} + {y^2} - 2x + 4y + 1 = 0\) مشخص کنید.
\({x^2} + {y^2} - 2x + 4y + 1 = 0\)
روی دایره: \(P(1\;,\;0) = 1 + 0 - 2 + 0 + 1 = 0\)
خارج دایره: \(P(0\;,\;0) = 1 > 0\)
روی دایره: \(P( - 1\;,\; - 2) = 1 + 4 + 2 - 4 + 1 = 0\)
خارج دایره: \(P(2\;,\;3) = 4 + 9 - 6 + 2 + 10 > 0\)
4 شهرداری قصد دارد در یک فضای سبز دایره ای شکل به شعاع 1300 متر، دو مسیر پیاده روی مطابق شکل بسازد. اگر مختصات مرکز دایره (13,13) و هر واحد برابر 100 متر باشد:
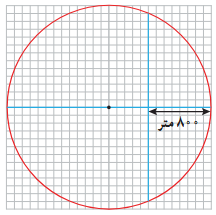
الف معادلهٔ این دایره چیست؟
ب مختصات نقاط برخورد دو مسیر را با دایره پیدا کنید.
پ دو مسیر در چه نقطه ای با یکدیگر متقاطع اند؟
ت طول مسیر عمودی چقدر است؟
الف
\(\begin{array}{l}{(x - 13)^2} + {(y - 13)^2} = 169\\\\x = 18 \Rightarrow 25 + {(y - 13)^2} = 169\\\\ \Rightarrow {(y - 13)^2} = 144\\\\ \Rightarrow \left\{ \begin{array}{l}y - 13 = 12 \Rightarrow y = 25\\\\y - 13 = - 12 \Rightarrow y = 1\end{array} \right.\end{array}\)
ب
\(A\left| \begin{array}{l}18\\1\end{array} \right.\;\;\;\;\;\;B\left| \begin{array}{l}18\\25\end{array} \right.\)
پ در نقطه \((5\;,\;0)\) یکدیگر را قطع می کنند.
ت
\(AB = 25 - 1 = 24 \Rightarrow 2400\) متر
5 معادلهٔ گستردهٔ یک دایره به شکل \({x^2} + {y^2} + 2x + 2y - 8 = 0\) است. مختصات مرکز دایره و اندازهٔ شعاع آن را پیدا کنید و معادلهٔ آن را به شکل استاندارد بنویسید.
\(\begin{array}{l}O\left| \begin{array}{l} - 1\\ - 1\end{array} \right.\;\;\;\;\\\\r = \frac{1}{2}\sqrt {4 + 4 + 32} = \sqrt {10} \;\;\;\;\;\;\;\;\\\\{(x + 1)^2} + {(y + 1)^2} = 10\end{array}\)
٦ وضع خط های زیر را نسبت به دایره مشخص کنید.
الف \(6x + 4y = 0\;\;,\;\;{x^2} + {y^2} - 4x - 4y + 7 = 0\)
ب \(y = - x - 2\;\;,\;\;{x^2} + {y^2} = 2\)
الف
\(\begin{array}{l}O\left| \begin{array}{l}2\\2\end{array} \right.\;\;\;\;r = \frac{1}{2}\sqrt {16 + 16 - 28} = 1\\\\d = \frac{{\left| {6(2) + 4(2)} \right|}}{{\sqrt {36 + 16} }} = \frac{{20}}{{\sqrt {52} }} = \frac{{10\sqrt {13} }}{{13}}\end{array}\)
خط و دایره نقطه مشترک ندارند؛ غیر متقاطع اند: \(d = \frac{{10\sqrt {13} }}{{13}} > r = 1\)
ب
\(\begin{array}{l}O\left| \begin{array}{l}0\\0\end{array} \right.\;\;\;\;r = \sqrt 2 \\\\x + y + 2 = 0\\\\d = \frac{{\left| {0 + 0 + 2} \right|}}{{\sqrt {1 + 1} }} = \sqrt 2 \end{array}\)
خط بر دایره مماس است: پ\(d = r = \sqrt 2 \)
7 اگر بدانیم خط l در نقطه (3,4) بر دایره ای به مرکز مبدأ مختصات مماس است، معادلهٔ خط مماس چیست؟
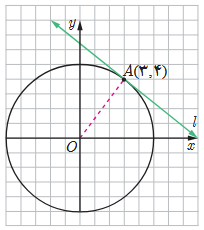
\(\begin{array}{l}OA = \sqrt {{3^2} + {4^2}} = 5 = r\\\\{x^2} + {y^2} = 25\\\\{m_{OA}} = \frac{{4 - 0}}{{3 - 0}} = \frac{4}{3} \Rightarrow m' = - \frac{3}{4}\;\;\;\;\;\;A\left| \begin{array}{l}3\\4\end{array} \right.\\\\y - 4 = - \frac{3}{4}(x - 3) \Rightarrow 3x + 4y - 25 = 0\end{array}\)
8 معادلهٔ دایره ای را بنویسید که مرکز آن، نقطهٔ (0,3) و بر خط 3x-4y=3 مماس باشد.
\(\begin{array}{l}d = \frac{{\left| {3(0) - 4(3) - 3} \right|}}{{\sqrt {{3^2} + {{( - 4)}^2}} }} = \frac{{15}}{5} = 3 = r\\\\{(x - 0)^2} + {(y - 3)^2} = 9 \Rightarrow {x^2} + {(y - 3)^2} = 9\end{array}\)
9 مشخص کنید در حالت های زیر دو دایره نسبت به هم چه وضعی دارند؟
الف \({x^2} + {y^2} - 2x + 4y = 4\;\;,\;\;{x^2} + {y^2} + 2x - 4y = 9\)
ب \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 7\;\;,\;\;{x^2} + {\left( {y - 5} \right)^2} = 5\)
الف
\(\begin{array}{l}O\left| \begin{array}{l}1\\ - 2\end{array} \right.\;\;\;\;r = \frac{1}{2}\sqrt {4 + 16 + 16} = 3\\\\O'\left| \begin{array}{l} - 1\\2\end{array} \right.\;\;\;\;r' = \frac{1}{2}\sqrt {4 + 16 + 36} = \sqrt {14} \\\\OO' = \sqrt {{{(1 + 1)}^2} + {{( - 2 - 2)}^2}} = 2\sqrt 5 \\\\ \Rightarrow r - r' < OO' < r + r' \to \end{array}\)
متقاطع اند
ب
\(\begin{array}{l}O\left| \begin{array}{l}2\\ - 3\end{array} \right.\;\;\;\;r = \sqrt 7 \\\\O'\left| \begin{array}{l}0\\5\end{array} \right.\;\;\;\;r' = \sqrt 5 \\\\OO' = \sqrt {{{(2 - 0)}^2} + {{( - 3 - 5)}^2}} = 2\sqrt {17} \\\\ \Rightarrow OO' > r + r' \to \end{array}\)
متخارجند
10 معادلهٔ دایره ای را بنویسید که مرکز آن (-1,-1) و با دایرۀ \({x^2} + {y^2} - 4x - 6y = 3\) مماس درون باشد.
\(\begin{array}{l}({x^2} - 4x + 4) + ({y^2} - 6y + 9) = 3 + 4 + 9\\\\ \Rightarrow {(x - 2)^2} + {(y - 3)^2} = {4^2}\\\\O\left| \begin{array}{l}2\\3\end{array} \right.\;\;\;r = 4\\\\O'\left| \begin{array}{l} - 1\\ - 1\end{array} \right.\;\;\;\\\\d = \sqrt {{{(2 + 1)}^2} + {{(3 + 1)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\\\\d = \left| {r - r'} \right| \Rightarrow 5 = \left| {r - 4} \right|\\\\ \Rightarrow \left\{ \begin{array}{l}r - 4 = 5 \Rightarrow r = 9\\\\r - 4 = - 5 \Rightarrow r = - 1\; \otimes \end{array} \right.\\\\ \Rightarrow {(x + 1)^2} + {(y + 1)^2} = 81\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















