1736019749.png)
جواب فعالیت صفحه 129 درس 6 ریاضی دوازدهم تجربی (هندسه)
تعداد بازدید : 78.8Mپاسخ فعالیت صفحه 129 ریاضی دوازدهم تجربی
-گام به گام فعالیت صفحه 129 درس هندسه
-فعالیت صفحه 129 درس 6
-شما در حال مشاهده جواب فعالیت صفحه 129 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
بیضی مقابل را در نظر بگیرید. اندازهٔ پاره خط های OA، OB و OF را به ترتیب با a، b و c نمایش داده ایم. می دانیم که مجموع فواصل هر نقطه از بیضی، از دو کانون بیضی مقداری ثابت است.
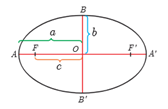
1 می خواهیم نشان دهیم قطر بزرگ بیضی طولی برابر با همین مقدار ثابت دارد. در رسم بیضی، حالتی را در نظر بگیرید که نوک مداد روی نقطهٔ A قرار دارد. در این صورت:
مقدار ثابت = AF + AF' = AF + (AF + FF') = 2AF + FF' (1)
الف) به همین ترتیب فرض کنید نوک مداد روی نقطهٔ A' قرار دارد. در این صورت داریم:
مقدار ثابت = A'F' + A'F = ………………….. (2)
ب) از مقایسهٔ رابطهٔ (1) و (2) و برابری سمت چپ دو رابطه داریم: AF = ……
پس:
مقدار ثابت = AF + AF' = ….. + AF' = ……
بنابراین:
مجموع فواصل هر نقطه از بیضی، از دو کانون آن، مقدار ثابتی است که برابر است با طول قطر بزرگ بیضی.
سؤال: با توجه به تساوی AF=A'F' نشان دهید که مرکز بیضی قطر بزرگ آن را نصف می کند و از آن نتیجه بگیرید طول قطر بزرگ بیضی برابر 2a است.
الف
مقدار ثابت \( = {\rm{ }}A'F'{\rm{ }} + {\rm{ }}A'F{\rm{ }} = {\rm{ }}A'F' + (A'F' + FF') = 2A'F' + FF'\) (2)
ب
\(AF = A'F'{\rm{ }}\)
مقدار ثابت \( = {\rm{ }}AF{\rm{ }} + {\rm{ }}AF'{\rm{ }} = {\rm{ }}A'F'{\rm{ }} + {\rm{ }}AF'{\rm{ }} = {\rm{ }}2a\)
\(\left. \begin{array}{l}AF = OA - OF \Rightarrow OF = OA - AF\\\\A'F' = OA' - OF' \Rightarrow OF' = OA' - AF'\end{array} \right\}\)
FF' نقطه میانی پاره خط \(O\;\; \Rightarrow \;\;OA - AF = OA' - A'F'\)
بنابر فرض
{AF = A'F'}
\( \Rightarrow OA = OA' = a \Rightarrow AA' = OA + OA' = a + a = 2a\)
2 حال قصد داریم رابطهٔ بین a، b و c را پیدا کنیم.
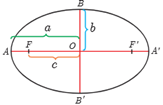
الف نقطۀ B را مطابق شکل روی بیضی در نظر بگیرید. می دانیم این نقطه روی عمود منصف پاره خط FF' است. (چرا؟)
ب به کمک قسمت قبلی فعالیت، اندازهٔ BF را پیدا کنید.
پ چه رابطه ای بین a، b و c وجود دارد؟
ت آیا مرکز بیضی قطر کوچک را هم نصف می کند؟ چرا؟
الف وسطFF’ است از طرفی BB’ بر AA’ عمود است؛ پس نتیجه می گیریم که OB عمود منصف FF’ است.
ب هر نقطه روی عمودمنصف از دو سر پاره خط به یک فاصله است.
\(\left. \begin{array}{l}BF = BF'\\BF + BF' = 2a\end{array} \right\} \to BF = BF' = a\)
پ
\(B\mathop O\limits^\Delta F:\quad B{F^2} = O{B^2} + O{F^2} \Rightarrow {a^2} = {b^2} + {c^2}\)
ت بله؛ می توان قسمت های الف و ب را برای قطر کوچک تحقیق کرد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
