شاه کلید نکات
شاه کلید سوال
1 با انجام مراحل زیر، معادلهٔ دایره ای را بنویسید که بر دایرهٔ \({x^2} + {y^2} + 2x - 4y - 4 = 0\) مماس بیرون و مرکز آن نقطهٔ O(2,-2) باشد:
- مختصات نقطهٔ O'، مرکز دایرهٔ داده شده عبارت است از: ....................................
- اندازۀ r' یعنی شعاع دایره داده شده برابر است با: ...........................................
- طول OO' برابر است با: ...........................................................
- شرط اینکه دو دایره مماس بیرونی باشند این است که: .................. پس شعاع r باید برابر ....... باشد.
- معادلهٔ دایرهٔ مطلوب را با معلوم بودن اندازهٔ شعاع و مختصات مرکز آن بنویسید: ........................................
- مختصات نقطهٔ O'، مرکز دایرهٔ داده شده عبارت است از: ...\(O'( - 1\;,\;2)\)...
- اندازۀ r' یعنی شعاع دایره داده شده برابر است با: ...\(r' = \frac{1}{2}\sqrt {4 + 16 + 16} = 3\)...
- طول OO' برابر است با: ...\(OO' = \sqrt {{{(2 + 1)}^2} + {{( - 2 - 2)}^2}} = 5\)...
- شرط اینکه دو دایره مماس بیرونی باشند این است که: ...\(5 = r + 3\)... پس شعاع r باید برابر ...2... باشد.
- معادلهٔ دایرهٔ مطلوب را با معلوم بودن اندازهٔ شعاع و مختصات مرکز آن بنویسید: ...\({(x - 2)^2} + {(y + 2)^2} = 4\)....
2 برای حالت های زیر معادلهٔ دو دایره را بنویسید و پاسخ خود را با دوستانتان مقایسه کنید.
الف دو دایره هم مرکز باشند.
ب دو دایره بیرون هم باشند.
الف
\(\left\{ \begin{array}{l}{(x - \alpha )^2} + {(y - \beta )^2} = {R^2}\\\\{(x - \alpha )^2} + {(y - \beta )^2} = {{R'}^2}\end{array} \right. \Rightarrow OO' = 0\)
ب
\(\left\{ \begin{array}{l}{(x - 3)^2} + {(y - 4)^2} = 4\\\\{x^2} + {y^2} = 1\end{array} \right.\)
3 برای موارد زیر وضعیت دو دایره را نسبت به هم مشخص کنید:
الف \({x^2} + {y^2} + 2x - 4y = 0\;\;,\;\;{x^2} + {y^2} - 2x + 4y = 0\)
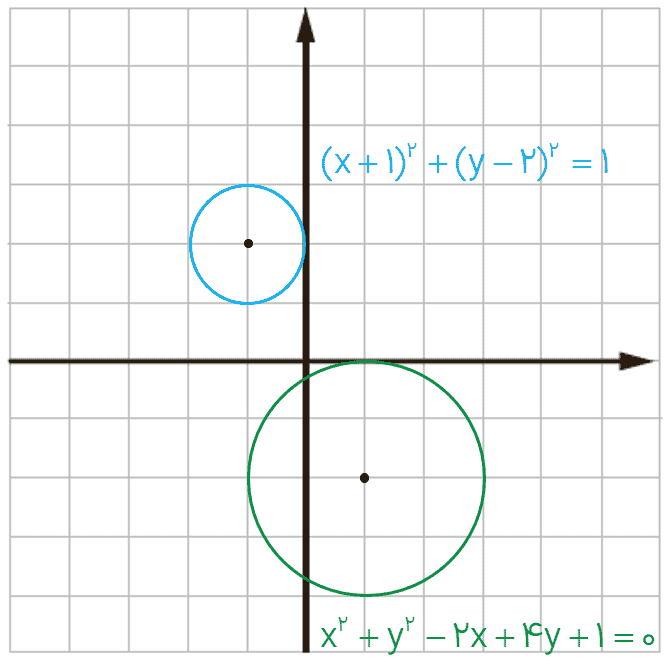
ب \({x^2} + {y^2} - 2x + 4y + 1 = 0\;\;,\;\;{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 1\)
الف
\(\begin{array}{l}O\left| \begin{array}{l}1\\ - 2\end{array} \right.\;\;\;\;\;\;\;\;r = \frac{1}{2}\sqrt {4 + 16} = \sqrt 5 \\\\O'\left| \begin{array}{l} - 1\\2\end{array} \right.\;\;\;\;\;\;\;\;r = \frac{1}{2}\sqrt {4 + 16} = \sqrt 5 \end{array}\)
\(OO' = \sqrt {{{(1 + 1)}^2} + {{( - 2 - 2)}^2}} = 2\sqrt 5 \Rightarrow OO' = r + r' \to \)
دو دایره مماس خارجند
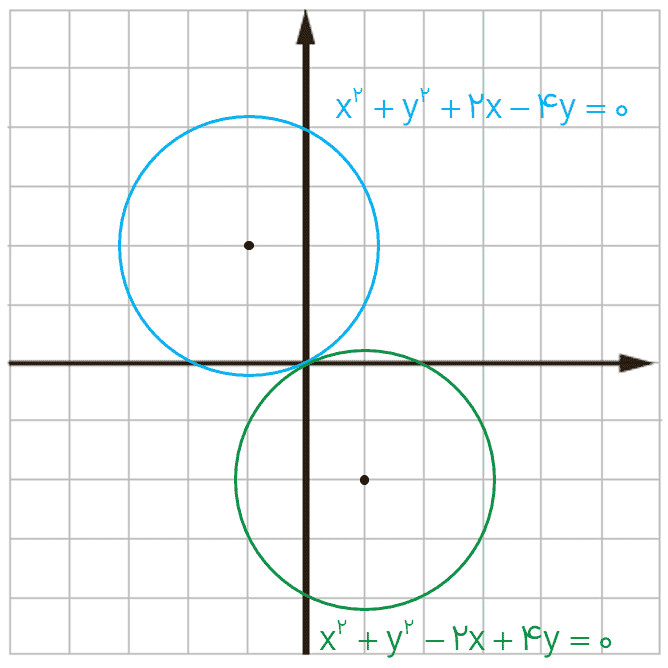
ب
\(\begin{array}{l}O\left| \begin{array}{l}1\\ - 2\end{array} \right.\;\;\;\;\;\;\;\;r = \frac{1}{2}\sqrt {4 + 16 - 4} = 2\\\\O'\left| \begin{array}{l} - 1\\2\end{array} \right.\;\;\;\;\;\;\;\;r = 1\end{array}\)
\(OO' = \sqrt {{{(1 + 1)}^2} + {{( - 2 - 2)}^2}} = 2\sqrt 5 \Rightarrow OO' > r + r' \to \)
دو دایره مماس متخارجند
1736019749.png)
