شاه کلید نکات
شاه کلید سوال
1 با رسم شکل های مناسب به سؤال های زیر پاسخ دهید.
الف از یک نقطه چند خط می گذرد؟
ب از یک نقطه چند خط راست می گذرد؟
ج از دو نقطه چند خط (از انواع مختلف) می گذرد؟
د از دو نقطه چند خط راست می گذرد؟
الف بی شمار خط
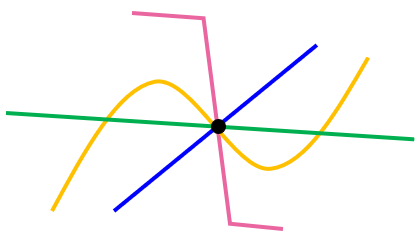
ب بی شمار خط
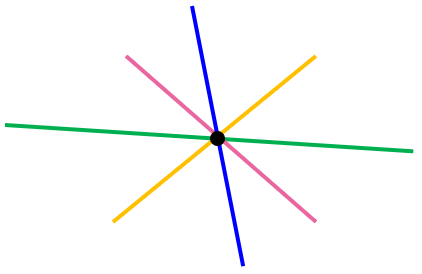
ج بی شمار خط (با انواع مختلف)
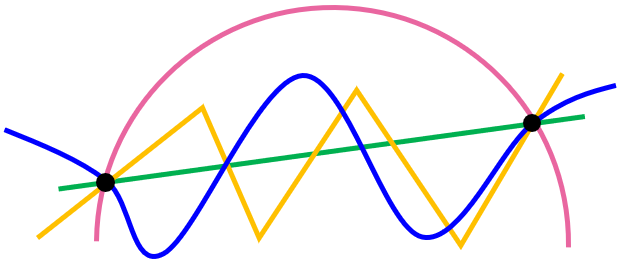
د فقط و فقط یک خط
2 یک خط رسم کنید و نقاط A، B، C و D را طوری روی آن نام گذاری کنید که رابطهٔ زیر درست باشد.
\(\overline {BD} - \overline {AD} = \overline {BC} + \overline {AC} \)
برای رسم این خط متغیر مربوط به طول پاره خط AD را هم به بعد از تساوی انتقال می دهیم تا به صورت مجموع تعدادی از پاره خط ها تبدیل شود:
\(\begin{array}{l}\overline {BD} - \overline {AD} = \overline {BC} + \overline {AC} \\\\ \Rightarrow \overline {BD} = \overline {BC} + \overline {AC} + \overline {AD} \end{array}\)
بنابراین پاره خط BD از مجموع پاره خط های BC، AC و AD تشکیل می یابد که نقاط B و D، نقاط دو سر پاره خط و نقاط A و C نیز، نقاط درون پاره خط هستند. پس یک پاره خط BD رسم می کنیم و دو نقطه بر روی این پاره خط مشخص می کنیم و آن ها را A و C نام گذاری می کنیم:
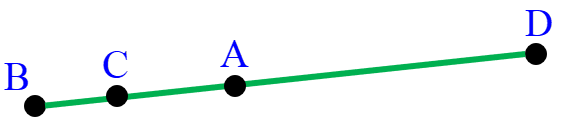
3 اگر روی یک خط راست ١٠ نقطه بگذارید، چند نیم خط به وجود می آید که سر آن ها روی این نقاط باشد؟ چرا؟
شکل زیر یک خط راست می باشد که روی آن 10 نقطه مشخص و نام گذاری کرده ایم:
حال تمام نیم خط هایی که از این 10 نقطه می توان بدست آورد را رسم می کنیم:
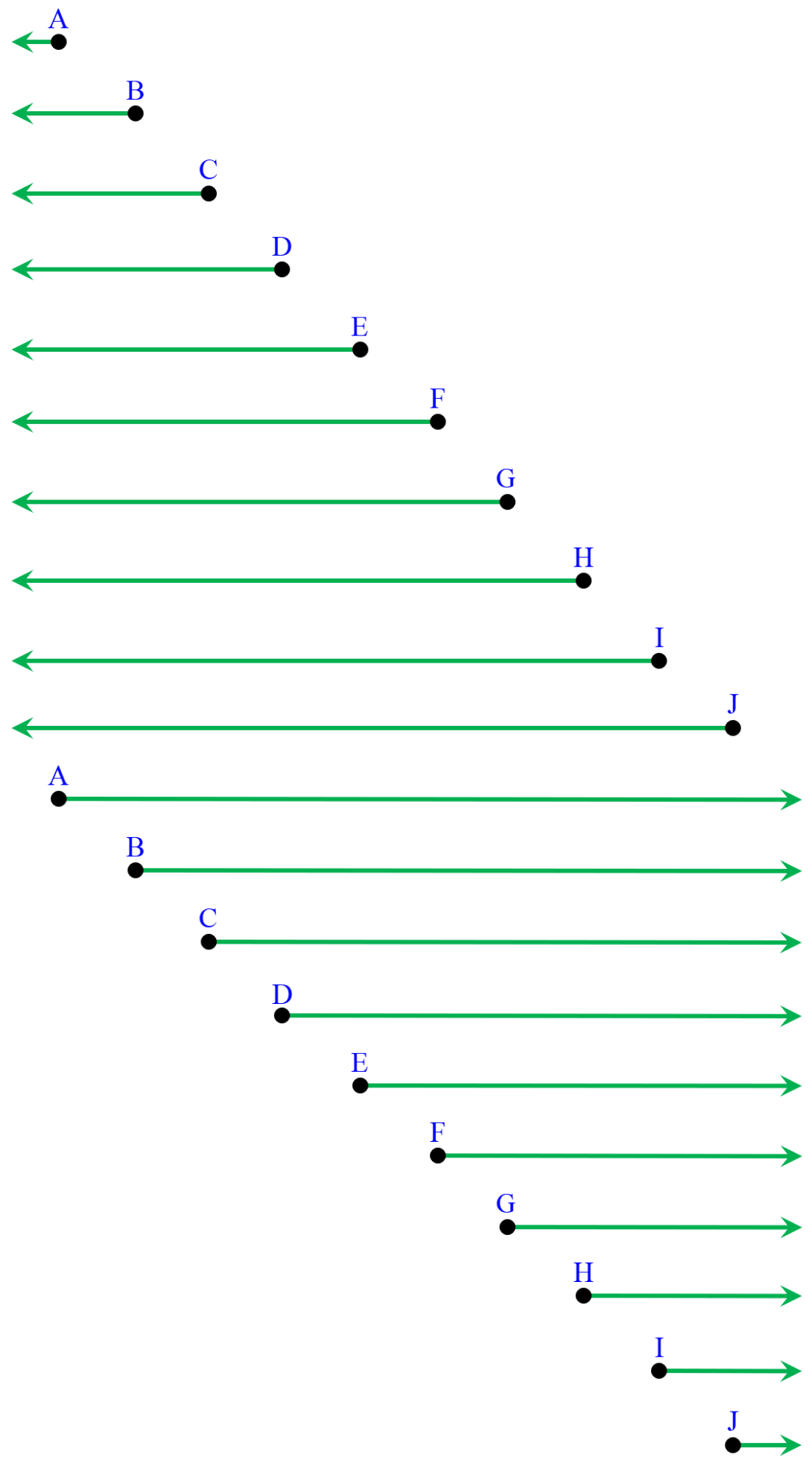
با توجه به شکل، هر نقطه با هر یک از دو سر خط، تشکیل دو نیم خط می دهند که در شکل مشخص شده است؛ ابتدا تمام نیم خط هایی که با این 10 نقطه و سر سمت چپ خط بدست می آیند را مشخص کرده ایم؛ سپس تمام نیم خط هایی را که با این 10 نقطه و این بار با سر سمت راست خط بدست می آیند را رسم کرده ایم. بنابراین خواهیم داشت:
20 = 10 × 2 = (تعداد نقطه ها) × 2 = تعداد نیم خط ها
4 نقطۀ C وسط پاره خط AB، نقطۀ D وسط پاره خط AC و نقطۀ E وسط پاره خط AD است.
\(\overline {AB} \)چند برابر \(\overline {AE} \)است؟
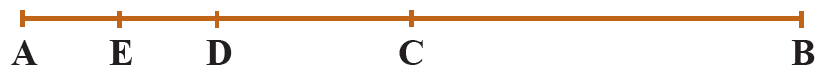
با توجه به متن مسئله، پاسخ می دهیم:
«نقطۀ C وسط پاره خط AB» یعنی:
\(\overline {AB} = 2\overline {AC} \)
«نقطۀ D وسط پاره خط AC» یعنی:
\(\overline {AC} = 2\overline {AD} \)
«نقطۀ E وسط پاره خط AD» یعنی:
\(\overline {AD} = 2\overline {AE} \)
بنابراین خواهیم داشت:
\(\begin{array}{l}\left\{ \begin{array}{l}\overline {AB} = 2\overline {AC} \\\\\overline {AC} = 2\overline {AD} \\\\\overline {AD} = 2\overline {AE} \end{array} \right.\\\\ \Rightarrow \overline {AB} = 2\overline {AC} = 2 \times (2\overline {AD} ) = 2 \times (2 \times (2\overline {AE} ))\\\\ \Rightarrow \overline {AB} = 8\overline {AE} \end{array}\)
پس پاره خط AB، 8 برابر پاره خط AE می باشد.
5 در شکل روبه رو یک مربع و یک مثلث متساوی الاضلاع دیده می شود.
چرا \(\,\overline {BE} = \overline {AC} \)؟
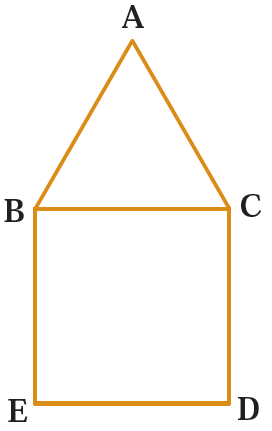
می دانیم که در هر مربع، اضلاع با هم برابر هستند و همچنین در مثلث متساوی الاضلاع نیز تمام اضلاع با هم برابرند؛ بنابراین تمام اضلاع و پاره خط های این شکل با هم برابر هستند:
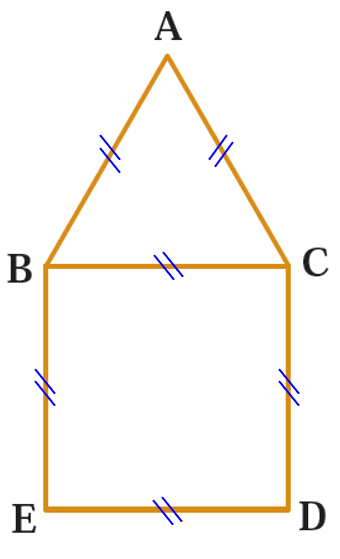
بنابراین داریم: \(\overline {BE} = \overline {AC} \)
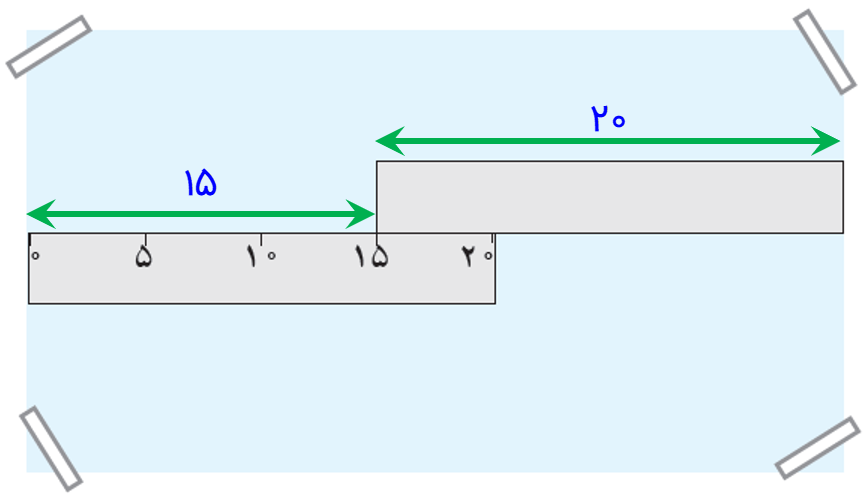
6 دو خط کش ٢٠ سانتی متری را مانند شکل رو به رو، روی یک صفحهٔ کاغذ قرار داده ایم. طول این صفحه چند سانتی متر است؟
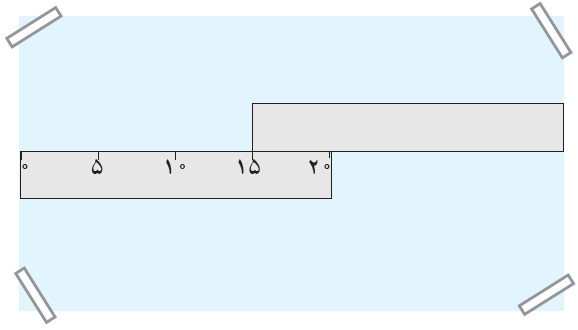
چون 5 سانتی متر از هر دو خط کش روی هم قرار گرفته است و مبدأ خط کش دوم روی 15 سانتی متری خط کش اول است، در نتیجه طول صفحه برابر است با 35 سانتی متر:
15 + 20 = 35
7 اندازهٔ قدّ علی را با a، اندازهٔ قدّ حسن را با b و اندازهٔ قدّ حسین را با c نشان می دهیم. رابطهٔ زیر را کامل کنید و نتیجه را به فارسی بنویسید.
\(\left. \begin{array}{l}a > b\\b = c\end{array} \right\} \Rightarrow \)
\(\left. \begin{array}{l}a > b\\b = c\end{array} \right\} \Rightarrow a > c\)
با توجه به اینکه قد علی از قد حسن بلندتر است و قد حسن با قد حسین برابر است، پس قد علی از قد حسین نیز بلندتر می باشد.
1736019749.png)
