جواب فعالیت صفحه 43 درس 4 ریاضی هفتم (هندسه و استدلال)
تعداد بازدید : 86.39Mپاسخ فعالیت صفحه 43 ریاضی هفتم
-گام به گام فعالیت صفحه 43 درس هندسه و استدلال
-فعالیت صفحه 43 درس 4
-شما در حال مشاهده جواب فعالیت صفحه 43 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
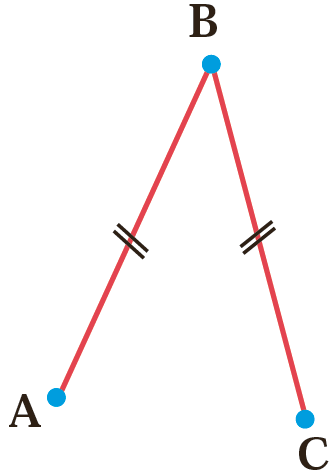
1 پاره خط های مساوی را به صورت روبه رو در شکل مشخص می کنیم.
علامت ها نشان می دهند که \(\overline {AB} = \overline {BC} \)
در شکل مقابل M وسط پاره خط AB است.
اندازهٔ کدام دو پاره خط مساوی است؟ ...... = ......

تساوی این دو پاره خط را با علامت گذاری روی شکل نشان دهید. تساوی های زیر را با نوشتن عدد مناسب کامل کنید.
\(\overline {AB} = \cdots \cdots \overline {AM} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline {AM} = \cdots \cdots \overline {AB} \)
\(\overline {AM} = \overline {MB} \)
\(\overline {AB} = 2\overline {AM} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline {AM} = \frac{1}{2}\overline {AB} \)
2 در شکل زیر پاره خط های\(DE\,,\,CD\,,\,BC\,,\,AB\) با هم مساوی اند. طول کدام پاره خط ها برابر \(3\overline {AB} \) است؟
طول کدام پاره خط ها برابر \(2\overline {AB} \) است؟
چند پاره خط در شکل روبه رو دیده می شود؟
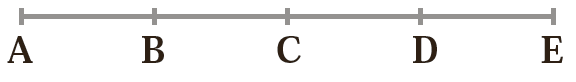
\(\overline {AD} = \overline {BE} = 3\overline {AB} \)
\(\overline {AC} = \overline {BD} = \overline {CE} = 2\overline {AB} \)
10 پاره خط وجود دارد:
AB – AC – AD – AE – BC – BD – BE – CD – CE – DE
3 با توجه به پاره خط هایی که در شکل زیر می بینید، اگر بدانیم\(\overline {EF} < \overline {GH} \,,\,\overline {DC} = \overline {EF} \,,\,\overline {AB} = \overline {DC} \) رابطه های زیر را کامل کنید. (علامت « \( \Rightarrow \) » یعنی نتیجه می گیریم)
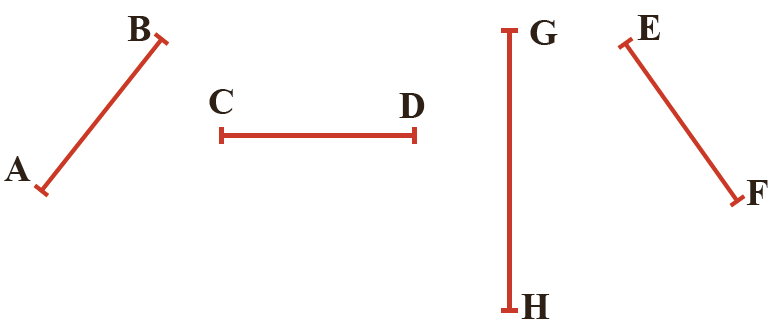
\(\begin{array}{l}\left. \begin{array}{l}\overline {AB} = \overline {DC} \\\overline {DC} = \overline {EF} \end{array} \right\} \Rightarrow \cdots \cdots = \cdots \cdots \\\\\left. \begin{array}{l}\overline {AB} = \overline {EF} \\\overline {EF} < \overline {GH} \end{array} \right\} \Rightarrow \cdots \cdots < \cdots \cdots \end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}\overline {AB} = \overline {DC} \\\overline {DC} = \overline {EF} \end{array} \right\} \Rightarrow AB = AF\\\\\left. \begin{array}{l}\overline {AB} = \overline {EF} \\\overline {EF} < \overline {GH} \end{array} \right\} \Rightarrow AB < GH\end{array}\)
4 مثلث ABC متساوی الساقین است؛ یعنی \(\overline {AB} = \overline {AC} \) نقطۀ M وسط AB و نقطۀ N وسط AC است.
چرا \(\,\overline {AN} = \overline {AM} \)؟
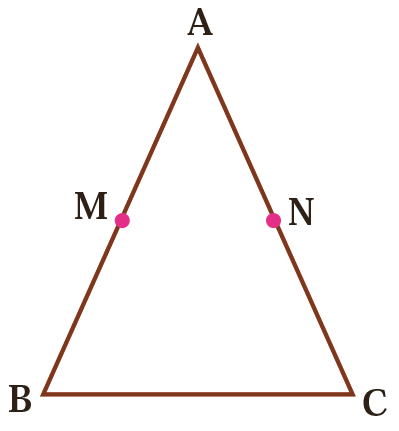
\(\overline {AB} = \overline {AC} \Rightarrow \frac{1}{2}\overline {AB} = \cdots \cdots \Rightarrow \cdots \cdots = \cdots \cdots \)
\(\overline {AB} = \overline {AC} \Rightarrow \frac{1}{2}\overline {AB} = \frac{1}{2}\overline {AC} \Rightarrow \overline {AM} = \overline {AN} \)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















