شاه کلید نکات
شاه کلید سوال
1 در مثلث متساوی الساقین مقابل، اندازهٔ ساق را با a و قاعده را با b نشان می دهیم.
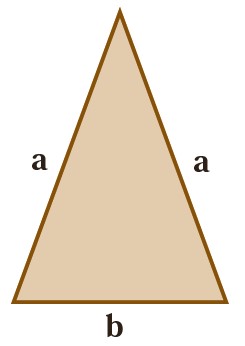
الف چرا هر دو ساق را با a نشان می دهیم؟
ب محیط مثلث را به دست آورید.
\( = P = \cdots + \cdots + \cdots \) محیط
ج مساحت مستطیل را با عبارت جبری بنویسید.
\( = S = \cdots \times \cdots \) مساحت
الف
به این دلیل که در مثلث متساوی الساقین اندازه ساق ها با هم برابر است؛ بنابراین اگر اندازه یکی از ساق ها a باشد، اندازه ساق دیگر نیز a خواهد بود.
ب
محیط مثلث برابر است با مجموع هر سه ضلع؛ بنابراین:
\( = P = a + a + b\) محیط
ج
مساحت مستطیل برابر است با طول × عرض؛ بنابراین:
\( = S = a \times b\) مساحت
2 هزینهٔ چاپ کارت ویزیت به این شرح حساب می شود : 3000 تومان قیمت پایه و 1000 تومان برای هر کارت. هزینهٔ چاپ n کارت چقدر می شود؟
ابتدا مقدار n را برابر 8 در نظر می گیریم. پاسخ را می یابیم؛ سپس الگوی کلی را می نویسیم:
\( = (3000 + (8 \times 1000))\) هزینه چاپ 8 کارت
\( = 3000 + 8000 = 11000\) تومان
حال به جای عدد 8، عبارت n را می گذاریم:
\( = (3000 + (n \times 1000))\) هزینه چاپ n کارت
\( = 3000 + 1000n\) تومان
3 حمید هر روز چند صفحه قرآن می خواند. اگر n تعداد صفحاتی باشد که حمید در یک روز می خواند، تعداد صفحاتی را که او در یک هفته می خواند، با یک عبارت جبری نشان دهید.
می دانیم که تعداد روزهای هفته، 7 روز می باشد. اگر تعداد صفحه های خوانده شده در یک هفته را x در نظر بگیریم، خواهیم داشت:
\( \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = \frac{{7 \times n}}{1} = 7 \times n = 7n\)
بنابراین حمید در یک هفته، به تعداد 7n صفحه قرآن می خواند.
4 هیئت مدیره مجتمع فرهنگی اردویی شهید باهنر تهران رابطه ای را برای نحوهٔ تعیین هزینه اردوهای دانش آموزی در این مرکز تعیین کرد. در این رابطه هزینه ورودی a تومان و به ازای هر دانش آموز b تومان دریافت می شود. اگر مدرسه ای n دانش آموز به اردوگاه بیاورد، هزینه اش از چه رابطه ای به دست می آید؟
در سال تحصیلی 1403 – 1402 قیمت ورودی مدرسه ٣٠٠٠٠٠ تومان و هزینه هر دانش آموز ٣٠٠٠٠ تومان است، در این صورت رابطه محاسبه هزینه در این سال تحصیلی را بنویسید.
تومان =a+b×n=a+bn هزینه اردوگاه برای n دانش آموز
به کمک جوابی که در قسمت اول سوال بدست آوردیم، قسمت دوم را حل می کنیم؛ فقط به جای هزینه اردوگاه، هزینه سال تحصیلی، به جای a عدد 300000 و به جای b عدد 30000 را قرار می دهیم تا جواب بدست آید:
تومان =300000+30000n هزینه سال تحصیلی برای n دانش آموز
5 جملۀ nام الگوهای زیر را بنویسید.
\(\begin{array}{l}4\,\,\,,\,\,\,8\,\,\,,\,\,\,12\,\,\,,\,\,\,16\,\,\,,\,\,\, \cdots \\\\1\,\,\,,\,\,\,\frac{1}{2}\,\,\,,\,\,\,\frac{1}{3}\,\,\,,\,\,\,\frac{1}{4}\,\,\,,\,\,\, \cdots \end{array}\)
\(4\,\,\,,\,\,\,8\,\,\,,\,\,\,12\,\,\,,\,\,\,16\,\,\,,\,\,\, \cdots \)
مقدار 4 از ضرب عدد 4 در 1 بدست می آید، مقدار عدد 8 از ضرب عدد 4 در عدد 2 بدست می آید. همین طور مقادیر 12 و 16 از ضرب عدد 4 در اعداد 3 و 4 بدست می آید. پس در ادامه برای بدست آوردن جملۀ n ام الگوی بالا، کافی است که عدد 4 را در n ضرب کرده تا جواب بدست آید؛ بنابراین:
\(\begin{array}{l}4 \times 1 = 4\\\\4 \times 2 = 8\\\\4 \times 3 = 12\\\\4 \times 4 = 16\\ \vdots \\4 \times n = 4n\\\\ \Rightarrow 4\,\,\,,\,\,\,8\,\,\,,\,\,\,12\,\,\,,\,\,\,16\,\,\,,\,\,\, \cdots \,\,\,,\,\,\,4n\end{array}\)
\(1\,\,\,,\,\,\,\frac{1}{2}\,\,\,,\,\,\,\frac{1}{3}\,\,\,,\,\,\,\frac{1}{4}\,\,\,,\,\,\, \cdots \)
اولین عدد از تقسیم عدد 1 بر 1 بدست می آید، دومین عدد از تقسیم عدد 1 بر 2 بدست می آید، سومین عدد از تقسیم عدد 1 بر 3 و چهارمین عدد از تقسیم عدد 1 بر 4 بدست می آید. پس در ادامه برای بدست آوردن جملۀ n ام الگوی بالا، کافی است که عدد 1 را بر n تقسیم کنیم تا جواب بدست آید؛ بنابراین:
\(\begin{array}{l}1 \div 1 = 1\\\\1 \div 2 = \frac{1}{2}\\\\1 \div 3 = \frac{1}{3}\\\\1 \div 4 = \frac{1}{4}\\ \vdots \\\\1 \div n = \frac{1}{n}\\\\ \Rightarrow 1\,\,\,,\,\,\,\frac{1}{2}\,\,\,,\,\,\,\frac{1}{3}\,\,\,,\,\,\,\frac{1}{4}\,\,\,,\,\,\, \cdots \,\,\,,\,\,\,\frac{1}{n}\end{array}\)
6 شکل nام چند چوب کبریت خواهد داشت؟
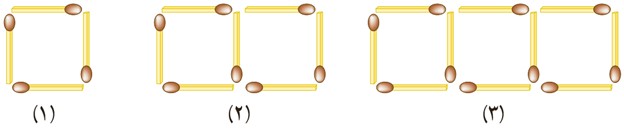
برای بدست آوردن تعداد چوب کبریت در شکل n ام کافی است که الگوی تعداد چوب کبریت ها را در هر شکل بدست آوریم. بنابراین با استفاده از راهبرد الگوی هندسی داریم:
4 = 1 × 3 + 1 = تعداد کبریت در شکل (1)
7 = 2 × 3 + 1 = تعداد کبریت در شکل (2)
10 = 3 × 3 + 1 = تعداد کبریت در شکل (3)
حال راحت می توانیم تعداد چوب کبریت در شکل n ام را بدست آوریم:
= تعداد چوب کبریت ها در شکل nام
\(1 + 3 \times n = 1 + 3n\)
7 اگر عدد x وارد نمودارهای روبه رو شود، چه عددی خارج خواهد شد؟ تفاوت این دو نمودار را توضیح دهید.
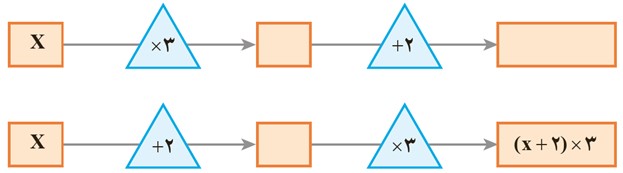
در نمودار بالایی در مستطیل کوچک عبارت 3x را می نویسیم؛ زیرا قبل از آن عدد x در عدد 3 ضرب شده است؛ سپس حاصل را با عدد 2 جمع می کنیم:
در نمودار پایینی در جای خالی عبارت x+2 را می نویسیم؛ زیرا قبل از آن عدد x با عدد 2 جمع شده است.
تفاوت این دو نمودار این است که اگر هر عددی به جای x قرار بگیرد، نتیجۀ خروجی این دو نمودار هرگز برابر نمی شوند. چرا که در نمودار اولی، عدد دلخواه ابتدا در عدد 3 ضرب شده، سپس با عدد 2 جمع شده است، اما در نمودار دومی، عدد دلخواه ابتدا با عدد 2 جمع می شود، سپس حاصل در عدد 3 ضرب می شود.
1736019749.png)
