1736019749.png)
جواب فعالیت صفحه 32 درس 3 ریاضی هفتم (جبر و معادله)
تعداد بازدید : 78.79Mپاسخ فعالیت صفحه 32 ریاضی هفتم
-گام به گام فعالیت صفحه 32 درس جبر و معادله
-فعالیت صفحه 32 درس 3
-شما در حال مشاهده جواب فعالیت صفحه 32 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 در بعضی از کشورها میوه را به صورت دانه ای می فروشند. اگر قیمت هر سیب را با a و قیمت هر گلابی را با b نشان دهیم، موارد زیر را با عبارت جبری نشان دهید.
قیمت 5 سیب:
قیمت 7 گلابی:
قیمت 3 سیب و 2 گلابی:
اگر فردی از میوه فروشی در یک روز 3 سیب و در روز بعد 2 سیب و 4 گلابی خریده باشد، مجموع هزینه این دو خرید چقدر می شود؟
= .............. + .............. = هزینه
قیمت 5 سیب:
\(a + a + a + a + a = 5 \times a = 5a\)
قیمت 7 گلابی:
\(b + b + b + b + b + b + b = 7 \times b = 7b\)
قیمت 3 سیب و 2 گلابی:
\(\left. \begin{array}{l}a + a + a = 3 \times a = 3a\\\\b + b = 2 \times b = 2b\end{array} \right\} \Rightarrow 3a + 2b\)
\( = 3a + 2a + 4b = 5a + 4b\) هزینه
2 الف مساحت هر دو مستطیل را با عبارت جبری نشان دهید.
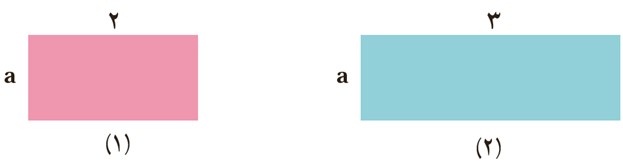
\({S_1} = \) مساحت مستطیل (1)
\({S_2} = \) مساحت مستطیل (2)
\(S = {S_1} + {S_2} = ......... + .........\)
ب دو مستطیل را کنار هم گذاشته ایم. توضیح دهید مساحت این شکل چگونه به دست آمده است؟
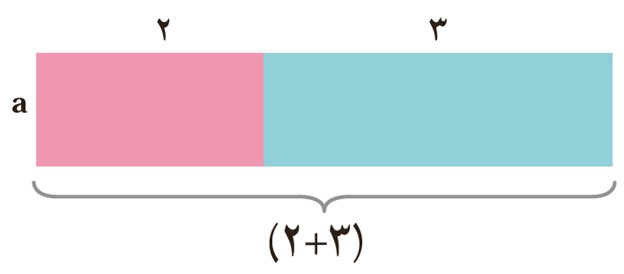
\(S = (2 + 3)a\)
ج پاسخ های الف و ب را با هم مقایسه کنید.
الف
\({S_1} = 2 \times a = 2a\) مساحت مستطیل (1)
\({S_2} = 3 \times a = 3a\) مساحت مستطیل (2)
\(S = {S_1} + {S_2} = 2a + 3a = 5a\)
ب
با کنار هم قرار دادن دو مستطیل کنار هم، مستطیل جدیدی به دست می آید که طول آن برابر است با مجموع دو مستطیل قبلی و عرض آن برابر است با عرض مستطیل های قبلی؛ بنابراین:
a = عرض مستطیل جدید
3 + 2 = طول مستطیل جدید
\( = (2 + 3) \times a = (2 + 3)a\) مساحت مستطیل جدید
ج
\(2a + 3a = (2 + 3)a = 5a\)
3 مانند سؤال 2 برای شکل زیر یک تساوی بنویسید.
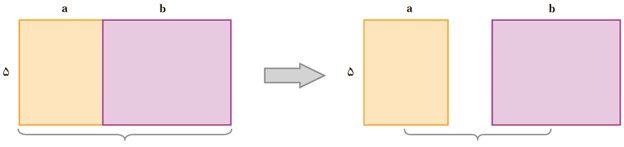
توضیح دهید که با کمک تساوی بالا چگونه می توان یک عدد بیرون پرانتز را در جمله های آن ضرب کرد.
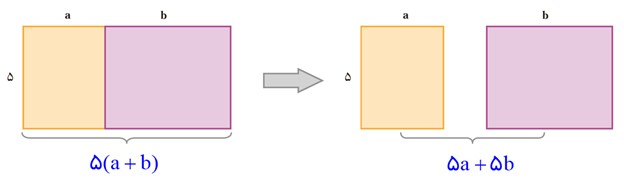
برای ضرب عدد بیرون پرانتز در جمله های داخل پرانتز، باید آن عدد را در تک تک جمله های داخل پرانتز ضرب کرد؛ برای مثال:
\(\begin{array}{l}a(b + c) = ab + ac\\\\2(b + c) = 2b + 2c\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
