جواب مرور فصل 3 صفحه 40 درس 3 ریاضی هفتم (جبر و معادله)

1 الگوی عددی

 «الگوی عددی» به مجموعه‌ای از اعداد (یا گاهیی شکل ها) گفته می‌شود که با یک نظم و قاعده‌ی مشخص و قابل پیش‌بینی پشت سر هم قرار گرفته‌اند. وظیفه‌ی تو به عنوان یک ریاضیدان، کشف این «قانون» پنهان است تا بتوانی اعداد بعدی الگو را حدس بزنی و حتی یک فرمول کلی (جملۀ nام) برای آن بنویسی.

مثال:

دنبالۀ 2 , 4 , 6 , 8 , …

تحلیل الگو: در این الگو، قانون این است که هر عدد 2 واحد از عدد قبلی خود بیشتر است.

2 عبارت جبری

«عبارت جبری» یک ابزار قدرتمند در ریاضی است! این عبارت شامل یک یا چند عدد، متغیر (حروف) و عمل های ریاضی (مثل جمع، تفریق، ضرب و تقسیم) است. در واقع، این راهی است برای نوشتن یک دستورالعمل ریاضی که مقادیر آن می‌توانند تغییر کنند.

مثال:

عبارت 2n-7 یا a+b

تحلیل عبارت 2n-7:

این عبارت می گوید که: «2 برابر یک عدد (n) منهای 7»

تحلیل عبارت a+b:

جمع دو عدد دلخواه

3 متغیر

«متغیر» یک نماد (معمولاً یکی از حروف الفبا مثل a یا x یا n) است که ما از آن به عنوان جانشین یک عدد استفاده می‌کنیم. این عدد یا مقداری است که هنوز آن را نمی‌دانیم (مجهول) یا مقداری است که می‌تواند تغییر کند (غیر مشخص).

مثال:

در فرمول محیط مربع P=4a

تحلیل متغیر:

در اینجا a یک متغیر است که نشان‌دهنده‌ی «طول ضلع» مربع است و P متغیر دیگری است که نشان‌دهنده‌ی «محیط» است.

4 جملات متشابه

«جملات متشابه» به جملاتی در یک عبارت جبری گفته می‌شود که قسمت حرفی (متغیر) آن‌ها دقیقاً یکسان باشد. تشخیص این جملات بسیار مهم است، چون ما فقط می‌توانیم جملات متشابه را با هم جمع یا از هم کم کنیم تا عبارت جبری را ساده کنیم.

مثال:

دو جمله‌ی 3a و 5a متشابه هستند.

تحلیل تشابه:

چون هر دو دارای متغیر a هستند، می‌توانیم آن‌ها را با هم جمع کنیم:

3a + 5a = 8a

اما جملۀ 3a با 5b متشابه نیست و نمی‌توان آن‌ها را با هم جمع کرد.

۱ نوشتن جملۀ nام یک الگو

این مهارت به تو کمک می‌کند تا بتوانی قانون و فرمول یک الگو را کشف کنی. به جای اینکه الگو را دانه به دانه ادامه دهی، یک فرمول جبری (بر حسب n) پیدا می‌کنی که n همان «شمارهٔ شکل» است.

مثال:

الگوی چوب کبریت ها:

3 , 5 , 7 , …

ما کشف کردیم که این الگو «۲ تا ۲ تا» زیاد می‌شود (پس 2n در کار است) و همیشه ۱ واحد هم بیشتر است.

جملۀ nام: 2n + 1

2 تبدیل عبارت‌های کلامی به عبارت‌های جبری

این یعنی بتوانی یک مسئله را از زبان فارسی به زبان جهانی ریاضی ترجمه کنی. در این ترجمه، کلماتی مثل «عددی» یا «مقداری» تبدیل به متغیر (مثل x) می‌شوند.

مثال:

عبارت کلامی «هشت واحد بیشتر از یک عدد»

• «یک عدد» را x می نامیم.
• «هشت واحد بیشتر» یعنی +8
• عبارت جبری: x+8

3 نوشتن محیط و مساحت شکل‌ها با عبارت جبری

به جای استفاده از عددهای ثابت، ما از متغیرها برای نوشتن فرمول‌های کلی محیط (دور تا دور) و مساحت (سطح) استفاده می‌کنیم.

مثال:

محیط مربع: اگر ضلع مربع a باشد، محیط آن P = a + a + a + a یا به صورت ساده ‌شده P = 4a است.

مساحت مستطیل: اگر طول و عرض a و b باشند، مساحت آن S = a × b است.

4 ساده کردن عبارت های درس با جمع و تفریق جملات متشابه

جملات متشابه، جملاتی هستند که قسمت حرفی (متغیر) آن‌ها دقیقاً یکی است (مثل 3a و 4a). ما فقط می‌توانیم این جملات را با هم جمع یا تفریق کنیم تا عبارت را خلاصه‌تر کنیم.

مثال:

ساده کردن 3a-8b+4a+6b:

3a با 4a متشابه است: 3a+4a=7a

-8b با 6b متشابه است: -8b+6b=-2b

شکل ساده شده: 7a-2b

5 ضرب عدد در پرانتز

این همان «خاصیت پخشی» یا توزیع‌پذیری است. عددی که بیرون پرانتز است، در تمام جملات داخل پرانتز، چه دو جمله باشند و چه بیشتر، ضرب می‌شود.

مثال:

\(\begin{array}{*{20}{r}}{2(3x + 5y)}\\{}\\{(2 \times 3x) + (2 \times 5y)}\end{array}\)

نتیجه: \(6x + 10y\)

6 ساده کردن عبارت و سپس محاسبهٔ مقدار عبارت جبری

این یک مهارت ترکیبی هوشمندانه است. به جای اینکه اعداد را در یک عبارت پیچیده و طولانی جای‌گذاری کنی، ابتدا عبارت را با استفاده از روش‌های (۴) و (۵) ساده می‌کنی و سپس اعداد را در عبارت ساده‌شده قرار می‌دهی. این کار هم سریع‌تر است و هم احتمال خطا را کم می‌کند.

مثال:

عبارت \(3(2x - 4y) - 5(x - 2y)\) را برای x = 2 و y = 3 حساب کنید.

1 ساده سازی:

\(\begin{array}{l}3(2x - 4y) - 5(x - 2y) = \\\\(6x - 12y) + ( - 5x + 10y) = \\\\(6x - 5y) + ( - 12y + 10y) = \\\\x - 2y\end{array}\)

2 محاسبه:

حالا x = 2 و y = 3 را در x – 2y می گذاریم:

\(\begin{array}{l}\left\{ \begin{array}{l}x = 2\\\\y = 3\end{array} \right.\\\\ \Rightarrow x - 2y = 2 - 2 \times 3 = \\\\2 - 6 = - 4\end{array}\)

7 پیدا کردن جواب معادله با حدس زدن

این یک راهبرد پایه‌ای برای درک مفهوم «جواب» است. تو عددهای مختلفی را به جای مجهول (x) حدس می‌زنی و آزمایش می‌کنی تا ببینی کدام عدد باعث می‌شود دو طرف تساوی برابر شوند.

مثال:

معادلۀ 8x – 7 = 17 

حدس اول: x = 2

8(2) – 7 = 16 – 7 = 9

حدس اول نادرست می باشد.

حدس دوم: x = 3

8(3) – 7 = 24 – 7 = 17

حدس دوم درست می باشد؛ پس x = 3 جواب معادله 8x – 7 = 17 می باشد.

8 تشکیل معادله و تبدیل مسئله های یک معادله

ین مهم‌ترین کاربرد جبر است: تبدیل یک مسئله‌ی داستانی (کلامی) به یک تساوی جبری (معادله). تو باید «خواستهٔ مسئله» یا مجهول را x بنامی و اطلاعات دیگر را بر اساس آن بچینی.

مثال:

محسن برای خرید ۸ مداد ۴۰۰۰۰ تومان داد و ۸۰۰۰ تومان پس گرفت. قیمت هر مداد چقدر است؟

مجهول (x): قیمت هر مداد

معادله: 8x + 8000 = 40000 (کل پول = پول باقی مانده + هزینه 8 مداد)

9 پیدا کردن مقدار عددی یک عبارت جبری

این فرآیند «جای‌گذاری» یا «جایگزینی» نام دارد. به تو یک عبارت جبری و مقادیر مشخصی برای متغیرها داده می‌شود. تو باید متغیرها را برداری و آن اعداد را به جایشان قرار دهی و حاصل را حساب کنی.

مثال:

مقدار a – (a – 2b) را به ازای a = 5 و b = 3 پیدا کنید.

جای گذاری:

5 – (5 – 2×3)

محاسبه (با رعایت ترتیب عملیات):

\(\begin{array}{l}5--(5--2 \times 3) = \\\\5--(5--6) = \\\\5 - ( - 1) = \\\\5 + 1 = 6\end{array}\)

10 مفهوم معادله و جواب معادله

معادله:

یک تساوی جبری است (یعنی حتماً علامت = دارد) که فقط به ازای مقادیر خاصی از متغیر، برقرار است.

جواب:

همان «مقدار خاصی» است که اگر به جای متغیر در معادله بگذاریم، تساوی را برقرار می‌کند (دو طرف مساوی می‌شوند).

مثال:

در معادلۀ 4n + 7 = 27:

عدد n = 5 جواب معادله است، چون:

4(5) + 7 = 20 + 7 = 27

تساوی برقرار است.

عدد n = 3 جواب نیست، چون:

4(3) + 7 = 12 + 7 = 19

که مساوی 27 نیست.

11 روش حل معادله

این روش اصولی و قدرتمند (برخلاف حدس زدن) برای پیدا کردن جواب است. هدف ما «تنها کردن مجهول (x)» است. برای این کار، از عملیات معکوس استفاده می‌کنیم (مثلاً 1- را با 1+ خنثی می‌کنیم) و هر کاری را روی هر دو طرف تساوی انجام می‌دهیم تا تعادل حفظ شود (مثل یک ترازو).

مثال:

حل معادلۀ 2x – 1 = 7

1 خنثی کردن -1 :

1+ را به هر دو طرف اضافه می‌کنیم:

\(\begin{array}{l}2x - 1 = 7\\\\\mathop \Rightarrow \limits^{( + 1)} 2x - 1 + 1 = 7 + 1\\\\ \Rightarrow 2x = 8\end{array}\)

که می شود 2x = 8

2 خنثی کردن ضرب‌ در ۲:

هر دو طرف را بر ۲ تقسیم می‌کنیم:

\(\begin{array}{l}2x = 8\\\\\mathop \Rightarrow \limits^{( \times \frac{1}{2})} 2x \times \frac{1}{2} = 8 \times \frac{1}{2}\\\\ \Rightarrow \frac{{2x}}{2} = \frac{8}{2}\\\\ \Rightarrow x = 4\end{array}\)

جواب معادلۀ بالا برابر با x = 4 شد.

\(\begin{array}{l}3(2x - y + 1) - 4x + y - 3 - (2x - y - 7) = \\\\6x - 3y + 3 - 4x + y - 3 - 2x + y + 7 = \\\\(6x - 4x - 2x) + ( - 3y + y + y) + (3 - 3 + 7) = \\\\0 - y + 7\\\\ - y + 7\\\\\left\{ \begin{array}{l}x = - 1\\\\y = - 2\end{array} \right.\\\\ \Rightarrow 3(2x - y + 1) - 4x + y - 3 - (2x - y - 7) = \\\\ - y + 7 = - ( - 2) + 7 = 2 + 7 = 9\end{array}\)

\(\begin{array}{l}2x - 3x + 2(x + 2) = 14\\\\ \Rightarrow 2x - 3x + 2x + 4 = 14\\\\ \Rightarrow x + 4 = 14\\\\\mathop \Rightarrow \limits^{( - 4)} x + 4 - 4 = 14 - 4\\\\ \Rightarrow x = 10\end{array}\)

ابتدا باید مشخص کنیم که این فرد چه مقدار کالری باید بسوزاند تا 1/8 کیلوگرم از وزنش کم بشود.

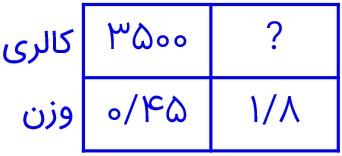
\( \Rightarrow ? = \frac{{3500 \times 1/8}}{{4/5}} = 1400\)

حالا مشخص است که این میزان کالری باید در 2 هفته یعنی 14 روز سوزانده شود، پس باید بیابیم که در هر چه مقدار کالری سوزانده شود:

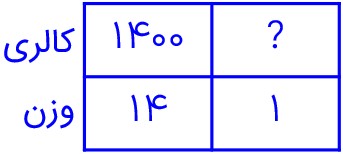
\( \Rightarrow ? = \frac{{1400 \times 1}}{{14}} = 100\)

100 کالری که باید در هر روز سوزانده شود.

کدام عدد صحیح است که اگر از دو برابر آن، یک واحد کم کنیم، حاصل برابر با 7 می شود؟

\(\begin{array}{l}2x - 1 = 7\\\\\mathop \Rightarrow \limits^{( + 1)} 2x - 1 + 1 = 7 + 1\\\\ \Rightarrow 2x = 8\\\\\mathop \Rightarrow \limits^{( \times \frac{1}{2})} 2x \times \frac{1}{2} = 8 \times \frac{1}{2}\\\\ \Rightarrow \frac{{2x}}{2} = \frac{8}{2}\\\\ \Rightarrow x = 4\end{array}\)