جواب تمرین صفحه 47 درس 4 ریاضی هفتم (هندسه و استدلال)
تعداد بازدید : 86.39Mپاسخ تمرین صفحه 47 ریاضی هفتم
-گام به گام تمرین صفحه 47 درس هندسه و استدلال
-تمرین صفحه 47 درس 4
-شما در حال مشاهده جواب تمرین صفحه 47 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
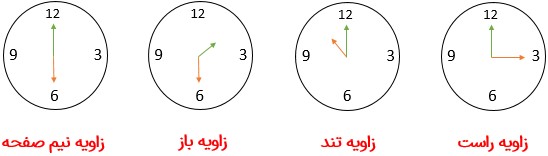
1 یک مثال برای هریک از زمان هایی بنویسید که عقربهٔ بین ساعت شمار و دقیقه شمار زاویهٔ راست، باز، تند و نیم صفحه را نشان دهد.
2 اندازهٔ زاویه های x و y را در شکل های زیر پیدا کنید.
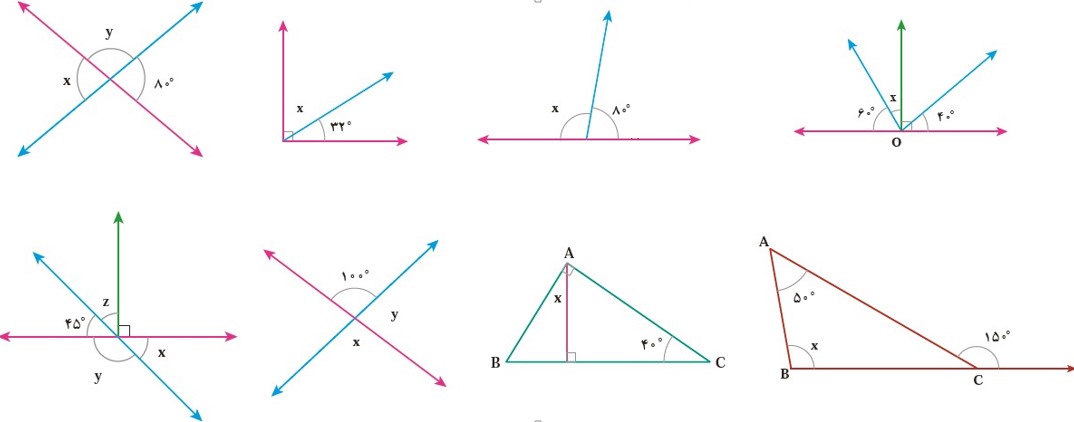
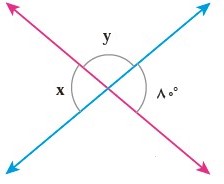
\(y + {80^ \circ } = {180^ \circ }\, \Rightarrow \,y = {180^ \circ } - {80^ \circ } = {100^ \circ }\)
به دلیل این که زاویه \(x\) با \({80^ \circ }\) متقابل به راستند از این رو :
\(x = {80^ \circ }\,\)
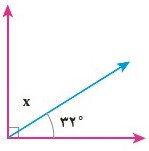
\(x + {32^ \circ } = {90^ \circ } \Rightarrow x = {90^ \circ } - {32^ \circ } = {58^ \circ }\)
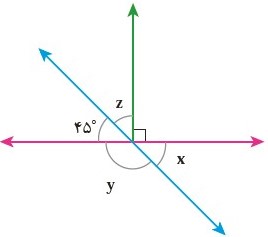
\(z + {45^ \circ } = {90^ \circ } \Rightarrow z = {90^ \circ } - {45^ \circ } = {45^ \circ }\)
زاویه \(x\) با زاویه \({45^ \circ }\) متقابل به راس است از این رو \(X = {45^ \circ }\)
\(x + y = {180^ \circ } \Rightarrow {45^ \circ } + y = {180^ \circ } \Rightarrow y = {180^ \circ } - {45^ \circ } = {135^ \circ }\)
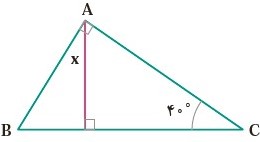
\(\hat b = {180^ \circ } - \left( {{{40}^ \circ } + {{90}^ \circ }} \right) = {180^ \circ } - {130^ \circ } = {50^ \circ }\)
\(x = {180^ \circ } - \left( {{{90}^ \circ } - \hat b} \right) = {180^ \circ } - {140^ \circ } = {40^ \circ }\)
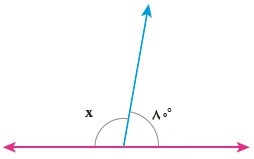
\(x + {80^ \circ } = {180^ \circ } \Rightarrow x = {180^ \circ } - {80^ \circ } = {100^ \circ }\)
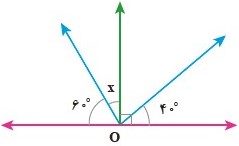
\(x + {60^ \circ } = {90^ \circ } \Rightarrow x = {90^ \circ } - {60^ \circ } = {30^ \circ }\)
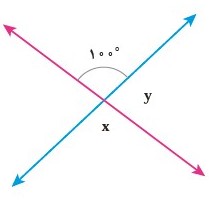
\(y + {100^ \circ } = {180^ \circ } \Rightarrow y = {180^ \circ } - {100^ \circ } = {80^ \circ }\)
زاویه \(x\) با زاویه \({100^ \circ }\) متقابل به راس است از این رو \(x = {100^ \circ }\)
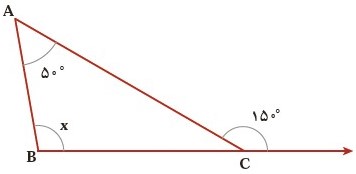
\(\hat c = {180^ \circ } - {150^ \circ } = {30^ \circ }\)
\(x = {180^ \circ } - \left( {\hat c + {{50}^ \circ }} \right) = {180^ \circ } - {80^ \circ } = {100^ \circ }\)
3 در شکل مقابل می دانیم زاویه های \({90^ \circ }\,,\,t\hat Oy\,,\,x\hat Oz\) هستند.
چگونه می توانید نتیجه بگیرید که: \(\,x\hat Oy\, = \,t\hat Oz\) ؟
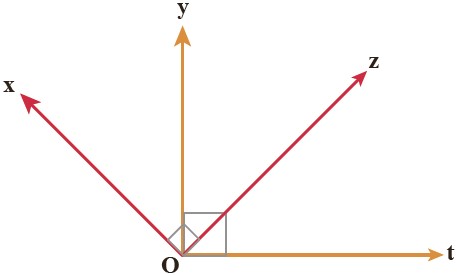
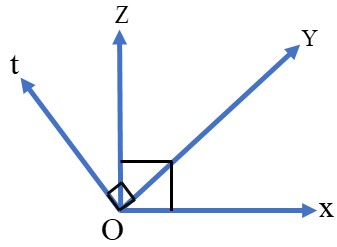
\(\left. \begin{array}{l}x\hat Oy + y\hat Oz = 90 \Rightarrow x\hat Oz\\z\hat Ot + y\hat Oz = 90 \Rightarrow y\hat Ot\end{array} \right\} \Rightarrow x\hat Oy = z\hat Ot\)
4 در شکل مقابل اندازهٔ زاویهٔ \(\,x\hat Az\,\) برابر 120 درجه است.
زاویهٔ \(\,x\hat Ay\) چه کسری از \(\,x\hat Az\,\) است؟
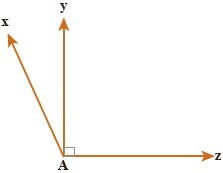
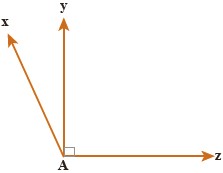
\(\begin{array}{l}x\hat Ay = {120^ \circ } - {90^ \circ } = {60^ \circ }\\x\hat Ay = \frac{{{{30}^ \circ }}}{{{{120}^ \circ }}}x\hat Az = \frac{1}{4}x\hat Az\end{array}\)
5 شکل های زیر چه شباهت هایی با هم دارند؟ چه تفاوت هایی با هم دارند؟
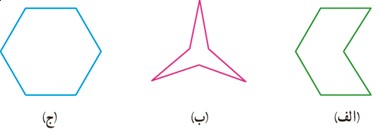
شکل های الف و ب هر دو جزء چند ضلعی های مقعر هستند چون دارای زوایای بزرگتر از \({180^ \circ }\) هستند.
شکل ج جزء چندضلعی های منتظم است و همچنین چندضلعی مقعر نیز می باشد.
در هر سه شکل همه اضلاع با هم برابرند .
در هر سه شکل زاویه باز وجود دارد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















