1736019749.png)
جواب تمرین صفحه 139 درس 6 ریاضی دهم (شمارش، بدون شمردن)
تعداد بازدید : 78.77Mپاسخ تمرین صفحه 139 ریاضی دهم
-گام به گام تمرین صفحه 139 درس شمارش، بدون شمردن
-تمرین صفحه 139 درس 6
-شما در حال مشاهده جواب تمرین صفحه 139 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 یک فروشندهٔ تنقلات در فروشگاه خود، پسته، بادام، گردو، تخمهٔ کدو، تخمهٔ ژاپنی، نخودچی و کشمش دارد. از نظر او در یک آجیل حداقل پنج نوع از تنقلات فوق باید وجود داشته باشد. او با تنقلات موجود در فروشگاهش چند نوع آجیل می تواند درست کند؟
\(\left( {\begin{array}{*{20}{c}}7\\5\end{array}} \right) + \left( {\begin{array}{*{20}{c}}7\\6\end{array}} \right) + \left( {\begin{array}{*{20}{c}}7\\7\end{array}} \right) = 28 + 7 + 1 = 36\)
2 یک اداره دارای 18 عضو است. این اداره دارای 1 رئیس، 3 معاون، 2 حسابدار، 6 کارشناس اداری، 3 کارمند کارگزینی و 3 کارشناس امور حقوقی است. این اداره ماهانه باید جلسه ای 5 نفره جهت بررسی و تصویب آخرین طرح های پیشنهادی برگزار کند. به چند طریق این گروه 5 نفره می تواند انتخاب شود، هرگاه:
الف رئیس و دقیقاً یک کارشناس امور حقوقی در جلسه باشند؟
ب رئیس و دقیقاً یک معاون و یک کارشناس امور حقوقی در جلسه باشند؟
پ رئیس و دقیقاً یک معاون، یک حسابدار و یک کارشناس امور حقوقی در جلسه باشند؟
الف
ب
پ
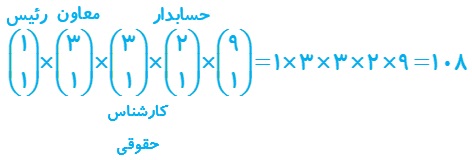
3 در یک کلاس تعدادی از دانش آموزان که همگی دارای شرایط علمی خوبی اند، داوطلب حضور در مسابقات علمی مدرسه هستند. معلم قصد دارد 2 نفر را به تصادف انتخاب کند. او این دو نفر را به 28 روش می تواند از بین داوطلبان انتخاب کند. تعداد داوطلبان چند نفر بوده است؟
فرض کنیم تعداد داوطلبان n نفر باشند؛ بنابراین:
\(\left( {\begin{array}{*{20}{c}}n\\2\end{array}} \right) = 28 \Rightarrow \frac{{n\left( {n - 1} \right)}}{2} = 28 \Rightarrow n\left( {n - 1} \right) = 56 = 8\: \times \:7 \Rightarrow n = 8\)
4 گل فروشی در فروشگاه خود 10 نوع گل مختلف دارد. او در هر دسته گل از 3 تا 5 شاخه گل متمایز قرار می دهد. او چند دسته گل مختلف می تواند درست کند؟
\(\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{10}\\5\end{array}} \right) = 120 + 210 + 252 = 582\)
5 یک نقاش قوطی هایی از 4 رنگ قرمز، آبی، زرد و مشکی دارد. اگر او با ترکیب دو یا چند قوطی از رنگ های متمایز بتواند دقیقاً یک رنگ جدید به دست آورد، او چند رنگ می تواند داشته باشد؟ چرا با اینکه در کارهای هنری فقط از همین 4 رنگ استفاده می شود، اما تعداد رنگ های حاصل بیشتر از جواب شماست؟
\(\left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) + \left( {\begin{array}{*{20}{c}}4\\3\end{array}} \right) + \left( {\begin{array}{*{20}{c}}4\\4\end{array}} \right) = 6 + 4 + 1 = 11\)
چون ممکن است میزان ترکیب رنگ ها یکسان نباشد، به طور مثال یک بار 50% از یک رنگ و 50% از رنگ دیگر استفاده شود و بار دیگر 60% از یکی و 40% از دیگری استفاده شود ودر این حالت دو رنگ متفاوت بدست آید.
6 هفت نقطهٔ A و B و C و D و F و G روی محیط یک دایره قرار دارند. چند مثلث مختلف می توان کشید که رئوس آن از این هفت نقطه انتخاب شده باشند؟
\(\left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = \frac{{7!}}{{3!\: \times \:4!}} = 35\)
7 یک آشپز ده نوع ادویه دارد. او با استفاده از هر 3 تا از این ادویه ها یک طعم مخصوص درست می کند. این آشپز چند طعم می تواند درست کند هرگاه
الف هیچ محدودیتی در استفاده از ادویه ها نداشته باشد؟
ب دو نوع ادویه هستند که با هم نمی توانند استفاده شوند؟
پ سه ادویه هستند که نباید هر سه با هم استفاده شوند؟
ت ادویه ها به 2 دسته 5 تایی تقسیم می شوند که هیچ یک از ادویه های دسته اول با هیچ یک از ادویه های دسته دوم سازگاری ندارند؟
الف
\(\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) = \frac{{10!}}{{3!\: \times \:7!}} = 120\)
ب تعداد حالاتی که دو ادویه با هم استفاده می شوند – تعداد کل حالات = تعداد حالاتی که دو ادویه با هم استفاده نمی شوند
\( = \left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) - \left( {\begin{array}{*{20}{c}}8\\1\end{array}} \right) = 120 - 8 = 112\)
پ تعداد حالاتی که سه ادویه با هم استفاده می شوند – تعداد کل حالات = تعداد حالاتی که هر سه ادویه استفاده نمی شوند
\( = \left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) - \left( {\begin{array}{*{20}{c}}3\\3\end{array}} \right) = 120 - 1 = 119\)
ت هر سه ادویه باید از دسته اول انتخاب شده یا هر سه ادویه از دسته دوم انتخاب شوند؛ بنابراین :
\(\left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) = 10 + 10 = 20\)
8 مسئله ای طرح کنید که جواب آن برابر باشد با:
الف \(\left( \begin{array}{l}5\\3\end{array} \right) \times \left( \begin{array}{l}6\\2\end{array} \right)\)
ب \(\left( \begin{array}{l}5\\3\end{array} \right) + \left( \begin{array}{l}6\\2\end{array} \right)\)
الف به چند طریق می توان از بین 5 مهره آبی و 6 مهره قرمز ، 5 مهره انتخاب کرد به طوری که 2 مهره آبی و 3 مهره قرمز وجود داشته باشد؟
\(\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\3\end{array}} \right) = 10\: \times \:20 = 200\)
ب احسان می خواهد با پول های قُلّکش 2 مداد یا 3 پاک کن (فقط یکی از این دو نوع) را خریداری کند. اگر در مغازه لوازم التحریر فقط 6 نوع مداد و 5 نوع پاک کن مختلف موجود باشد، احسان چند انتخاب برای خرید دارد؟
\(\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) + \left( {\begin{array}{*{20}{c}}6\\3\end{array}} \right) = 10\: + \:20 = 30\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
