جواب تمرین صفحه 115 درس 5 ریاضی دهم (تابع)
تعداد بازدید : 86.34Mپاسخ تمرین صفحه 115 ریاضی دهم
-گام به گام تمرین صفحه 115 درس تابع
-تمرین صفحه 115 درس 5
-شما در حال مشاهده جواب تمرین صفحه 115 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 تابع f(x) = 3x-1 را که دامنهٔ آن مجموعه \(\left( {\frac{1}{2},0,5} \right)\) است، رسم کنید. برد این تابع را به دست آورید و نمایش زوج مرتبی و نمودار پیکانی آن را ارائه دهید. اگر دامنهٔ این تابع R باشد، پاسخ ها چگونه خواهد بود؟

\(\begin{array}{*{20}{l}}{f\left( x \right) = 3x - 1}\\{f\left( 0 \right) = - 1\;\;\:,\;\;\:f\left( {\frac{1}{2}} \right) = \frac{1}{2}\;\;\:,\;\;\:f\left( 5 \right) = 14}\\{R = \left\{ { - 1\:,\:\frac{1}{2}\:,\:14} \right\}}\\{f = \left\{ {\left( {0\:,\: - 1} \right)\:,\:\left( {\frac{1}{2}\:,\:\frac{1}{2}} \right)\:,\:\left( {5\:,\:14} \right)} \right\}}\end{array}\)

اگر دامنه R باشد، داریم:

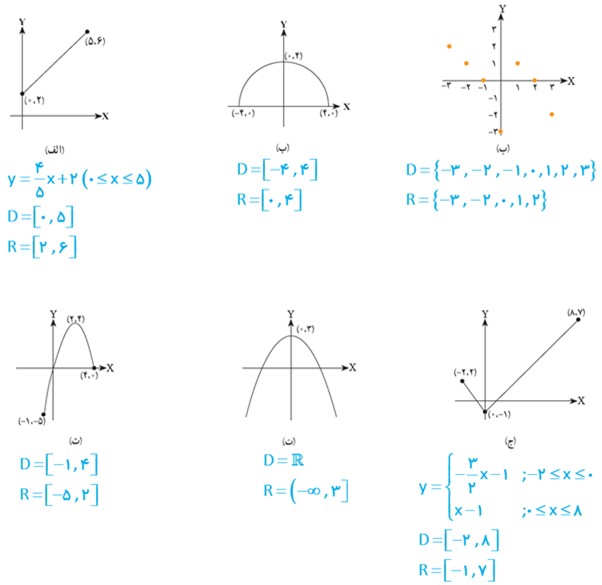
2 در شکل های زیر نمودار تعدادی از توابع رسم شده اند. دامنه و برد هر یک از این توابع را به کمک نمودار آنها مشخص کنید. در هر مورد که امکان دارد، دامنه و برد را به صورت یک بازه نمایش دهید. نمایش جبری توابع (الف) و (ج) را بنویسید.

3 درستی یا نادرستی گزاره های زیر را بررسی کنید.
الف دامنهٔ تابع \(f(x) = {x^2} - 1\) برابر \(\left( {0, + \infty } \right)\) و بُرد آن نیز \(\left( {0, + \infty } \right)\) است.
ب دامنهٔ تابع \(f(x) = \left| x \right| - \frac{1}{3}\) همهٔ اعداد حقیقی و بُرد آن \(\left( {2, + \infty } \right)\) است.
پ دامنهٔ تابع ثابت f(x) = 2 برابر \(\left( { - \infty , + \infty } \right)\) است.
ت اگر f(x) = 2x + 1 آنگاه، \(f(1) = \frac{{f(2)}}{2}\)
الف
نادرست؛ زیرا: \(D = \mathbb{R}\;\;,\;\;R = \left[ {\left. { - 1\:,\:\infty } \right)} \right.\)
ب
نادرست؛ زیرا: \(R = \left[ {\left. { - \frac{1}{3}\:,\:\infty } \right)} \right.\)
پ
درست.
ت
نادرست.
4 یک تانکر گاز از یک استوانه و دو نیم کره به شعاع r در دو انتهای استوانه، تشکیل شده است. اگر ارتفاع استوانه 30 متر باشد، حجم تانکر را بر حسب تابعی از r بنویسید.
حجم دو نیمکره با حجم یک کره برابر است؛ درنتیجه حجم کل برابر با مجموع حجم استوانه و حجم کره است:
\(\left. {\begin{array}{*{20}{l}}{{V_{Sphere}} = \frac{4}{3}\pi {\mkern 1mu} {r^3}}\\{{V_{cylinder}} = \pi {\mkern 1mu} {r^2} \times 30}\end{array}} \right\} \Rightarrow V = \frac{4}{3}\pi {\mkern 1mu} {r^3} + 30\pi {\mkern 1mu} {r^2}\)
5 هریک از نمودارهای زیر کدام یک از تابع های (الف) تا (ر) را نمایش می دهد؟ دامنه و برد این توابع چیست؟

\(y = {x^2} - 3\) الف
\(y = - {x^2} + 2\) ب
\(y = \left| x \right|\) پ
\(y = - \left| x \right|\) ت
\(y = {\left( {x + 1} \right)^2}\) ث
\(y = \left| x \right| - \frac{1}{2}\) ج
\(y = \left| {x - 2} \right|\) چ
\(y = - {\left( {x + 2} \right)^2}\) ح
\(y = - \left| x \right| - 2\) خ
\(y = {\left( {x - 2} \right)^2} + 3\) د
\(y = \left| x \right| - 2\) ذ
\(y = {\left( {x + \frac{1}{2}} \right)^2} - 3\) ر

6 فرض کنیم دامنهٔ هریک از توابع تمرین ٥ به بازهٔ [-2, 3] محدود شده باشد. در این صورت برد هر تابع را پیدا کنید. از نمودارها کمک بگیرید.
الف
\(y = {x^2} - 3\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {0\:,\:6} \right]{\mkern 1mu} }\end{array}\)
ب
\(y = - {x^2} + 2\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 7\:,\:2} \right]{\mkern 1mu} }\end{array}\)
پ
\(y = \left| x \right|\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {0\:,\:3} \right]{\mkern 1mu} }\end{array}\)
ت
\(y = - \left| x \right|\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 3\:,\:0} \right]{\mkern 1mu} }\end{array}\)
ث
\(y = {\left( {x + 1} \right)^2}\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {0\:,\:16} \right]{\mkern 1mu} }\end{array}\)
ج
\(y = {\left( {x + 1} \right)^2}\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {0\:,\:\frac{5}{2}} \right]{\mkern 1mu} }\end{array}\)
چ
\(y = \left| {x - 2} \right|\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {0\:,\:4} \right]{\mkern 1mu} }\end{array}\)
ح
\(y = - {\left( {x + 2} \right)^2}\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 25\:,\:0} \right]{\mkern 1mu} {\mkern 1mu} }\end{array}\)
خ
\(y = - \left| x \right| - 2\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 5\:,\: - 2} \right]{\mkern 1mu} }\end{array}\)
د
\(y = {\left( {x - 2} \right)^2} + 3\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ {3\:,\:17} \right]{\mkern 1mu} }\end{array}\)
ذ
\(y = \left| x \right| - 2\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 2\:,\:1} \right]{\mkern 1mu} }\end{array}\)
ر
\(y = {\left( {x + \frac{1}{2}} \right)^2} - 3\)
\(\begin{array}{*{20}{l}}{D = \left[ { - 2\:,\:3} \right]\:}\\{R = \left[ { - 3\:,\:\frac{{37}}{4}} \right]{\mkern 1mu} }\end{array}\)
7 نمودار تابع f داده شده است. ضابطهٔ این تابع را بنویسید و مقادیر خواسته شده را حساب کنید.

\(\begin{array}{l}f\left( {\sqrt 5 } \right)\;\;\;f\left( 6 \right)\;\;\;f\left( 3 \right)\\\\f\left( {\frac{1}{2}} \right)\;\;\;f\left( 0 \right)\;\;\;f\left( { - \frac{5}{2}} \right)\end{array}\)
\(\begin{array}{l}f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} - 2\;\;\:\;\;\:\;\;\:\:\:;x \le - 3\\\end{array}\\\begin{array}{l}5x + 13\;\;\:\:\:{\mkern 1mu} ; - 3 < x \le - 2\\\end{array}\\\begin{array}{l} - \frac{3}{4}x + \frac{3}{2}\;\;\:; - 2 < x \le 2\\\end{array}\\{4x - 8\;\;\:\;\;\:{\mkern 1mu} ;2 < x \le 3}\end{array}} \right.\\\\f\left( {\sqrt 5 } \right) = 4\sqrt 5 - 8\\\\f\left( 6 \right) \otimes \\\\f\left( 3 \right) = 4\\\\f\left( {\frac{1}{2}} \right) = \frac{{21}}{8}\\\\f\left( 0 \right) = \frac{3}{2}\\\\f\left( { - \frac{5}{2}} \right) = \frac{1}{2}\end{array}\)
8 نمودار یک تابع خطی از نقاط (4,3) و (0,3) می گذرد. F(-4) و f(-1) را به دست آورید.
\(\begin{array}{*{20}{l}}\begin{array}{l}f\left( x \right) = ax + b\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}f\left( 4 \right) = 3 = 4a + b\\\end{array}\\{f\left( 0 \right) = 3 = b \Rightarrow a = 0}\end{array}} \right. \Rightarrow f\left( x \right) = 3\\\end{array}\\{ \Rightarrow f\left( { - 4} \right) = f\left( { - 1} \right) = 3}\end{array}\)
9 هزینهٔ مکالمهٔ تلفنی با کشور دیگر، از زمان برقراری تماس برای 3 دقیقه یا کمتر، 2هزار تومان است و پس از آن برای هر دقیقه یک هزارتومان به هزینهٔ آن اضافه می شود. مثلاً برای زمان بیشتر از 3 دقیقه تا دقیقاً 4 دقیقه، 3 هزار تومان دریافت می شود. نمودار هزینه را برحسب زمان تا پایان زمان 6 دقیقه رسم کنید.
\(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}2,000\;\;\:\;\;\:\;\;\:\:\:;0 < x \le 3\\\end{array}\\{1,000x - 1,000\;\;\:\:\:{\mkern 1mu} ;3 < x}\end{array}} \right.\)

10 کدام یک از رابطه های زیر یک تابع را نمایش می دهد؟ چرا؟ نمودار هر دو معادله را رسم کنید.
\(\begin{array}{l}f\left( x \right) = \left\{ \begin{array}{l}x\;\;\;\;\;\;\;\;x > 0\\\\x + 2\;\;\;\;x \le 2\end{array} \right.\\\\g\left( x \right) = \left\{ \begin{array}{l}2x\;\;\;\;\;\;x < 0\\\\x + 1\;\;\;\;x \ge 0\end{array} \right.\end{array}\)

11 الگوی زیر از تعدادی ذوزنقه تشکیل شده است.

الف جدول زیر را کامل کنید.

ب چرا رابطهٔ بین تعداد ذوزنقه ها و محیط شکل، یک تابع را معلوم می کند؟ دامنه و برد این تابع چیست؟ نمودار آن را رسم کنید.
الف

ب
به این دلیل که هیچ یک از مؤلفه های اول آن تکرار نشده است. یا به عبارتی دیگر، هر مؤلفه اول، فقط و فقط یک مقدار از برد را دارا است.
\(\begin{array}{*{20}{l}}{D = \mathbb{N}}\\{R = \left\{ {5\:,\:8\:,\:11\:,\:14\:,\:17\:,\:19\:,\: \cdots } \right\}}\end{array}\)

12 نمودار تابعی، یک سهمی است که از نقاط (1, -2) و (2,-3) می گذرد و محور yها را در نقطه ای به عرض ١ قطع می کند. نمایش جبری این تابع را بیابید و نمودار آن را رسم و دامنه و برد تابع را مشخص کنید.
\(\begin{array}{*{20}{l}}\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\\end{array}\\\begin{array}{l}\left( {1{\mkern 1mu} ,{\mkern 1mu} - 2} \right) \Rightarrow - {\mkern 1mu} 2 = a{\left( 1 \right)^2} + b\left( 1 \right) + c \Rightarrow a + b + c = - 2\\\end{array}\\\begin{array}{l}\left( {2{\mkern 1mu} ,{\mkern 1mu} - 1} \right) \Rightarrow - 1 = a{\left( 2 \right)^2} + b\left( 2 \right) + c \Rightarrow 4a + 2b + c = - 1\\\end{array}\\\begin{array}{l}\left( {0{\mkern 1mu} ,{\mkern 1mu} 1} \right) \Rightarrow 1 = a{\left( 0 \right)^2} + b\left( 0 \right) + c \Rightarrow c = 1\\\end{array}\\\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a + b = - 3\\\end{array}\\{4a + 2b = - 2}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = 2\\\end{array}\\{b = - 5}\end{array}} \right.\\\\ \Rightarrow y = 2{x^2} - 5x + 1 \Rightarrow y = 2{\left( {x - \frac{5}{4}} \right)^2} - \frac{{13}}{8}\end{array}\end{array}\)

\(\begin{array}{*{20}{l}}{D = \mathbb{R}}\\{R = \left[ {\left. { - \frac{{13}}{8}\:,\:\infty } \right)} \right.}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















