جواب تمرین صفحه 66 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 84.74Mپاسخ تمرین صفحه 66 هندسه یازدهم
-گام به گام تمرین صفحه 66 درس روابط طولی در مثلث
-تمرین صفحه 66 درس 3
-شما در حال مشاهده جواب تمرین صفحه 66 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 یک درخت کج از نقطه A روی زمین، که در فاصله 15متری از نوک درخت است به زاویه °60 دیده می شود. اگر فاصله A تا پای درخت 20 متر باشد، مطلوب است:
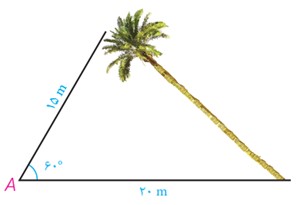
الف طول درخت
ب سینوس زاویه ای که درخت با سطح زمین می سازد.
پ فاصله نوک درخت از زمین
الف
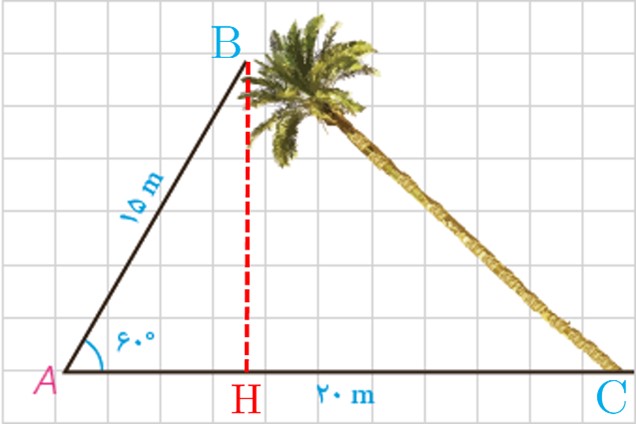
\(\begin{array}{l}{a^2} = {20^2} + {15^2} - 2 \times 20 \times 15 \times \cos {60^ \circ } = 400 + 225 - 300\\ \Rightarrow {a^2} = 325 \Rightarrow a = 5\sqrt {13} \end{array}\)
ب
\(\frac{{5\sqrt {13} }}{{\sin {{60}^ \circ }}} = \frac{{15}}{{\sin C}} \Rightarrow \sin C = \frac{{15 \times \frac{{\sqrt 3 }}{2}}}{{5\sqrt {13} }} \simeq 0/72 \Rightarrow \widehat C \simeq {46^ \circ }\)
پ
\(\sin {60^ \circ } = \frac{{BH}}{{AB}} \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{BH}}{{15}} \Rightarrow BH = \frac{{15\sqrt 3 }}{2}\)
2 در مثلث متساوی الاضلاع ABC به ضلع 8 واحد، نقطه D ، که به فاصله 7 واحد از رأس A قرار دارد از B و C چه فاصله ای دارد؟ (CD>BD) نقطه E ، که به فاصله 5 واحد از C قرار دارد از D به چه فاصله ای است؟ اندازه زاویه AED چند درجه است؟
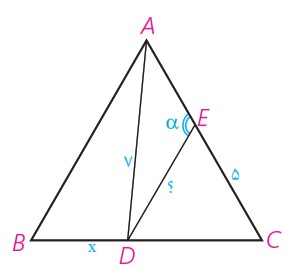
5DC=CE= در نتیجه مثلث DCE متساوی الساقین است و چون یک زاویه 60 درجه دارد، پس متساوی الاضلاع است؛ یعنی 5DE= . در مثلث DCE زاویه α یک زاویه خارجی است؛ پس:
\(\alpha = {60^ \circ } + {60^ \circ } \Rightarrow \alpha = {120^ \circ }\)
3 یک کشتی از یک نقطه با سرعت 60 کیلومتر در ساعت در یک جهت در حرکت است و یک ساعت بعد با °30 انحراف به راست با سرعت 40 کیلومتر در ساعت به حرکت خود ادامه می دهد و یک ساعت و نیم پس از آغاز حرکتش در یک بندرگاه پهلو می گیرد. فاصله بندرگاه از مبدأ حرکت کشتی چند کیلومتر است؟
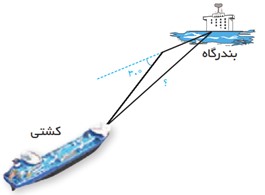
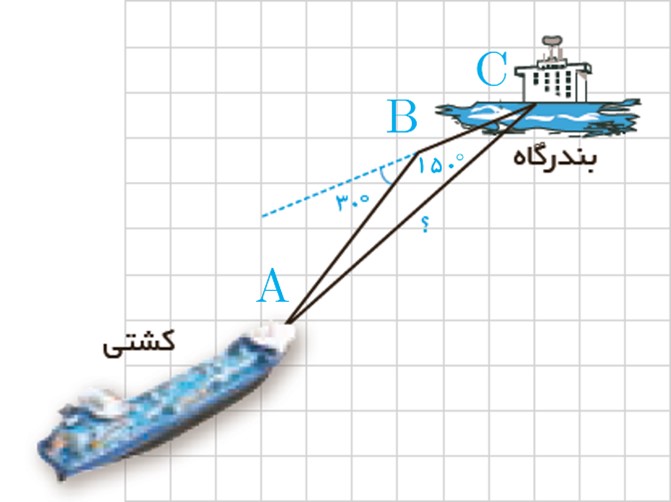
\(\begin{array}{l}AB = 60 \times 1 = 60km\quad ,\quad BC = 40 \times 0/5 = 20km\\\\\\A{C^2} = {60^2} + {20^2} - 2 \times 60 \times 20 \times \cos {150^ \circ } = 3600 + 400 + 1200\sqrt 3 \\\\ \Rightarrow A{C^2} = 400\left( {10 + 3\sqrt 3 } \right)\\\\ \Rightarrow AC = 20\sqrt {10 + 3\sqrt 3 } \end{array}\)
4 در مثلث ABC، میانه AM را رسم کرده ایم \(\left( {MB = MC = \frac{a}{2}} \right)\). با نوشتن قضیه کسینوس ها در دو مثلث AMB و AMC ، \({b^2}\) و \({c^2}\) را محاسبه، و با جمع کردن دو تساوی حاصل، درستی تساوی زیر را ثابت کنید:
(قضیه میانه ها) \({b^2} + {c^2} = 2A{M^2} + \frac{{{a^2}}}{2}\)
در حالت خاص AB=4 و AC=6 و BC=8 ، طول میانه AM را به دست آورید.
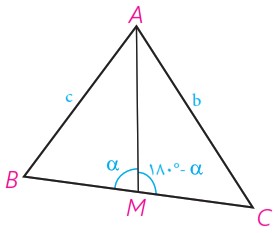
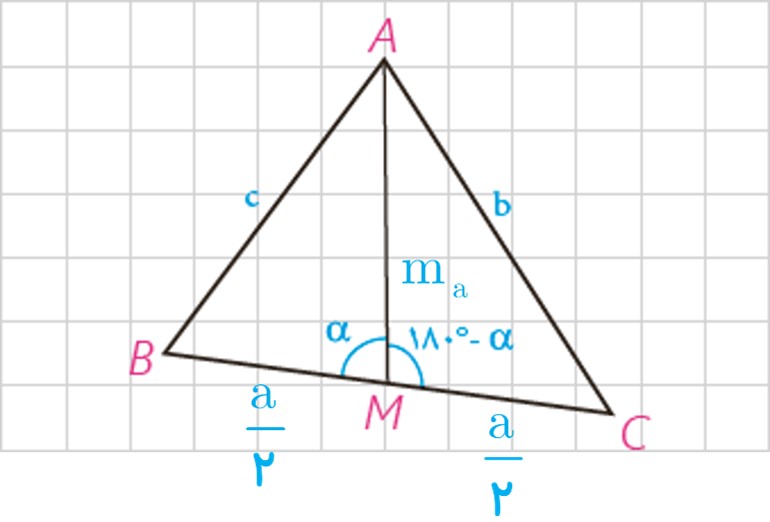
\(\begin{array}{l}A\mathop B\limits^\Delta M:\quad {c^2} = {(\frac{a}{2})^2} + A{M^2} - 2 \times \frac{a}{2} \times AM \times \cos \alpha \\\\{c^2} = \frac{{{a^2}}}{4} + A{M^2} - a \times AM \times \cos \alpha \;\;\;\;\left( 1 \right)\\\\A\mathop C\limits^\Delta M:\quad {b^2} = {(\frac{a}{2})^2} + A{M^2} - 2 \times \frac{a}{2} \times AM \times \cos ({180^ \circ } - \alpha )\\\\{\kern 1pt} {b^2} = \frac{{{a^2}}}{4} + A{M^2} + a \times AM \times \cos \alpha \;\;\;\left( 2 \right)\\\\\mathop \Rightarrow \limits^{\left( 1 \right)\;,\;\left( 2 \right)} \;\;{b^2} + {c^2} = \frac{{{a^2}}}{2} + 2A{M^2}\end{array}\)
\(\begin{array}{l}AB = c = 4\quad ,\quad AC = b = 6\quad ,\quad BC = a = 8\\\\{b^2} + {c^2} = \frac{{{a^2}}}{2} + 2A{M^2}\\\\ \Rightarrow A{M^2} = \frac{{2({b^2} + {c^2}) - {a^2}}}{2} = \frac{{2(36 + 16) - 64}}{2} = 20\\\\ \Rightarrow AM = 2\sqrt 5 \end{array}\)
5 در مثلث ABC ، نقطه دلخواه D روی BC مفروض است. به کمک قضیه کسینوس ها در دو مثلث ADB و ADC درستی تساوی زیر را ثابت کنید:
\(A{B^2}.\;DC + A{C^2}.\;DB = A{D^2}.\;BC + DB\;.\;DC\;.\;BC\)
(قضیه استوارت)
به کمک قضیه استوارت، درستی قضیه میانه ها را نتیجه گیری کنید.
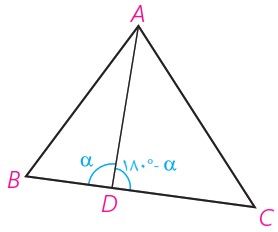
\(\begin{array}{l}A\mathop B\limits^\Delta D:\quad \\\\A{B^2} = A{D^2} + D{B^2} - 2AD \cdot DB \cdot \cos \alpha \end{array}\)
\({\mathop \Rightarrow \limits^{ \times DC} \;\;\;A{B^2} \cdot DC = A{D^2} \cdot DC + D{B^2} \cdot DC - 2DC \cdot AD \cdot DB \cdot \cos \alpha \quad \left( 1 \right)}\)
\(\begin{array}{l}A\mathop C\limits^\Delta D:\quad \\\\A{C^2} = A{D^2} + C{D^2} - 2AD \cdot DC \cdot \cos \left( {{{180}^\circ } - \alpha } \right)\end{array}\)
\({\mathop \Rightarrow \limits^{ \times DB} \;\;A{B^2} \cdot DB = A{D^2} \cdot DB + DB \cdot D{C^2} + 2DB \cdot AD \cdot DC \cdot \cos \alpha \quad \left( 2 \right)}\)
\(\mathop \Rightarrow \limits^{\left( 1 \right) + \left( 2 \right)} \;\;A{B^2} \cdot DC + A{B^2} \cdot DB = A{D^2} \cdot DC + D{B^2} \cdot DC - 2DC \cdot AD \cdot DB \cdot \cos \alpha \)
\({ + A{D^2} \cdot DB + DB \cdot D{C^2} + 2DB \cdot AD \cdot DC \cdot \cos \alpha }\)
\({ \Rightarrow A{B^2} \cdot DC + A{C^2} \cdot DB = A{D^2}\left( {DC + DB} \right) + BD.DC\left( {DC + DB} \right)}\)
\({ \Rightarrow A{B^2} \cdot DC + A{C^2} \cdot DB = A{D^2} \cdot BC + DB \cdot DC \cdot BC}\)
\({DC = DB = \frac{a}{2}\quad ,\quad AC = b\quad ,\quad AB = c}\)
\({\frac{a}{2} \times {c^2} + \frac{a}{2} \times {b^2} = A{D^2} \times a + \frac{a}{2} \times \frac{a}{2} \times a}\)
\({ \Rightarrow \frac{a}{2}({c^2} + {b^2}) = \frac{a}{2}(2A{D^2} + \frac{{{a^2}}}{2})}\)
\({ \Rightarrow {c^2} + {b^2} = 2A{D^2} + \frac{{{a^2}}}{2}}\)
6 مسئله 2 را بار دیگر، این بار به کمک قضیه استوارت حل کنید.
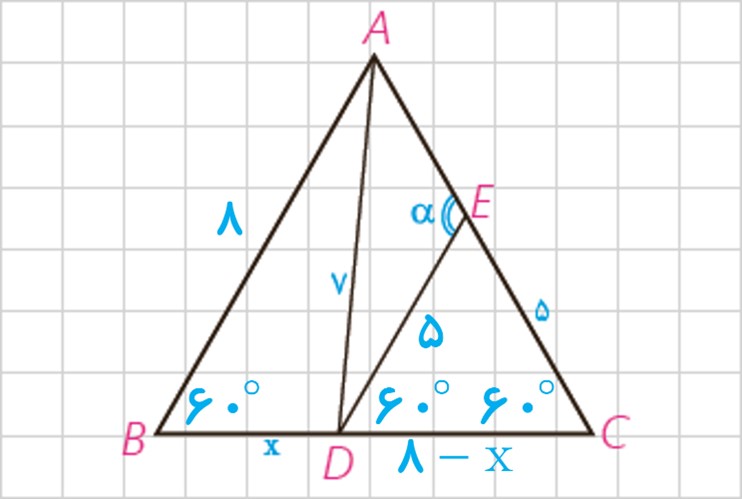
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{AB = AC = BC = 8\;,\;AD = 7\;,\;DB = x}\\\;\\{DC = 8 - x\;,\;DB < DC}\end{array}} \right.}\\{}\\{A{B^2}.DC + A{C^2}.DB = A{D^2}.BC + DB.DC.BC}\\{}\\{ \Rightarrow 64\left( {8 - x} \right) + 64x = 49 \times 8 + 8x\left( {8 - x} \right)}\\{}\\{ \Rightarrow 64 \times 8 - 64x + 64x = 49 \times 8 + 8x\left( {8 - x} \right)}\\{}\\{\mathop \Rightarrow \limits^{ \div 8} \;\;64 = 49 + 8x - {x^2} \Rightarrow {x^2} - 8x + 15 = 0}\\{}\\{ \Rightarrow \left( {x - 3} \right)\left( {x - 5} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{x = 5}\end{array}} \right.}\\{}\\{\mathop \Rightarrow \limits^{DB < DC} \;\;x = DB = 3\quad ,\quad DC = 5}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















