جواب تمرین صفحه 73 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 84.74Mپاسخ تمرین صفحه 73 هندسه یازدهم
-گام به گام تمرین صفحه 73 درس روابط طولی در مثلث
-تمرین صفحه 73 درس 3
-شما در حال مشاهده جواب تمرین صفحه 73 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1
الف در مثلث AC=6 ، AB=10 ، ABC و A=60° ، الف) طول BC را به دست آورید.
ب مساحت مثلث را تعیین کنید.
پ مقدار sinB را پیدا کنید.
الف
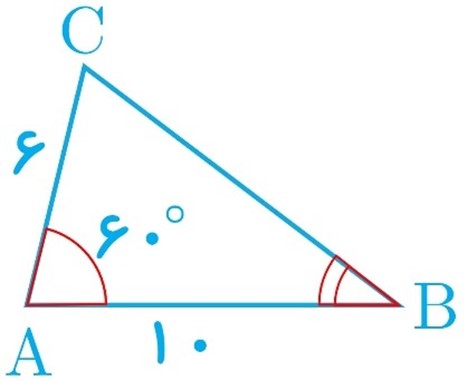
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} - 2AC\,.AB.\cos A\\\\B{C^2} = 36 + 100 - 2 \times 6 \times 10 \times \frac{1}{2} = 76\\\\ \Rightarrow BC = 2\sqrt {19} \end{array}\)
ب
\(S = \frac{1}{2}.AC.AB.\sin A = \frac{1}{2} \times 6 \times 10 \times \frac{{\sqrt 3 }}{2} = 15\sqrt 3 \)
پ
\(\begin{array}{l}\frac{{\sin B}}{b} = \frac{{\sin A}}{a} \Rightarrow \frac{{\sin B}}{6} = \frac{{\frac{{\sqrt 3 }}{2}}}{{2\sqrt {19} }}\\\\ \Rightarrow \sin B = \frac{3}{2}\sqrt {\frac{3}{{19}}} \Rightarrow \sin B = \frac{{3\sqrt {57} }}{{38}}\end{array}\)
2 دو زمین کوچک به شکل مثلث با یک دیوار به طول 13 متر مطابق شکل از هم جدا شده اند. ابعاد زمین ها هم در شکل مشخص شده اند. اگر با برداشتن دیوار، دو زمین به یک زمین تبدیل شود، مساحت آن چقدر می شود؟
نشان دهید دیوار مشترک با اضلاع 4 متری و 11 متری زاویه های برابر می سازد. (\(α=β\))
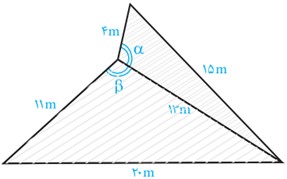
\(\begin{array}{l}{S_{ABCD}} = {S_{ABD}} + {S_{BCD}}\\\\{P_{ABD}} = \frac{{4 + 13 + 15}}{2} = 16\\\\{P_{BCD}} = \frac{{11 + 13 + 20}}{2} = 22\\\\{S_{ABD}} = \sqrt {16 \times 12 \times 3 \times 1} = 24\\\\{S_{BCD}} = \sqrt {22 \times 11 \times 9 \times 2} = 66\\\\{S_{ABCD}} = 24 + 66 = 90\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}{S_{ABD}} = \frac{1}{2}AB.BD.\sin \alpha \\{S_{BCD}} = \frac{1}{2}BC.BD.\sin \beta \end{array} \right\} \Rightarrow \\\\\left. \begin{array}{l}24 = \frac{1}{2} \times 4 \times 13 \times \sin \alpha \\66 = \frac{1}{2} \times 11 \times 13 \times \sin \beta \end{array} \right\} \Rightarrow \\\\\left. \begin{array}{l}\sin \alpha = \frac{{12}}{{13}}\\\sin \beta = \frac{{12}}{{13}}\end{array} \right\} \Rightarrow \sin \alpha = \sin \beta \end{array}\)
3 دستور محاسبه مساحت مثلث متساویالاضلاع به ضلع a را به کمک دستور هرون به دست آورید.
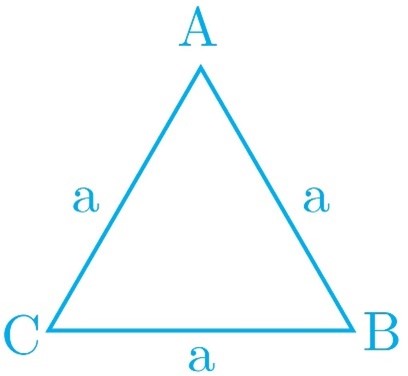
\(\begin{array}{l}AB = AC = BC = a \Rightarrow {P_{ABC}} = \frac{{3a}}{2}\\\\{S_{ABC}} = \sqrt {\frac{{3a}}{2}{{(\frac{{3a}}{2} - a)}^3}} \\\\ = \sqrt {\frac{{3a}}{2}{{(\frac{a}{2})}^3}} = \sqrt {\frac{{3{a^4}}}{{16}}} = \frac{{\sqrt 3 }}{4}{a^2}\end{array}\)
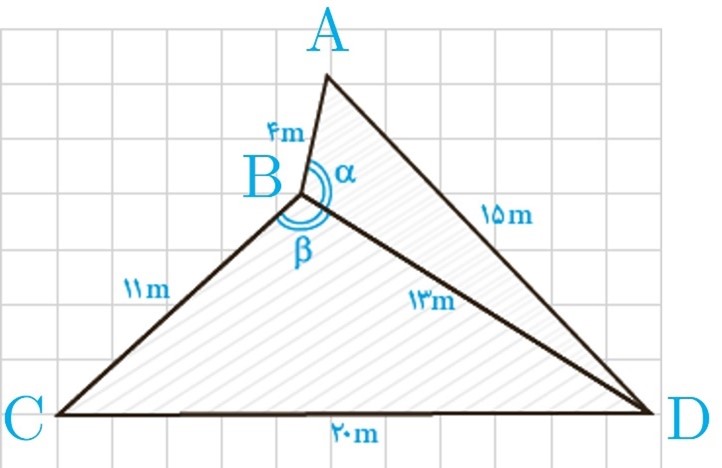
4 در شکل مقابل، اولاً طول BC را به دست آورید. ثانیاً مساحت چهارضلعی DECB را بیابید.
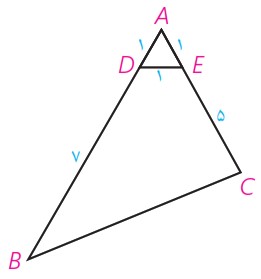
با توجه به اینکه مثلث ADE متساوی الساقین است، پس \(D\hat AE = {60^ \circ }\) در نتیجه:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\\\\B{C^2} = 36 + 64 - 2 \times 6 \times 8 \times \frac{1}{2} = 52\\\\ \Rightarrow BC = 2\sqrt {13} \\\\{S_{BCED}} = {S_{ABC}} - {S_{ADE}}\\\\{S_{ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2} \times 8 \times 6 \times \frac{{\sqrt 3 }}{2}\\ = 12\sqrt 3 \\\\{S_{ADE}} = \frac{{\sqrt 3 }}{4}{a^2} = \frac{{\sqrt 3 }}{4} \times {1^2} = \frac{{\sqrt 3 }}{4}\\\\{S_{BCED}} = 12\sqrt 3 - \frac{{\sqrt 3 }}{4} = \frac{{47\sqrt 3 }}{4}\end{array}\)
5 در شکل صفحه بعد AD نیمساز زاویه A است.
با پر کردن جاهای خالی، دستوری دیگر برای محاسبه طول نیمساز زاویه A به دست آورید.
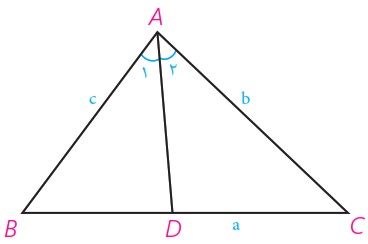
\(\begin{array}{l}{S_{ABC}} = {S_{ABD}} + {S_{ACD}}\; \Rightarrow \\\\\frac{1}{2}AB\;.\;AC\;.\;\sin A = \frac{1}{2}\;....\; \times \;....\; \times \sin \frac{A}{2} + \frac{1}{2}\;....\; \times \;....\; \times \sin \frac{A}{2}\\\\ \Rightarrow \;\;AB\;.\;AC\;.\;\sin A = AD\;.\;\sin \frac{A}{2}\left( {....\; + \;....} \right)\\\\ \Rightarrow \;AD = \frac{{AB\;.\;AC\;.\;\sin A}}{{\left( {....\; + \;....} \right)\sin \frac{A}{2}}} = \frac{{2AB\;.\;AC\;.\;\sin \frac{A}{2}\cos \frac{A}{2}}}{{\left( {....\; + \;....} \right)\sin \frac{A}{2}}}\end{array}\)
\({d_a} = \frac{{2bc\;.\;\cos \frac{A}{2}}}{{b + c}}\) (نیمساز رأس A) \( \Rightarrow \;AD = ....\;\; \Rightarrow \)
\(\begin{array}{l}{S_{ABC}} = {S_{ABD}} + {S_{ACD}}\; \Rightarrow \\\\\frac{1}{2}AB\;.\;AC\;.\;\sin A = \frac{1}{2}AB\; \times AD\; \times \sin \frac{A}{2} + \frac{1}{2}AC \times AD\; \times \sin \frac{A}{2}\\\\ \Rightarrow \;\;AB\;.\;AC\;.\;\sin A = AD\;.\;\sin \frac{A}{2}\left( {AB + AC} \right)\\\\ \Rightarrow \;AD = \frac{{AB\;.\;AC\;.\;\sin A}}{{\left( {AB + AC} \right)\sin \frac{A}{2}}} = \frac{{2AB\;.\;AC\;.\;\sin \frac{A}{2}\cos \frac{A}{2}}}{{\left( {AB + AC} \right)\sin \frac{A}{2}}}\end{array}\)
\({d_a} = \frac{{2bc\;.\;\cos \frac{A}{2}}}{{b + c}}\) (نیمساز رأس A) \( \Rightarrow \;AD = {d_a}\;\; \Rightarrow \)
6 در مثلث ABC به اضلاع 5 و 6 و 7 سانتیمتر، نقطه ای که از اضلاع به طول های 5 و 6، به فاصله 2 و 3 سانتیمتر است از ضلع بزرگتر چه فاصله ای دارد؟
راهنمایی: از مساحت مثلث استفاده کنید.
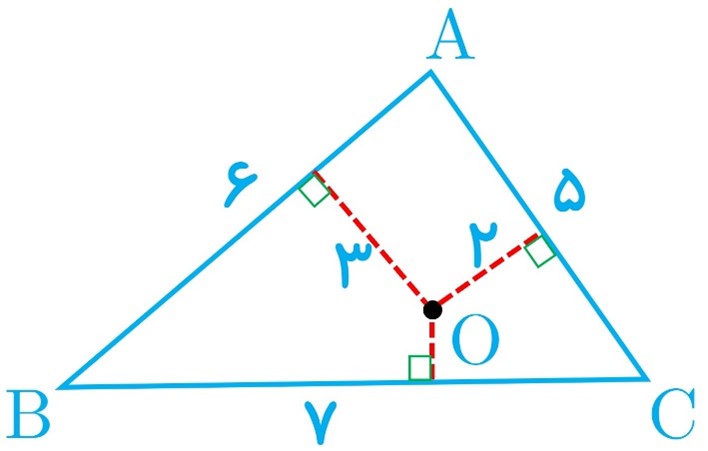
\(\begin{array}{l}{S_{ABC}} = {S_{OAB}} + {S_{OAC}} + {S_{OBC}}\\\\{P_{ABC}} = \frac{{5 + 6 + 7}}{2} = 9\\\\{S_{ABC}} = \sqrt {9 \times 2 \times 3 \times 4} = 6\sqrt 6 \\\\{S_{OAB}} = \frac{1}{2} \times 6 \times 3 = 9\\\\{S_{OAC}} = \frac{1}{2} \times 5 \times 2 = 5\\\\{S_{OBC}} = \frac{1}{2} \times 7 \times x = \frac{7}{2}x\\\\6\sqrt 6 = 9 + 5 + \frac{7}{2}x\\\\ \Rightarrow x = \frac{2}{7}(6\sqrt 6 - 14) \simeq 0/2\end{array}\)
7 در شکل، اولاً اندازه زاویه A را به دست آورید. ثانیاً مساحت چهارضلعی ABCD را بیابید.
راهنمایی: B را به D وصل کنید.
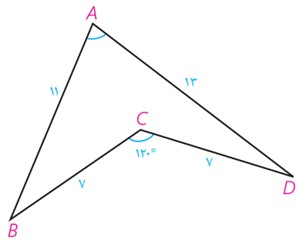
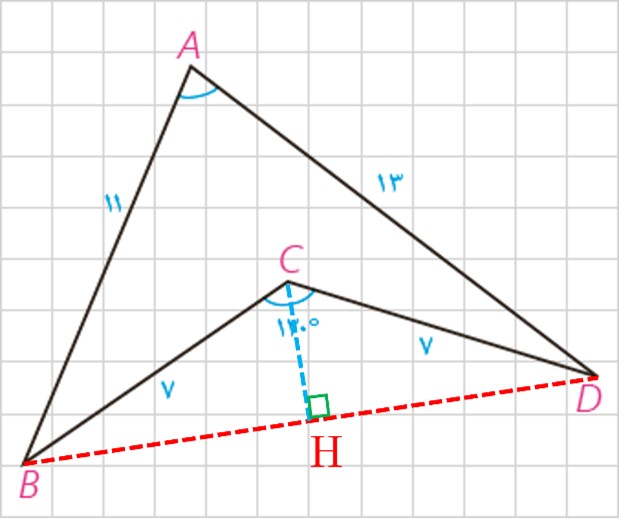
مثلث BCD متساوی الساقین است و با توجه به اندازه زاویه C ، دو زاویه دیگر هر کدام 30 درجه خواهد بود. در مثلث قائم الزاویه CHD \(\widehat {CDH} = {30^ \circ }\)، در نتیجه: \(CH = \frac{7}{2}\)
\(\begin{array}{l}\left. \begin{array}{l}{S_{BCD}} = \frac{1}{2} \times \frac{7}{2} \times BD = \frac{7}{4}BD\\{S_{BCD}} = \frac{1}{2} \times 7 \times 7 \times \sin {120^ \circ } = \frac{{49\sqrt 3 }}{4}\end{array} \right\}\\\\ \Rightarrow \frac{7}{4}BD = \frac{{49\sqrt 3 }}{4} \Rightarrow BD = 7\sqrt 3 \\\\{P_{ABD}} = \frac{{11 + 13 + 7\sqrt 3 }}{2} = 12 + \frac{{7\sqrt 3 }}{2}\\\\{S_{ABD}} = \sqrt {(12 + \frac{{7\sqrt 3 }}{2})(12 + \frac{{7\sqrt 3 }}{2} - 7\sqrt 3 )(12 + \frac{{7\sqrt 3 }}{2} - 11)(12 + \frac{{7\sqrt 3 }}{2} - 13)} \\\\{S_{ABD}} = \sqrt {(12 + \frac{{7\sqrt 3 }}{2})(12 - \frac{{7\sqrt 3 }}{2})(\frac{{7\sqrt 3 }}{2} + 1)(\frac{{7\sqrt 3 }}{2} - 1)} \\\\{S_{ABD}} = \sqrt {(144 - \frac{{174}}{4})(\frac{{147}}{4} - 1)} = \frac{{143}}{4}\sqrt 3 \quad \left( 1 \right)\\\\{S_{ABD}} = \frac{1}{2} \times 11 \times 13 \times \sin A = \frac{{143}}{2}\sin A\quad \left( 2 \right)\\\\\mathop \Rightarrow \limits^{\left( 1 \right)\;,\;\left( 2 \right)} \;\;\frac{{143}}{2}\sin A = \frac{{143}}{4}\sqrt 3 \Rightarrow \sin A = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat A = {60^ \circ }\\\\{S_{ABCD}} = {S_{ABD}} - {S_{BCD}} = \frac{{143}}{4}\sqrt 3 - \frac{{49}}{4}\sqrt 3 = \frac{{47}}{2}\sqrt 3 \\\end{array}\)
8 ثابت کنید مساحت هر متوازی الاضلاع برابر است با حاصلضرب دو ضلع مجاور در سینوس زاویه بین آن دو ضلع.
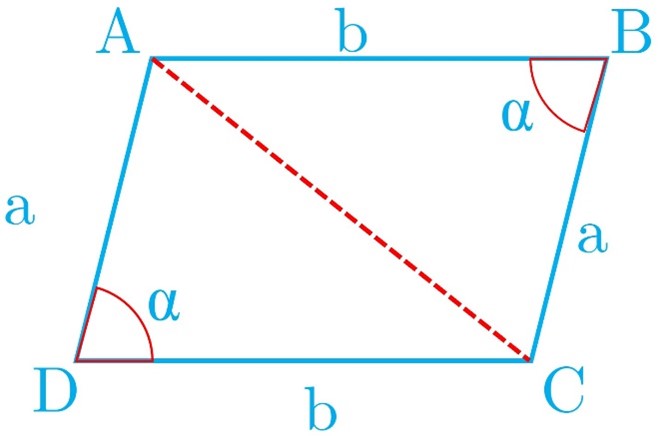
با توجه به خواص متوازی الاضلاع داریم :
\(\begin{array}{l}{S_{ABCD}} = 2\,{S_{ABC}} = 2 \times \frac{1}{2} \times a \times b \times \sin \alpha \\\\ \Rightarrow {S_{ABCD}} = a.b\sin \alpha \end{array}\)
9 به کمک قضیه کسینوس ها ثابت کنید در مثلث ABC :
الف \(A > {90^\circ }\) اگر و تنها اگر a2>b2+c2
ب \(A < {90^\circ }\) اگر و تنها اگر a2<b2+c2
پ \(A = {90^\circ }\) اگر و تنها اگر a2=b2+c2
الف
\(\begin{array}{l}\widehat A > {90^ \circ } \Leftrightarrow \cos A < 0\;\;\mathop \Leftrightarrow \limits_{ \div bc}^{ \times bc} \;bc.\cos A < 0\\\\ \Leftrightarrow - bc.\cos A > 0\;\;\mathop \Leftrightarrow \limits_{ - \left( {{b^2} + {c^2}} \right)}^{ + \left( {{b^2} + {c^2}} \right)} \\\\{b^2} + {c^2} - bc.\cos A > {b^2} + {c^2}\\\\ \Leftrightarrow {a^2} > {b^2} + {c^2}\end{array}\)
ب
\(\begin{array}{l}\widehat A < {90^ \circ } \Leftrightarrow \cos A > 0\;\mathop \Leftrightarrow \limits_{ \div bc}^{ \times bc} bc.\cos A > 0\\\\ \Leftrightarrow - bc.\cos A < 0\;\;\mathop \Leftrightarrow \limits_{ - \left( {{b^2} + {c^2}} \right)}^{ + \left( {{b^2} + {c^2}} \right)} \\\\{b^2} + {c^2} - bc.\cos A < {b^2} + {c^2}\\\\ \Leftrightarrow {a^2} < {b^2} + {c^2}\end{array}\)
پ
\(\begin{array}{l}\widehat A = {90^ \circ } \Leftrightarrow \cos A = 0\;\;\mathop \Leftrightarrow \limits_{ \div bc}^{ \times bc} \;bc.\cos A = 0\\\\ \Leftrightarrow - bc.\cos A = 0\;\;\mathop \Leftrightarrow \limits_{ - \left( {{b^2} + {c^2}} \right)}^{ + \left( {{b^2} + {c^2}} \right)} \\\\{b^2} + {c^2} - bc.\cos A = {b^2} + {c^2}\\\\ \Leftrightarrow {a^2} = {b^2} + {c^2}\end{array}\)
10 به کمک نتیجه تمرین 9، حاده (تند)، قائمه یا منفرجه (باز) بودن زاویه A را در هر یک از مثلث های زیر تعیین کنید:
الف BC = 9 ، AC = 6 ، AB = 10
ب BC = 9 ، AC = 4 ، AB = 8
پ BC = 17 ، AC = 15 ، AB = 8
الف
\(\begin{array}{l}a = 9\quad ,\quad b = 6\quad ,\quad c = 10\\\\{a^2} = 81\quad ,\quad {b^2} + {c^2} = 136\\\\ \Rightarrow {a^2} < {b^2} + {c^2} \Rightarrow \widehat A < {90^ \circ }\end{array}\)
ب
\(\begin{array}{l}a = 9\quad ,\quad b = 4\quad ,\quad c = 8\\\\{a^2} = 81\quad ,\quad {b^2} + {c^2} = 80\\\\ \Rightarrow {a^2} > {b^2} + {c^2} \Rightarrow \widehat A > {90^ \circ }\end{array}\)
پ
\(\begin{array}{l}a = 17\quad ,\quad b = 15\quad ,\quad c = 8\\\\{a^2} = 289\quad ,\quad {b^2} + {c^2} = 289\\\\ \Rightarrow {a^2} = {b^2} + {c^2} \Rightarrow \widehat A = {90^ \circ }\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















