جواب فعّالیت 3 صفحه 61 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 84.75Mپاسخ فعّالیت 3 صفحه 61 هندسه یازدهم
-گام به گام فعّالیت 3 صفحه 61 درس روابط طولی در مثلث
-فعّالیت 3 صفحه 61 درس 3
-شما در حال مشاهده جواب فعّالیت 3 صفحه 61 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
الف مثلث ABC با زاویه های حاده، A و B و C و دایره محیطی آن به مرکز O (که درون مثلث است) را در نظر می گیریم. قطر BD را رسم و D را به A وصل می کنیم.
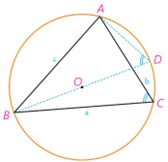
1 زوایای C و D چرا با هم برابرند؟
2 چرا مثلث ABD در رأس A قائم الزاویه است؟
3 با توجه به دو قسمت قبل، داریم:
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} C = {\mathop{\rm Sin}\nolimits} D\;\;,\;\;{\mathop{\rm Sin}\nolimits} D = \frac{{\;...\;}}{{...}}\\\\ \to {\mathop{\rm Sin}\nolimits} C = \frac{{\;...\;}}{{2R}}\; \to \;\frac{C}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
4 به طور مشابه (با وصل کردن A و C به مرکز و رسم قطرهای گذرنده از آن نقاط) خواهیم داشت:
\(\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = ...\;\;,\;\;\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = ...\)
الف
1
این دو زاویه محاطی هستند و هر دو روبه رو به کمان \(AB\) هستند، پس با هم برابرند و هم اندازه اند.
2
زیرا زاویه A محاطی رو به رو به قطر دایره است:
\(\widehat A = \frac{{\mathop {BCD}\limits^\frown \,}}{2} = \frac{{{{180}^ \circ }}}{2} = {90^ \circ }\)
3
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} C = {\mathop{\rm Sin}\nolimits} D\;\;,\;\;{\mathop{\rm Sin}\nolimits} D = \frac{c}{{BD}}\\\\ \to {\mathop{\rm Sin}\nolimits} C = \frac{c}{{2R}}\; \to \;\frac{C}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
4
\(\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R\;\;,\;\;\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R\)
ب حال فرض می کنیم یکی از زوایای مثلث، مثلاً زاویه A، منفرجه باشد \(\left( {\widehat A > {{90}^\circ }} \right)\)، در این صورت O، مرکز دایره محیطی مثلث، بیرون مثلث است و نقطه ʹA را روی کمان BC طوری در نظر می گیریم که O درون مثلث AʹBC بیفتد (یعنی مثلث AʹBC حاده الزوایا باشد.)

1 زوایای A (از مثلث ABC) و زاویه 'A نسبت به هم چگونه اند؟ چرا؟
\(\widehat A + \widehat A' = {180^\circ }\) بنابراین با توجه به آنچه از مثلثات می دانیم، نتیجه می شود:
\(\sin A = \sin \left( {... - \widehat A'} \right) = ...\)
و در مثلث AʹBC مطابق نتیجه قسمت (الف) می توانیم بنویسیم:
\(\frac{a}{{\sin A'}} = ...\; \to \;\frac{a}{{\sin A}} = ...\)
٢ قطر CD را رسم می کنیم، چرا مثلث ADC در رأس A قائم الزاویه است؟ زاویه D در این مثلث، با کدام زاویه از مثلث ABC برابر است؟ چرا؟
٣ با توجه به تعریف نسبت های مثلثاتی در مثلث قائم الزاویه ADC می توان نوشت:
\(\sin D = \frac{{\;...\;}}{{...}} = \frac{b}{{...}}\; \to \;\sin B = \frac{b}{{2R}}\)
و به طریق مشابه (با رسم قطر گذرنده از B) می توان ثابت کرد:
\(\sin C = \frac{c}{{2R}}\)
نتیجه: در هر مثلث دلخواه، نسبت اندازۀ هر ......... به ........ زاویە روبه رو به آن برابر است با .........
ب
1
این دو زاویه مکمل هم هستند:
راه اول:
چهار ضلعی ABA’C محاطی است، پس بنا بر قضیه زوایای مقابل مکمل هستند.
راه دوم:
\(\begin{array}{l}\left. \begin{array}{l}\widehat A = \frac{{\widehat {BA'C}}}{2}\\\widehat {A'} = \frac{{\widehat {BAC}}}{2}\end{array} \right\}\\\\ \Rightarrow \widehat A + \widehat {A'} = \frac{{\widehat {BA'C}}}{2} + \frac{{\widehat {BAC}}}{2}\\\\ = \frac{{\widehat {BA'C} + \widehat {BAC}}}{2} = \frac{{{{360}^ \circ }}}{2} = {180^ \circ }\\\\\sin A = \sin \left( {180^\circ - \widehat A'} \right) = \sin A'\\\\\frac{a}{{\sin A'}} = 2R \to \;\frac{a}{{\sin A}} = 2R\end{array}\)
2
به این دلیل که وتر CD از مرکز دایره می گذرد و بنابراین قطر دایره می باشد و همچنین زاویه ظلی CAD رو به کمان CD می باشد. همانطور که می دانیم کمان CD برابر با 180 درجه می باشد؛ در نتیجه زاویه CAD برابر با نصف کمان CD و برابر با 90 درجه می شود. در نتیجه مثلث ADC در رأس A قائم الزاویه می باشد.
\(\begin{array}{l}\mathop {CD}\limits^\frown {\mkern 1mu} = {180^ \circ }\\\\ \Rightarrow C\hat AD = \frac{{\mathop {CD}\limits^\frown {\mkern 1mu} }}{2} = \frac{{\mathop {{{180}^ \circ }}\limits^\frown {\mkern 1mu} }}{2} = {90^ \circ }\end{array}\)
همچنین زاویه D چون رو به کمان AC می باشد، با زاویه B برابر می باشد:
\(\left\{ \begin{array}{l}\hat D = \frac{{\mathop {AC}\limits^\frown }}{2}{\mkern 1mu} \\\\\hat B = \frac{{\mathop {AC}\limits^\frown }}{2}{\mkern 1mu} \end{array} \right. \Rightarrow \hat D = \hat B\)
3
\(\sin D = \frac{{AC}}{{DC}} = \frac{b}{{2R}}\; \to \;\sin B = \frac{b}{{2R}}\)
نتیجه: در هر مثلث دلخواه، نسبت اندازۀ هر ...ضلع... به ...سینوس... زاویە روبه رو به آن برابر است با ...طول قطر دایره محاطی مثلث...
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















