1736019749.png)
جواب سؤال متن صفحه 69 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 78.81Mپاسخ سؤال متن صفحه 69 هندسه یازدهم
-گام به گام سؤال متن صفحه 69 درس روابط طولی در مثلث
-سؤال متن صفحه 69 درس 3
-شما در حال مشاهده جواب سؤال متن صفحه 69 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
در مثلث ABC برای محاسبهٔ طول نیمساز داخلی زاویهٔ \(({\hat A_1} = {\hat A_2})\,\,\hat A\)، یعنی AD ، AD را امتداد می دهیم تا دایرهٔ محیطی مثلث را در E قطع کند و E را به C وصل می کنیم.
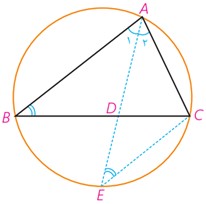
الف چرا \(\,\hat E = \hat B\)؟
ب چرا مثلث های ABD و AEC متشابه اند؟
پ نسبت های اضلاع متناظر آن ها را بنویسید.
\(\frac{{AC}}{ \cdots } = \frac{{AE}}{ \cdots } = \frac{ \cdots }{{BD}}\)
ث از تناسب اول نتیجه می گیریم:
\(\begin{array}{l}AB.AC = AD.AE = AD(AD + DE) = \\\\A{D^2} + AD.DE\end{array}\)
و چون AD.DE=BD.DC (چرا؟) بنابراین:
\(A{D^2} = AB.AC - AD.DE\)
الف
زیرا این دو زاویه هر دو محاطی هستند و رو به رو به یک کمان (کمان AC) هستند.
ب
\(A\mathop B\limits^\Delta C \sim A\mathop E\limits^\Delta C\) طبق قضیه اول تشابه \(\left\{ \begin{array}{l}{{\hat A}_1} = {{\hat A}_2}\\\\\hat B = \hat E\end{array} \right. \Rightarrow \)
پ
\(\frac{{AC}}{{AD}} = \frac{{AE}}{{AB}} = \frac{{CE}}{{BD}}\)
ت
دو وتر AE و BC یکدیگر را در نقطه D درون دایره قطع کرده اند. بنابر قضیه ای داریم:
\(AD . DE = DB . DC\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
