آیا تمام سوالات فعّالیت 2 صفحه 61 هندسه یازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعّالیت 2 صفحه 61 هندسه یازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعّالیت 2 صفحه 61 درس 3 هندسه یازدهم (روابط طولی در مثلث)

تعداد بازدید : 78.81M

پاسخ فعّالیت 2 صفحه 61 هندسه یازدهم

گام به گام فعّالیت 2 صفحه 61 درس روابط طولی در مثلث

فعّالیت 2 صفحه 61 درس 3

شما در حال مشاهده جواب فعّالیت 2 صفحه 61 هندسه یازدهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

الف در کتاب هندسه 1 دیدیم که عمودمنصف های اضلاع هر مثلث در یک نقطه همرس اند و در این کتاب دیدیم که این نقطه، مرکز دایره محیطی مثلث است. دایره محیطی مثلث قائم الزاویه ABC را رسم می کنیم. مرکز این دایره، کجاست و چرا قطر آن با وتر مثلث برابر است؟

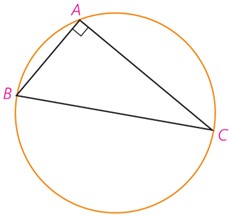
ب با توجه به نتیجه فعالیت (1) می توانیم بگوییم:

در هر مثلث قائم الزاویه، نسبت اندازۀ هر ضلع به سینوس زاویۀ روبه رو به آن ضلع برابر است با اندازۀ ............ دایرۀ محیطی مثلث.

اکنون نشان می دهیم این نتیجه گیری برای هر مثلث دلخواه نیز درست است.

الف

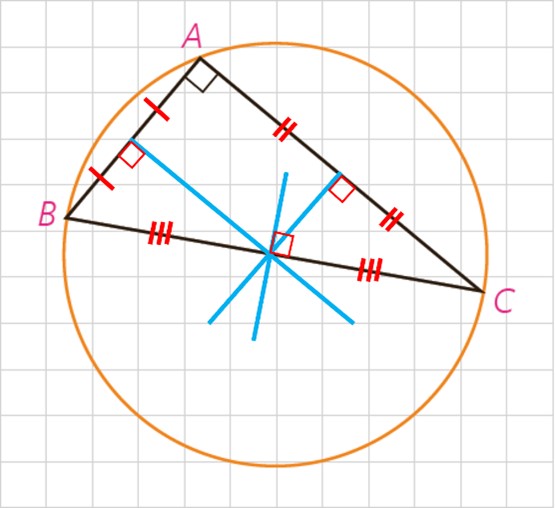
محل برخورد عمود منصف ها در هر مثلث قائم الزاویه، وسط وتر است. پس مرکز این دایره وسط وتر است. \(\widehat {BAC} = {90^ \circ }\) یک زاویه محاطی است و اندازه کمان مقابل آن 180° است یعنی وتر BC دایره را به دو قسمت مساوی تقسیم می کند، یعنی قطر دایره است.

قطر