1736019749.png)
جواب تمرین صفحه 70 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 78.81Mپاسخ تمرین صفحه 70 هندسه یازدهم
-گام به گام تمرین صفحه 70 درس روابط طولی در مثلث
-تمرین صفحه 70 درس 3
-شما در حال مشاهده جواب تمرین صفحه 70 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 در مثلث M ،ABC وسط BC و MP و MQ نیمسازهای زوایای AMC و AMB هستند؛ ثابت کنید: PQ||BC
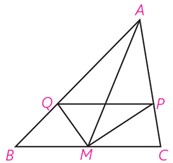
در مثلث AMB پاره خط MQ نیمساز زاویه AMB و در مثلث AMC پاره خط MP نیمساز زاویه AMC است. پس داریم:
\(\left. \begin{array}{l}\frac{{AM}}{{MB}} = \frac{{AQ}}{{QB}}\;\;\mathop \Rightarrow \limits^{MB = MC} \;\;\frac{{AM}}{{MC}} = \frac{{AQ}}{{QB}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{AM}}{{MC}} = \frac{{AP}}{{PB}}\end{array} \right\} \Rightarrow \frac{{AQ}}{{QB}} = \frac{{AP}}{{PB}}\)
\(PQ\parallel BC\) عکس قضیه تالس
2 در مثلث AB=7 ، ABC و AC=4 و BC=10 است. طول نیمساز زاویه داخلی C را به دست آورید.
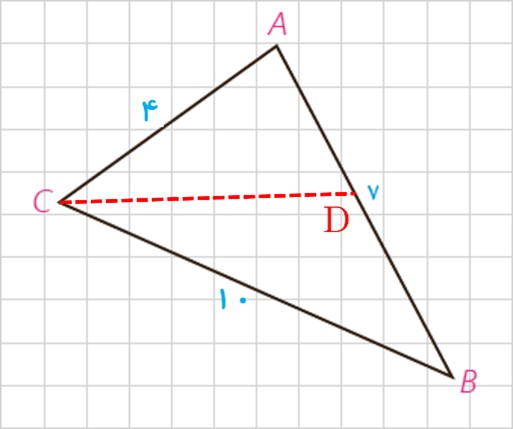
\(\begin{array}{l}C{D^2} = AC.BC - AD\,.BD\\\\\frac{{BC}}{{AC}} = \frac{{BD}}{{DA}} \Rightarrow \frac{{10}}{4} = \frac{{BD}}{{DA}}\\\\ \Rightarrow \frac{{10 + 4}}{4} = \frac{{BD + DA}}{{DA}} \Rightarrow \frac{{14}}{4} = \frac{7}{{DA}}\\\\ \Rightarrow DA = \frac{{28}}{{14}} = 2 \Rightarrow BD = 7 - 2 = 5\\\\C{D^2} = 4 \times 10 - 2 \times 5 = 30 \Rightarrow CD = \sqrt {30} \end{array}\)
3 با پر کردن جاهای خالی با فرض اینکه در شکل مقابل AD نیمساز زاویه A است، روش دیگری برای اثبات قضیه نیمسازهای زوایای داخلی ارائه کنید:
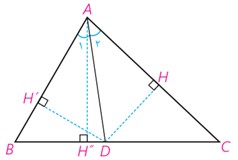
الف چرا 'DH = DH ؟
\(\frac{{{S_{ABD}}}}{{{S_{ACD}}}} = \frac{{\frac{1}{2}DH'\; \times ....\;}}{{\frac{1}{2}DH\; \times ....\;}} = \frac{{\;....\;}}{{....}}\;\;(1)\)
ب
\(\frac{{{S_{ABD}}}}{{{S_{ACD}}}} = \frac{{\frac{1}{2}BD\; \times ....\;}}{{\frac{1}{2}CD\; \times ....\;}} = \frac{{\;....\;}}{{....}}\;\;(2)\)
از مقایسه (1) و (2) نتیجه می شود: \(\frac{{\;....\;}}{{....}} = \frac{{\;....\;}}{{....}}\)
الف
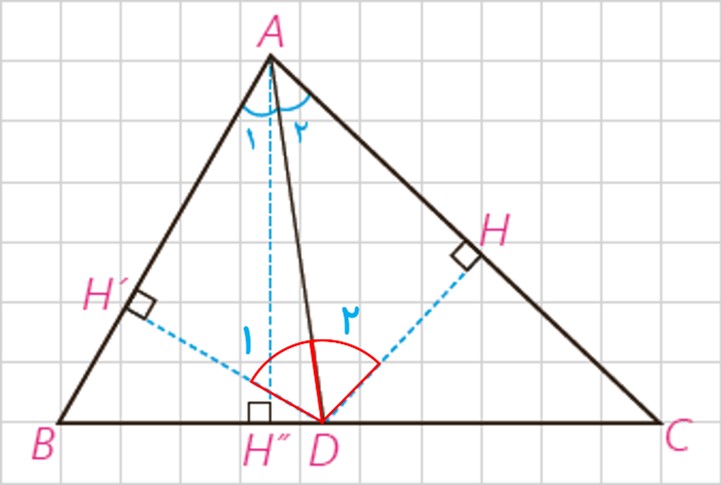
\(\frac{{{S_{ABD}}}}{{{S_{ACD}}}} = \frac{{\frac{1}{2}DH'\; \times AB}}{{\frac{1}{2}DH\; \times AC\;}} = \frac{{AB}}{{AC}}\;\;(1)\)
ب
\(\frac{{{S_{ABD}}}}{{{S_{ACD}}}} = \frac{{\frac{1}{2}BD\; \times AH''}}{{\frac{1}{2}CD\; \times .AH''\;}} = \frac{{BD}}{{CD}}\;\;(2)\)
از مقایسه (1) و (2) نتیجه می شود: \(\frac{{AB}}{{AC}} = \frac{{BD}}{{CD}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
