جواب تمرین صفحه 29 درس 1 ریاضیات گسسته (آشنایی با نظریۀ اعداد)

به دسته هم نهشتی  \({\left[ 3 \right]_{\;9}} = \left\{ {x \in \mathbb{Z}|x = 9k + 3} \right\}\)  تعلق دارد  \(1398\mathop \equiv \limits^9 1 + 3 + 9 + 8\mathop \equiv \limits^9 3 \Rightarrow \)

باقیمانده تقسیم هر عدد صحیح همچون k بر عدد 3 ، یکی از اعداد 0 یا 1 یا 2 می باشد، به عبارت دیگر \(3|k - 0\) یا \(3|k - 1\) یا \(3|k - 2\) وطبق تعریف هم نهشتی \(k\mathop \equiv \limits^3 0\) یا \(k\mathop \equiv \limits^3 1\) یا \(k\mathop \equiv \limits^3 2\) 

\(\begin{array}{l}a\mathop \equiv \limits^m b \Rightarrow a - b\mathop \equiv \limits^m 0 \Rightarrow m|a - b\quad \\\\\mathop \Rightarrow \limits^{n|m} \quad n|a - b \Rightarrow a - b\mathop \equiv \limits^n 0 \Rightarrow a\mathop \equiv \limits^n b\end{array}\)

\(\left. \begin{array}{l}a\mathop \equiv \limits^m b\quad \mathop \Rightarrow \limits^{d|m} \quad a\mathop \equiv \limits^d b\\b\mathop \equiv \limits^m c\quad \mathop \Rightarrow \limits^{d|n} \quad b\mathop \equiv \limits^d c\end{array} \right\} \Rightarrow a\mathop \equiv \limits^d c\)

روش اول : گیریم باقیمانده تقسیم دو عدد بر m برابر 2 باشد، در نتیجه:

\(\left. \begin{array}{l}a\mathop \equiv \limits^m r\\b\mathop \equiv \limits^m r\end{array} \right\} \Rightarrow a\mathop \equiv \limits^m b\)

روش دوم:

\(\begin{array}{l}\left. \begin{array}{l}a = mq + r\\b = mq' + r\end{array} \right\} \Rightarrow a - b = m(q - q')\\\\ \Rightarrow m|a - b \Rightarrow a\mathop \equiv \limits^m b\end{array}\)

اگر \(a\mathop \equiv \limits^m b\) آنگاه باقیمانده تقسیم دو عدد بر a و b بر m ، مساوی است.

اثبات:

گیریم باقیمانده تقسیم a بر  m برابر \({r_1}\) و باقیمانده تقسیم b بر m ، برابر \({r_2}\) باشد، پس:

\(\begin{array}{l}\left. \begin{array}{l}a = mq + {r_1}\\b = mq' + {r_2}\end{array} \right\}\\\\ \Rightarrow a - b = m(q - q') + ({r_1} - {r_2})\quad \left( I \right)\\\\a\mathop \equiv \limits^m b \Rightarrow a - b = mq''\quad \left( {II} \right)\\\\\left. \begin{array}{l}\mathop \Rightarrow \limits^{\left( I \right)\;,\;\left( {II} \right)} \;\;mq'' = m(q - q') + ({r_1} - {r_2})\\\\ \Rightarrow ({r_1} - {r_2}) = m(q'' + q' - q) \Rightarrow m|{r_1} - {r_2}\\\\0 \le {r_1}\;,\;{r_2} < m \Rightarrow \left| {{r_1} - {r_2}} \right| < m\end{array} \right\}\\\\ \Rightarrow \quad \left( {III} \right)\\\\\mathop \Rightarrow \limits^{\left( {III} \right)} {r_1} - {r_2} = 0 \Rightarrow {r_1} = {r_2}\end{array}\)

\(\left. \begin{array}{l}\left( {\begin{array}{*{20}{c}}n\\0\end{array}} \right){a^n} = {a^n}\mathop \equiv \limits^{ab} {a^n}\\\left( {\begin{array}{*{20}{c}}n\\1\end{array}} \right){a^{n - 1}}b\mathop \equiv \limits^{ab} 0\\\left( {\begin{array}{*{20}{c}}n\\2\end{array}} \right){a^{n - 2}}{b^2}\mathop \equiv \limits^{ab} 0\\\left( {\begin{array}{*{20}{c}}n\\3\end{array}} \right){a^{n - 3}}{b^3}\mathop \equiv \limits^{ab} 0\\\;\;\, \vdots \\\left( {\begin{array}{*{20}{c}}n\\{n - 1}\end{array}} \right)a{b^{n - 1}}\mathop \equiv \limits^{ab} 0\\\left( {\begin{array}{*{20}{c}}n\\n\end{array}} \right){b^n} = {b^n}\mathop \equiv \limits^{ab} {b^n}\end{array} \right\}\mathop \Rightarrow \limits^ + \;{(a + b)^n}\mathop \equiv \limits^{ab} {a^n} + {b^n}\)

طبق تمرین 7، می توان نوشت:

\(\begin{array}{l}{(23)^{51}} = {(11 + 12)^{51}}\mathop \equiv \limits^{11 \times 12} {11^{51}} + {12^{51}}\\\\ \Rightarrow {(23)^{51}} - ({11^{51}} + {12^{51}})\mathop \equiv \limits^{132} 0\\\\ \Rightarrow {23^{51}} - {11^{51}} - {12^{51}}\mathop \equiv \limits^{132} 0\end{array}\)

عدد \({23^{51}} - {11^{51}} - {12^{51}}\) بر 132 بخش پذیر است.

\(\begin{array}{l}{2^5}\mathop \equiv \limits^{23} 9\mathop \to \limits^{{{()}^2}} {2^{10}}\mathop \equiv \limits^{23} 81\mathop \equiv \limits^{23} 12\\\\\mathop \to \limits^{ \times 2} {2^{11}}\mathop \equiv \limits^{23} 24\mathop \equiv \limits^{23} 1\mathop \to \limits^{ + 7} {2^{11}} + 7\mathop \equiv \limits^{23} 8\\\\\mathop \to \limits^{ \times 9} ({2^{11}} + 7) \times 9\mathop \equiv \limits^{23} 72\mathop \equiv \limits^{23} 3 \Rightarrow r = 3\end{array}\)

طبق تمرین 5، دو عدد 3a-5 و 4a-7  به پیمانه 10، با یکدیگر هم نهشت اند:

\(\begin{array}{l}4a - 7\mathop { \equiv \;}\limits^{10} 3a - 5 \Rightarrow 4a - 3a\mathop \equiv \limits^{10} \;7 - 5\\\\ \Rightarrow a\mathop \equiv \limits^{10} \;2\;\;\mathop \Rightarrow \limits^{ \times 9} \;\;9\;a\mathop \equiv \limits^{10} 18\\\\\mathop \Rightarrow \limits^{ + 6} \;\;9a + 6\mathop \equiv \limits^{10} 24\mathop \equiv \limits^{10} \;4 \Rightarrow 9a + 6\mathop \equiv \limits^{10} 4\end{array}\)

رقم یکان 4 است.

\(\begin{array}{l}\left. \begin{array}{l}1!\;\mathop \equiv \limits^{10} \;1\\2!\;\mathop \equiv \limits^{10} \;2\\3!\;\mathop \equiv \limits^{10} \;6\\4!\;\mathop \equiv \limits^{10} \;24\;\mathop \equiv \limits^{10} \;4\\5!\;\mathop \equiv \limits^{10} \;20\;\mathop \equiv \limits^{10} \;0\\6!\;\mathop \equiv \limits^{10} \;0\\\;\;\;\; \vdots \\500!\;\mathop \equiv \limits^{10} \;0\end{array} \right\}\\\\\mathop \Rightarrow \limits^ + A\;\mathop \equiv \limits^{10} \;1 + 2 + 6 + 4 + 0 + \cdots + 0 = 13\;\mathop \equiv \limits^{10} \;3\\\\ \Rightarrow A\;\mathop \equiv \limits^{10} \;3\end{array}\)

\(\begin{array}{l}7x + 5y = 11 \Rightarrow 7x = - 5y + 11\\\\ \Rightarrow 7x\;\mathop \equiv \limits^5 \;11 \Rightarrow 7x\;\mathop \equiv \limits^5 \;11 + 2 \times 5 = 21\;\\\\\;\mathop \Rightarrow \limits^{ \div 7} \;x\;\mathop \equiv \limits^5 \;3\;\; \Rightarrow x = 5k + 3\;,\;k \in \mathbb{Z}\quad \\\\\mathop \Rightarrow \limits^{7x + 5y = 11} \;\;\,7(5k + 3) + 5y = 11\\\\ \Rightarrow y = - 7k - 2\;\;,\;\;k \in \mathbb{Z}\end{array}\)

تعداد اسکناس های 2000 تومانی را x و تعداد اسکناس های 5000 تومانی را y در نظر می گیریم؛ بنابراین:

\(\begin{array}{*{20}{l}}{2000x + 5000y = 29000\:\:}\\{}\\{\mathop \Rightarrow \limits^{ \div 1000} \:\:2x + 5y = 29}\\{}\\{5y\:\mathop \equiv \limits^2 \:29 \Rightarrow 5y\:\mathop \equiv \limits^2 \:29 - 12 \times 2 = 5}\\{}\\{\mathop \Rightarrow \limits^{ \div 5} \:\:y\:\mathop \equiv \limits^2 \:1 \Rightarrow y = 2k + 1}\\{}\\{\mathop \Rightarrow \limits^{2x + 5y = 29} \:\:\:2x + 5(2k + 1) = 29}\\{}\\{ \Rightarrow x = - 5k + 12}\end{array}\)

به 3 طریق می توان خرد کرد.

الف

\(\begin{array}{*{20}{l}}\begin{array}{l}\left. {\begin{array}{*{20}{l}}{423\:\mathop \equiv \limits^{11} \:5 \Rightarrow 423x\:\mathop \equiv \limits^{11} \:5x}\\{79\:\mathop \equiv \limits^{11} \:2}\end{array}} \right\}\\\\ \Rightarrow 5x\:\mathop \equiv \limits^{11} \:2 \Rightarrow 5x\:\mathop \equiv \limits^{11} \:2 + 3 \times 11 = 35\end{array}\\\begin{array}{l}\\x\:\mathop \equiv \limits^{11} \:7 \Rightarrow x = 11k + 7\;\;\:,\;\;\:k \in \mathbb{Z}\end{array}\end{array}\)

ب

\(\begin{array}{l}8x\:\mathop \equiv \limits^{12} \:20 - 12 = 8 \Rightarrow x\:\mathop \equiv \limits^3 \:1\\\\ \Rightarrow x = 3k + 1\;\;\:,\;\;\:k \in \mathbb{Z}\end{array}\)

ج

\(\left. {\begin{array}{*{20}{l}}{(51\:,\:6) = 3}\\{3\not{|}11}\end{array}} \right\} \Rightarrow \)

معادله جواب ندارد.

= اسفند + بهمن + دی + آذر + آبان + مهر

\((30 - 1) + 4 \times 30 + 7\: = 156\mathop \equiv \limits^7 \:2\)

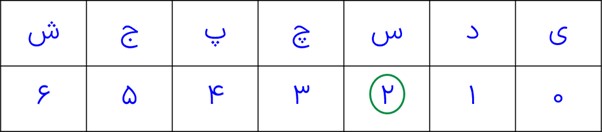
7 اسفند روز سه شنبه می باشد.

= بهمن + دی + آذر + آبان + مهر + شهریور

\( = 31 + 4 \times 30 + 12 = 163\:\mathop \equiv \limits^7 \:2\)

در جدول برای روز جمعه عدد 2 را می نویسیم، سپس اعداد قبل و بعد آن را تعیین می کنیم؛ عدد صفر مربوط به روز 31 مرداد است.

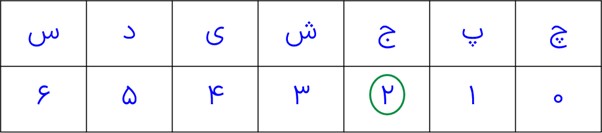
31 مرداد روز چهارشنبه بوده است.

\(\begin{array}{l}5a + 9\;\mathop \equiv \limits^{11} \;0 \Rightarrow 5a\;\mathop \equiv \limits^{11} \; - 9\;\mathop \equiv \limits^{11} \; - 9 + 4 \times 11 = 35\\\\\mathop \to \limits^{ \div 5} a\;\mathop \equiv \limits^{11} \;7 \Rightarrow a = 11k + 7\quad ,\quad k \in \mathbb{Z}\end{array}\)

تعداد وزنه های 3 کیلویی را با x و تعداد وزن های 5 کیلویی را با y نمایش می دهیم؛ بنابراین:

\(\begin{array}{l}3x + 5y = 23 \Rightarrow 5y\;\mathop \equiv \limits^3 \;23\;\mathop \equiv \limits^3 \;23 - 3 = 20\\\\ \Rightarrow y\;\mathop \equiv \limits^3 \;4 \Rightarrow y = 3k + 4\\\\{\mathop \to \limits^{3x + 5y = 23} _{}}3x + 5(3k + 4) = 23 \Rightarrow x = - 5k + 1\end{array}\)

به 2 طریق می توان وزن کرد.

تعداد گل های نوع اول را x و تعداد گل های نوع دوم را  y می نامیم؛ بنابراین:

\(\begin{array}{l}x + y = 9 \Rightarrow x = - y + 9 \Rightarrow x\;\mathop \equiv \limits^1 \;9\\\\ \Rightarrow x = k + 9\;\;\mathop \Rightarrow \limits^{x + y = 9} \;\;k + 9 + y = 9\\\\ \Rightarrow y = - \;k\end{array}\)

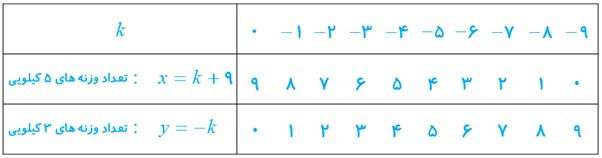
به 10 طریق می توان یک دسته گل شامل 9 شاخه تهیه کرد.

تعداد سؤالات 7 امتیازی گه امتیاز کامل گرفته را با x و تعداد سؤالات 9 امتیازی را که امتیاز کامل گرفته را با y  نمایش می دهیم؛ بنابراین:

\(\begin{array}{l}7x + 9y = 73 \Rightarrow 9y\;\mathop \equiv \limits^7 \;73\;\mathop \equiv \limits^7 \;3\\\\\mathop \Rightarrow \limits^{ \div 3} \;\;3y\;\mathop \equiv \limits^7 \;1\;\mathop \equiv \limits^7 \;1 - 7 = - 6\\\\\mathop \Rightarrow \limits^{ \div 3} \;\;y\;\mathop \equiv \limits^7 \; - 2 \Rightarrow y = 7k - 2\\\\\mathop \Rightarrow \limits^{7x + 9y = 73} \;\;7x + 9(7k - 2) = 73\\\\ \Rightarrow x = - 9k + 13\end{array}\)

\(k = 1 \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 5\end{array} \right. \Rightarrow \)

فقط به یک صورت می توانسته این امتیاز را کسب کند.