جواب تمرین صفحه 8 درس 1 ریاضیات گسسته (آشنایی با نظریۀ اعداد)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 8 ریاضیات گسسته
-گام به گام تمرین صفحه 8 درس آشنایی با نظریۀ اعداد
-تمرین صفحه 8 درس 1
-شما در حال مشاهده جواب تمرین صفحه 8 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 گزاره های زیر را به روش بازگشتی (گزاره های هم ارز) ثابت کنید:
الف اگر x و y دو عدد حقیقی هم علامت باشند داریم:
\(\frac{x}{y} + \frac{y}{x} \ge 2\)
ب برای هر سه عدد حقیقی x و y و z داریم:
\({x^2} + {y^2} + {z^2} \ge xy + yz + zx\)
پ برای هر دو عدد حقیقی x و y داریم:
\({x^2} + {y^2} + 1 \ge xy + x + y\)
الف
اگر x و y دو عدد حقیقی هم علامت (مخالف صفر) باشند، داریم :
\(\begin{array}{l}\frac{x}{y} + \frac{y}{x} \ge 2 \Leftrightarrow xy\;(\frac{x}{y} + \frac{y}{x}) \ge 2xy\\\\ \Leftrightarrow {x^2} + {y^2} \ge 2xy \Leftrightarrow {x^2} + {y^2} - 2xy \ge 0\\\\ \Leftrightarrow {(x - y)^2} \ge 0\end{array}\)
که این عبارت همواره درست است.
ب
برای هر سه عدد حقیقی x و y و z داریم:
\(\begin{array}{l}{x^2} + {y^2} + {z^2} \ge xy + yz + zx\quad \mathop \Leftrightarrow \limits^{ \times 2} \quad \\\\2{x^2} + 2{y^2} + 2{z^2} \ge 2xy + 2yz + 2zx\\\\ \Leftrightarrow \underline {{x^2}} + \underline{\underline {{x^2}}} + \underline {{y^2}} + \underline {\underline{\underline {{y^2}}} } + \underline{\underline {{z^2}}} + \underline {\underline{\underline {{z^2}}} } - \underline {2xy} - \underline {\underline{\underline {2yz}} } - \underline{\underline {2zx}} \ge 0\\\\ \Leftrightarrow {(x - y)^2} + {(x - z)^2} + {(y - z)^2} \ge 0\end{array}\)
که این عبارت همواره درست است.
پ
برای هر سه عدد حقیقی x و y و z داریم:
\(\begin{array}{l}{x^2} + {y^2} + 1 \ge xy + x + y\quad \mathop \Leftrightarrow \limits^{ \times 2} \quad \\\\2{x^2} + 2{y^2} + 2 \ge 2xy + 2x + 2y\\\\ \Leftrightarrow \underline {{x^2}} + \underline{\underline {{x^2}}} + \underline {{y^2}} + \underline {\underline{\underline {{y^2}}} } + \underline{\underline 1} + \underline {\underline{\underline 1} } - \underline {2xy} - \underline{\underline {2x}} - \underline {\underline{\underline {2y}} } \ge 0\\\\ \Leftrightarrow {(x - y)^2} + {(x - 1)^2} + {(y - 1)^2} \ge 0\end{array}\)
که این عبارت همواره درست است.
2 عددی حقیقی مانند x ارائه کنید به طوری که \({x^3} < {x^2}\)
\(x = 0/1\quad ,\quad x = - 1\quad ,\quad x = - 2\quad ,\quad \cdots \)
3 اگر α و \(\beta \) دو عدد گنگ باشند ولی \(\alpha + \exists \) گویا باشد، ثابت کنید \(\alpha - \beta \) و \(\alpha + 2\beta \) گنگ هستند.
(I) گیریم \(\alpha - \beta \) گویا باشد، از طرفی \(\alpha + \beta \) گویاست، پس مجموع آن ها یعنی \(\alpha + \beta + \alpha - \beta = 2\alpha \) گویا بوده و در نتیجه \(\alpha\) نیز گویاست که با فرض، تناقض دارد؛ پس \(\alpha - \beta \) گنگ است.
(II) گیریم \(\alpha + 2\beta \) گویا باشد، از طرفی \(\alpha + \beta \) گویاست، پس تفاضل آن ها یعنی \(\alpha + 2\beta - (\alpha + \beta ) = \beta \) گویاست که با فرض، تناقض دارد؛ پس \(\alpha + 2\beta \) گنگ است.
4 آیا اعدادی صحیح مانند x و y وجود دارند که:
\({x^2} + {y^2} = {\left( {x + y} \right)^2}\)
\(\begin{array}{l}{x^2} + {y^2} = {x^2} + {y^2} + 2xy \Rightarrow 2xy = 0\\\\ \Rightarrow x = 0\quad \vee \quad y = 0\end{array}\)
حداقل یکی از اعداد x و y باید صفر باشند؛ به طور مثال \(x = 0\) و \(y = 7\) جواب است.
5 آیا مقادیر حقیقی و ناصفر a و b چنان وجود دارند که:
\(\frac{1}{{a + b}} = \frac{1}{a} + \frac{1}{b}\;\;\;\;\;\left( {a + b \ne 0} \right)\)
خیر؛ اثبات :
برهان خلف : گیریم چنین اعدادی وجود داشته باشد، بنابراین :
\(\begin{array}{l}\frac{1}{{a + b}} = \frac{1}{a} + \frac{1}{b} \Rightarrow \frac{1}{{a + b}} = \frac{{a + b}}{{ab}}\\\\ \Rightarrow {(a + b)^2} = ab \Rightarrow {a^2} + {b^2} + 2ab = ab\\\\ \Rightarrow {a^2} + {b^2} + ab = 0\quad \mathop \Rightarrow \limits^{ \times 2} \quad 2{a^2} + 2{b^2} + 2ab = 0\\\\ \Rightarrow {(a + b)^2} + {a^2} + {b^2} = 0\\\\ \Rightarrow \quad a = 0\quad \wedge \quad b = 0\quad \wedge \quad a + b = 0\end{array}\)
که تناقض است.
6 گزاره های زیر را اثبات و یا با ارائه مثال نقض آنها را رد کنید.
الف مربع و مکعب هر عدد فرد عددی فرد است.
ب میانگین پنج عدد طبیعی متوالی همان عدد وسطی است.
الف
صحیح است؛ زیرا:
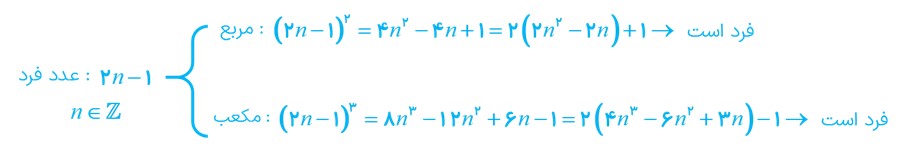
ب)
صحیح است؛ زیرا:
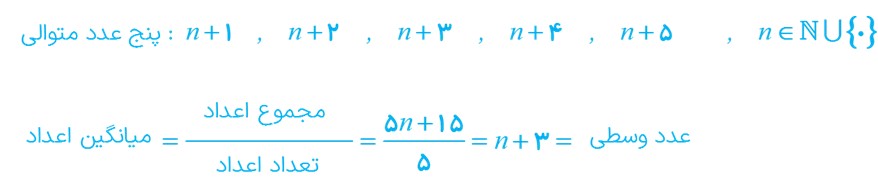
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















