جواب تمرین صفحه 76 درس 3 هندسه دوازدهم (بردارها)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 76 هندسه دوازدهم
-گام به گام تمرین صفحه 76 درس بردارها
-تمرین صفحه 76 درس 3
-شما در حال مشاهده جواب تمرین صفحه 76 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 چهار نقطه در دستگاه مختصات مقابل مشخص شدهاند.
الف معادلات مشخص کننده سطح محدود شده به چهارضلعی ABCD را بنویسید.
ب معادلات یکی از سطوحی که با سطح ABCD هممساحت و موازی هستند را بنویسید.
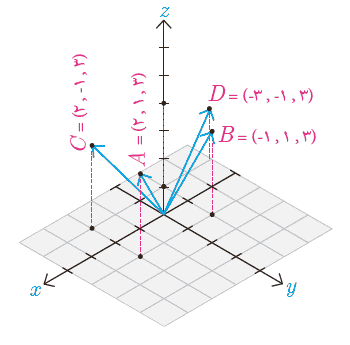
الف

\(\begin{array}{l}A(2\;,\;1\;,\;3)\;,\;B( - 1\;,\;1\;,\;3) \Rightarrow \\\\AB:\;(y = 1\;,\;z = 3\;;\; - 1 \le x \le 2)\\\\B( - 1\;,\;1\;,\;3)\;,\;D( - 3\;,\; - 1\;,\;3) \Rightarrow \\\\BD:\;(y = x + 2\;,\;z = 3\;;\; - 3 \le x \le - 1)\\\\D( - 3\;,\; - 1\;,\;3)\;,\;C(2\;,\; - 1\;,\;3) \Rightarrow \\\\DC:\;(y = - 1\;,\;z = 3\;;\; - 3 \le x \le 2)\\\\A(2\;,\;1\;,\;3)\;,\;C(2\;,\; - 1\;,\;3) \Rightarrow \\\\AC:\;(x = 2\;,\;z = 3\;;\; - 1 \le y \le 1)\end{array}\)
ب
\(\begin{array}{l}A'(2\;,\;1\;,\;0)\;,\;B'( - 1\;,\;1\;,\;0) \Rightarrow \\\\A'B':\;(y = 1\;,\;z = 0\;;\; - 1 \le x \le 2)\\\\B'( - 1\;,\;1\;,\;0)\;,\;D'( - 3\;,\; - 1\;,\;0) \Rightarrow \\\\B'D':\;(y = x + 2\;,\;z = 0\;;\; - 3 \le x \le - 1)\\\\D'( - 3\;,\; - 1\;,\;0)\;,\;C'(2\;,\; - 1\;,\;0) \Rightarrow \\\\D'C':\;(y = - 1\;,\;z = 0\;;\; - 3 \le x \le 2)\\\\A'(2\;,\;1\;,\;0)\;,\;C'(2\;,\; - 1\;,\;0) \Rightarrow \\\\A'C':\;(x = 2\;,\;z = 0\;;\; - 1 \le y \le 1)\end{array}\)
2 نقاط با مختصات P=(1, 0, 1) و Q=(0. -1. -2) و R=(3, 0, -1) و S=(-2, -2, -2) را در یک دستگاه مختصات نمایش دهید.

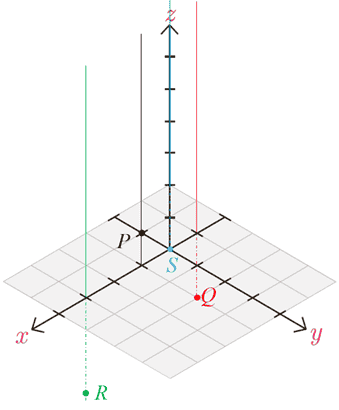
3 در سؤال قبل طول پاره خط های PQ و RQ و PS را بیابید.
\(\begin{array}{l}PQ = \sqrt {{{({x_Q} - {x_P})}^2} + {{({y_Q} - {y_P})}^2} + {{({z_Q} - {z_P})}^2}} \\\\ \Rightarrow PQ = \sqrt {{{(0 - 1)}^2} + {{( - 1 - 0)}^2} + {{( - 2 - 1)}^2}} \\\\ = \sqrt {1 + 1 + 9} = \sqrt {11} \\\\RQ = \sqrt {{{({x_Q} - {x_R})}^2} + {{({y_Q} - {y_R})}^2} + {{({z_Q} - {z_R})}^2}} \\\\ \Rightarrow RQ = \sqrt {{{(0 - 3)}^2} + {{( - 1 - 0)}^2} + {{( - 2 + 1)}^2}} \\\\ = \sqrt {9 + 1 + 1} = \sqrt {11} \\\\PS = \sqrt {{{({x_S} - {x_P})}^2} + {{({y_S} - {y_P})}^2} + {{({z_S} - {z_P})}^2}} \\\\ \Rightarrow SQ = \sqrt {{{( - 2 - 1)}^2} + {{( - 2 - 0)}^2} + {{( - 2 - 1)}^2}} \\\\ = \sqrt {9 + 4 + 9} = \sqrt {22} \end{array}\)
4 فرض کنید P=(x0, y0, z0) و Q=(x1, y1, z1) مختصات نقطه M وسط پاره خط PQ را بیابید.
\(\begin{array}{l}{x_M} = \frac{{{x_P} + {x_Q}}}{2}\\\\{y_M} = \frac{{{y_P} + {y_Q}}}{2}\\\\{z_M} = \frac{{{z_P} + {z_Q}}}{2}\\\\ \Rightarrow M(\frac{{{x_P} + {x_Q}}}{2}\;,\;\frac{{{y_P} + {y_Q}}}{2}\;,\;\frac{{{z_P} + {z_Q}}}{2})\end{array}\)
5 در هر کدام از حالات زیر بردار خواسته شده را بیابید.
الف
\(\begin{array}{l}r\overrightarrow a - \overrightarrow b = ?\;\;,\;\;r = 3\;\;,\;\;\overrightarrow b = \left( {\sqrt 2 ,\;1,\;1} \right)\;\;,\\\\\overrightarrow a = \left( { - \frac{1}{3},\;0,\;2} \right)\end{array}\)
ب
\(\begin{array}{l}r\overrightarrow a + \overrightarrow b = ?\;\;,\;\;r = - 1\;\;,\;\;\overrightarrow b = \left( {3,\;1,\; - 1} \right)\;\;,\\\\\overrightarrow a = 3\overrightarrow i + 2\overrightarrow j - \overrightarrow k \end{array}\)
ج
\(\overrightarrow a + \overrightarrow b = ?\;\;,\;\;\overrightarrow b = 3\overrightarrow j + \overrightarrow k \;\;,\;\;\overrightarrow a = \sqrt 2 \;\overrightarrow i - \overrightarrow k \)
د
\(\begin{array}{l}r\overrightarrow a + \overrightarrow b = ?\;\;,\;\;r = \frac{1}{5}\;\;,\;\;\overrightarrow b = - \overrightarrow k + \overrightarrow i \;\;,\\\\a = 5\overrightarrow k + \overrightarrow j \end{array}\)
الف
\(\begin{array}{l}r\overrightarrow a - \overrightarrow b = 3( - \frac{1}{3}\;,\;0\;,\;2) - (\sqrt 2 \;,\;1\;,\;1)\\\\ = ( - 1\;,\;0\;,\;6) - (\sqrt 2 \;,\;1\;,\;1)\\\\ = ( - \sqrt 2 - 1\;,\; - 1\;,\;5)\end{array}\)
ب
\(\begin{array}{l}r\overrightarrow a + \overrightarrow b = - 1(3\;,\;2\;,\; - 1) + (3\;,\;1\;,\; - 1)\\\\ = ( - 3\;,\; - 2\;,\;1) + (3\;,\;1\;,\; - 1)\\\\ = (0\;,\; - 1\;,\;0)\end{array}\)
ج
\(\begin{array}{l}\overrightarrow a + \overrightarrow b = (\sqrt 2 \;,\;0\;,\; - 1) + (0\;,\;3\;,\;1)\\\\ = (\sqrt 2 \;,\;3\;,\;0)\end{array}\)
د
\(\begin{array}{l}r\overrightarrow a + \overrightarrow b = \frac{1}{5}(0\;,\;1\;,\;5) + (1\;,\;0\;,\; - 1)\\\\ = (0\;,\;\frac{1}{5}\;,\;1) + (1\;,\;0\;,\; - 1) = (1\;,\;\frac{1}{5}\;,\;0)\end{array}\)
6 طول بردار a را در هر یک از حالات سؤال قبل بیابید.
الف
\(\begin{array}{l}\overrightarrow a = ( - \frac{1}{3}\;,\;0\;,\;2) \Rightarrow \\\\\left| {\overrightarrow a } \right| = \sqrt {{{( - \frac{1}{3})}^2} + {0^2} + {2^2}} \\\\ = \sqrt {\frac{{37}}{9}} = \frac{{\sqrt {37} }}{3}\end{array}\)
ب
\(\begin{array}{l}\overrightarrow a = (3\;,\;2\;,\; - 1) \Rightarrow \\\\\left| {\overrightarrow a } \right| = \sqrt {{3^2} + {2^2} + {{( - 1)}^2}} = \sqrt {14} \end{array}\)
ج
\(\begin{array}{l}\overrightarrow a = (\sqrt 2 \;,\;0\;,\; - 1) \Rightarrow \\\\\left| {\overrightarrow a } \right| = \sqrt {{{(\sqrt 2 )}^2} + {0^2} + {{( - 1)}^2}} = \sqrt 3 \end{array}\)
د
\(\begin{array}{l}\overrightarrow a = (0\;,\;1\;,\;5) \Rightarrow \\\\\left| {\overrightarrow a } \right| = \sqrt {{0^2} + {1^2} + {5^2}} = \sqrt {26} \end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















