شاه کلید نکات
شاه کلید سوال
1 تصویر بردار I = (1, 0, 0) بر امتداد بردار j = (0, 1, 0) را بیابید.
\(\begin{array}{l}\left. \begin{array}{l}\overrightarrow i = (1\;,\;0\;,\;0)\;,\;\overrightarrow j = (0\;,\;1\;,\;0)\\\\\overrightarrow i \cdot \overrightarrow j = 1 \times 0 + 0 \times 1 + 0 \times 0 = 0\;\\\\{\left| {\overrightarrow j } \right|^2} = {0^2} + {1^2} + {0^2} = 1\end{array} \right\}\\\\ \Rightarrow \overrightarrow {i'} = \frac{{\overrightarrow i \cdot \overrightarrow j }}{{{{\left| {\overrightarrow j } \right|}^2}}}\overrightarrow j = \frac{0}{1}(0\;,\;1\;,\;0) = (0\;,\;0\;,\;0) = \overrightarrow O \end{array}\)
2 نشان دهید که اگر دو بردار a و b بر هم عمود باشند، آنگاه تصویر یکی بر امتداد دیگری بردار صفر می شود.
فرض کنیم
\(\overrightarrow b = ({b_1}\;,\;{b_2}\;,\;{b_3}) \ne \overrightarrow O \;,\;\overrightarrow a = ({a_1}\;,\;{a_2}\;,\;{a_3}) \ne \overrightarrow O \) و \(\overrightarrow a \bot \overrightarrow b \)
در این صورت \(\overrightarrow a \cdot \overrightarrow b = \;\;0\) و تصویر \(\overrightarrow a \) بر \(\overrightarrow b \) برابر است با :
\(\begin{array}{l}\left. \begin{array}{l}\overrightarrow i = (1\;,\;0\;,\;0)\;,\;\overrightarrow j = (0\;,\;1\;,\;0)\\\\\overrightarrow i \cdot \overrightarrow j = 1 \times 0 + 0 \times 1 + 0 \times 0 = 0\;\\\\{\left| {\overrightarrow j } \right|^2} = {0^2} + {1^2} + {0^2} = 1\end{array} \right\}\\\\ \Rightarrow \overrightarrow {a'} = \frac{{\overrightarrow a \cdot \overrightarrow b }}{{{b^2}}}\overrightarrow b = \frac{0}{{{b^2}}}({b_1}\;,\;{b_2}\;,\;{b_3})\\\\ = (0\;,\;0\;,\;0) = \overrightarrow O \end{array}\)
3 نشان دهید اگر بردار a و b در یک راستا باشند آنگاه تصویر a بر b برابر خود a می شود.
فرض کنیم
\(\overrightarrow b = ({b_1}\;,\;{b_2}\;,\;{b_3}) \ne \overrightarrow O \;,\;\overrightarrow a = ({a_1}\;,\;{a_2}\;,\;{a_3}) \ne \overrightarrow O \) و \(\overrightarrow a = k\overrightarrow b \)
در این صورت :
\(\overrightarrow a \cdot \overrightarrow b = k\overrightarrow b \cdot \overrightarrow b = k{b^2}\)
تصویر \(\overrightarrow a \) بر \(\overrightarrow b \) برابر است با :
\(\overrightarrow {a'} = \frac{{\overrightarrow a \cdot \overrightarrow b }}{{{b^2}}}\overrightarrow b = \frac{{k\overrightarrow b \cdot \overrightarrow b }}{{{b^2}}}\overrightarrow b = \frac{{k{b^2}}}{{{b^2}}}\overrightarrow b = k\overrightarrow b = \overrightarrow a \)
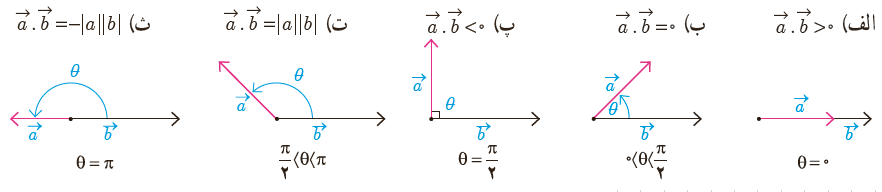
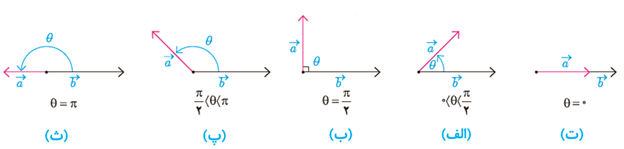
4 هر یک از حالات زیر را با شکل های داده شده نظیر کنید.
1736019749.png)
