جواب تمرین صفحه 57 درس 2 هندسه دوازدهم (آشنایی با مقاطع مخروطی)
تعداد بازدید : 86.34Mپاسخ تمرین صفحه 57 هندسه دوازدهم
-گام به گام تمرین صفحه 57 درس آشنایی با مقاطع مخروطی
-تمرین صفحه 57 درس 2
-شما در حال مشاهده جواب تمرین صفحه 57 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
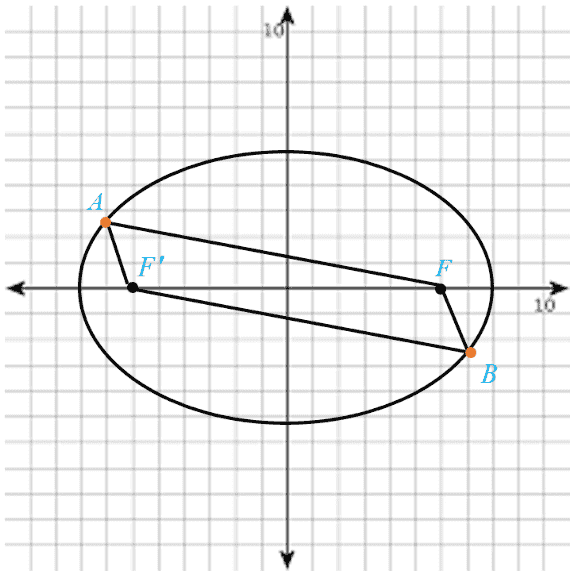
1 دو نقطه \(A\) و \(B\) روی یک بیضی و \(F\) و \(F’\) کانون های بیضی اند. \(A\) به کانون \(F’\) نزدیک تر و \(B\) به کانون \(F\) نزدیکتر است. اگر \(AF’=BF\) باشد، نشان دهید:
الف در حالتی که دو پاره خط \(AF\) و \(BF’\) یکدیگر را درون بیضی قطع نکنند، با هم موازی اند.
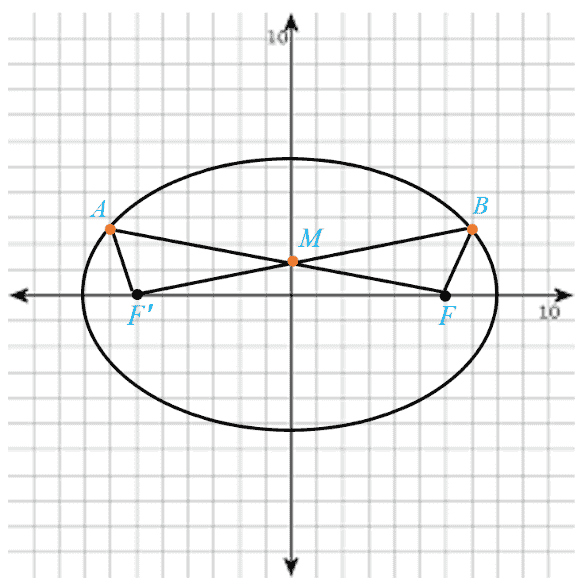
ب در حالتی که \(AF\) و \(BF’\) یکدیگر را درون بیضی و در نقطه ای مانند \(M\) قطع کنند، مثلث \(FMF’\) متساوی الساقین است و \(M\) روی قطر کوچک بیضی است.
الف اگر \(BF'\) و \(AF\) یکدیگر را درون دایره قطع نکنند، چهارضلعی \(AFBF'\) را در نظر می گیریم. نقاط \(B\) و \(A\) روی بیضی قرار دارند، پس :
\(\begin{array}{l}AF + AF' = BF + BF' = 2a\\\\\mathop \Rightarrow \limits^{AF' = BF} \;\;AF + BF = BF + BF'\\\\ \Rightarrow AF = BF'\end{array}\)
به عبارت ئیگر در چهارضلعی \(AFBF'\) اضلاع مقابل دو به دو مساویند، لذا چهارضلعی \(AFBF'\) متوازی الاضلاع است. پس : \(AF\parallel BF'\)
ب اگر \(BF'\) و \(AF\) روی بیضی قرار دارند، پس :
\(\begin{array}{*{20}{l}}{AF + AF' = BF + BF' = 2a}\\{}\\{\mathop \Rightarrow \limits^{BF = AF'} \:\:AF + BF = BF + BF'}\\{}\\{ \Rightarrow AF = BF'}\\{}\\{\left\{ {\begin{array}{*{20}{l}}{AF' = BF}\\{}\\{AF = BF'}\\{}\\{FF' = FF'}\end{array}} \right.}\\{}\\{ \Rightarrow A\mathop F\limits^\Delta F' \cong B\mathop F\limits^\Delta F'}\\{}\\{ \Rightarrow \mathop A\limits^ \wedge = \mathop B\limits^ \wedge }\\{}\\{\left\{ {\begin{array}{*{20}{l}}{\mathop A\limits^ \wedge = \mathop B\limits^ \wedge }\\{}\\{\mathop {\;{M_1}}\limits^ \wedge = \mathop {\;{M_2}}\limits^ \wedge }\\{}\\{AF' = BF}\end{array}} \right.}\\{}\\{ \Rightarrow A\mathop M\limits^\Delta F' \cong B\mathop M\limits^\Delta F}\\{}\\{ \Rightarrow MF' = MF}\end{array}\)
از طرف دیگر قطر کوچک بیضی عمود منصف پاره خط \(FF'\) می باشد. لذا از رأس \(M\) در مثلث متساوی الساقین \(FMF'\) می گذرد.
2 قطر دایره \(C\) مانند شکل، قطر بزرگ بیضی \(e\) است و از کانون \(F\) عمودی بر \(AA’\) رسم کرده ایم تا دایره را در نقطه ای مانند \(M\) قطع کند. ثابت کنید \(MF\) با نصف قطر کوچک بیضی برابر است.
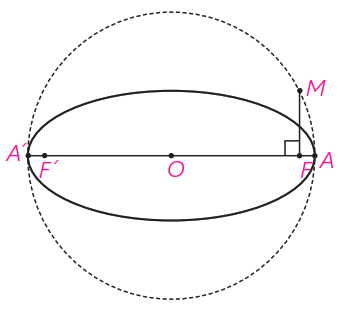
در مثلث قائم الزاویه \(\triangle OFM\) داریم:
\(\begin{array}{l}O\mathop F\limits^\Delta M:\quad \mathop F\limits^ \wedge = {90^ \circ }\\\\ \Rightarrow F{M^2} = O{M^2} - O{F^2}\\\\\mathop \Rightarrow \limits_{OF = c}^{OM = a} \;F{M^2} = {a^2} - {c^2}\\\\\mathop \Rightarrow \limits^{{a^2} - {c^2} = {b^2}} F{M^2} = {b^2}\\\\ \Rightarrow FM = b\end{array}\)
بنابراین \(FM\) برابر با نصف قطر کوچک (b) است.
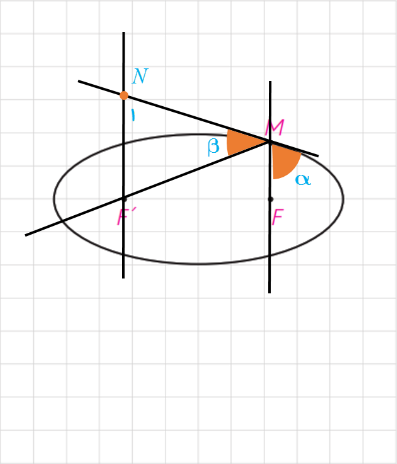
3 در شکل مقابل نقطه \(M\) روی بیضی و کانون های \(F\) و \(F’\) مشخص شده اند. خط \(d\) را به گونه ای رسم کنید که در نقطه \(M\) بر بیضی مماس باشد و سپس از نقطه \(F’\) خطی موازی با \(MF\) رسم کنید تا خط \(d\) را در نقطه ای مانند \(N\) قطع کند. ثابت کنید \(NF’ = MF’\)
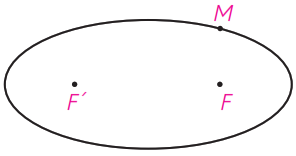
بنابر خاصیت بازتابندگی بیضی، خط مماس \(d\) در نقطه \(M\) ، نیمساز زاویه خارجی \(\angle FMF'\) است. به عبارت دیگر، زاویه بین \(MF\) و خط مماس برابر با زاویه بین \(MF'\) و خط مماس است. این زاویه را \(\beta\) می نامیم (یعنی زاویه تابش برابر زاویه بازتابش است).
فرض کنیم زاویه بین \(MF\) و خط مماس \(d\) برابر \(\alpha\) باشد. پس بنابر خاصیت بازتابندگی، زاویه بین \(MF'\) و خط مماس \(d\) نیز \(\alpha\) است. (\(\beta = \alpha\) در شکل متن اصلی)
خط \(F'N\) موازی با \(MF\) رسم شده است (\(FM \parallel F'N\) ) و خط \(d\) (یا همان \(MN\) ) مورب است. بنابراین زاویه \(\angle MNF'\) (که \(\angle N_1\) نامیده شده) با زاویه بین \(MF\) و خط مماس \(d\) برابر است (زوایای متبادل داخلی). پس \(\angle N_1 = \alpha\) .
در مثلث \(\triangle F'MN\) ، زاویه \(\angle F'MN\) (زاویه بین \(MF'\) و خط مماس) برابر \(\alpha\) است و زاویه \(\angle MNF'\) (\(\angle N_1\) ) نیز برابر \(\alpha\) شد.
چون در مثلث \(\triangle F'MN\) دو زاویه \(\angle F'MN\) و \(\angle MNF'\) برابر هستند، این مثلث متساوی الساقین است و اضلاع مقابل به این زوایا برابرند. یعنی \(NF' = MF’\) .
4 نقطه \(M\) روی بیضی به اقطار 6 و 10 واحد به گونه ای قرار دارد که فاصله آن تا مرکز بیضی برابر 4 واحد است.
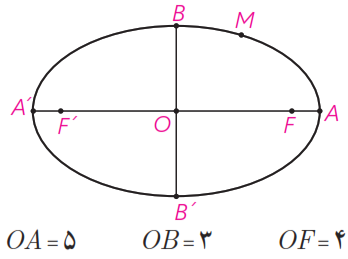
الف نشان دهید \(OM = OF = OF’\)
ب نشان دهید مثلث \(MFF’\) قائم الزاویه است.
ج طول های \(MF\) و \(MF’\) را به دست آورید.
الف
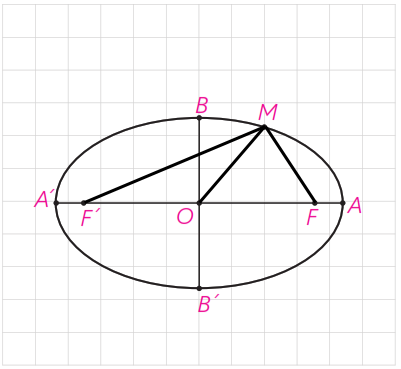
\(\begin{array}{l}\left\{ \begin{array}{l}AA' = 10 \Rightarrow 2a = 10 \Rightarrow a = 5\\\\BB' = 6 \Rightarrow 2b = 6 \Rightarrow b = 3\end{array} \right.\\\\ \Rightarrow {c^2} = {a^2} - {b^2} = {5^2} - {3^2} = \\\\25 - 9 = 16\\\\ \Rightarrow c = 4\\\\OF = OF' = OM = 4\end{array}\)
ب در مثلث MFF' میانه OM نصف ضلع FF' است؛ پس مثلث در رأس M قائمه است:
\(\begin{array}{l}M\mathop F\limits^\Delta F':\\\\OM = OF = OF' = \frac{1}{2}FF'\\\\ \Rightarrow \mathop M\limits^ \wedge = {90^ \circ }\end{array}\)
ج طبق تعریف بیضی، برای نقطه روی بیضی داریم: .
از بخش (ب) می دانیم مثلث قائم الزاویه است، پس طبق قضیه فیثاغورس:
\(\begin{array}{l}MF + MF' = 2a = 10\\\\ \Rightarrow MF' = 10 - MF\\\\M\mathop F\limits^\Delta F':\quad \mathop M\limits^ \wedge = {90^ \circ }\\\\ \Rightarrow M{F^2} + M{{F'}^2} = F{{F'}^2}\\\\ \Rightarrow M{F^2} + {(10 - MF)^2} = {8^2}\\\\\mathop \Rightarrow \limits^{MF = x} \;\;{x^2} + {(10 - x)^2} = 64\\\\ \Rightarrow {x^2} + 100 - 20x + {x^2} - 64 = 0\\\\ \Rightarrow 2{x^2} - 20x + 36 = 0\\\\ \Rightarrow {x^2} - 10x + 18 = 0\\\\ \Rightarrow x = 5 \pm \sqrt 7 \Rightarrow MF = x\\\\\mathop \Rightarrow \limits^{if} MF = 5 + \sqrt 7 \\\\ \Rightarrow MF' = 5 - \sqrt 7 \\\\\mathop \Rightarrow \limits^{else} MF = 5 - \sqrt 7 \\\\ \Rightarrow MF' = 5 + \sqrt 7 \end{array}\)
5 در بیضی مقابل طول قطر بزرگ دو برابر طول قطر کوچک است. اندازه زاویه چند درجه است؟
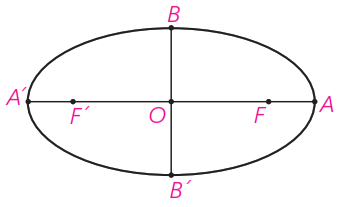
طول قطر بزرگ و طول قطر کوچک است.
طبق فرض مسئله: .
\(\begin{array}{l}AA' = 2BB' \Rightarrow a = 2b\\\\{c^2} = {a^2} - {b^2}\\\\ \Rightarrow {c^2} = {(2b)^2} - {b^2} = 3{b^2}\\\\ \Rightarrow c = \sqrt 3 b\\\\ \Rightarrow \frac{c}{b} = \sqrt 3 \\\\B\mathop O\limits^\Delta F:\\\\\tan (\hat B) = \frac{{OF}}{{BF}} = \frac{c}{b} = \sqrt 3 \\\\ \Rightarrow O\mathop B\limits^ \wedge F = O\mathop B\limits^ \wedge F' = {60^ \circ }\\\\ \Rightarrow F'\mathop B\limits^ \wedge F = {120^ \circ }\end{array}\)
بنابراین اندازه زاویه برابر 120 درجه است.
6 در بیضی مقابل و دو قطراند. خط در نقطه بر بیضی مماس است. پاره خط را رسم می کنیم و در نقطه عمودی بر رسم می کنیم تا خط را در نقطه قطع کند و از عمودی بر امتداد قطر بزرگ بیضی رسم می کنیم تا آن را در نقطه ای مانند قطع کند. اگر زاویه ، مقدار را به دست آورید.
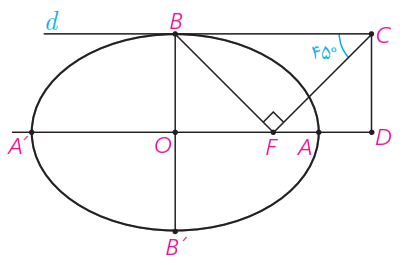
\(\begin{array}{l}\left. \begin{array}{l}BB' \bot d\\\\BB' \bot AA'\end{array} \right\} \Rightarrow d \bot AA'\\\\B\mathop C\limits^\Delta F:\quad \mathop F\limits^ \wedge = {90^ \circ }\;,\;\mathop C\limits^ \wedge = {45^ \circ }\\\\ \Rightarrow \mathop {{B_1}}\limits^ \wedge = {45^ \circ }\\\\ \Rightarrow \mathop {{B_2}}\limits^ \wedge = \mathop {{F_1}}\limits^ \wedge = {45^ \circ }\\\\ \Rightarrow OB = OF \Rightarrow b = c\\\\\mathop \Rightarrow \limits^{{a^2} = {b^2} + {c^2}} \;\;\;{a^2} = {c^2} + {c^2} = 2{c^2}\\\\ \Rightarrow a = \sqrt 2 c\\\\\frac{{OF}}{{OA}} = \frac{c}{a}\\\\ \Rightarrow \frac{{OF}}{{OA - OF}} = \frac{c}{{a - c}}\\\\ \Rightarrow \frac{{OF}}{{OA}} = \frac{c}{{\sqrt 2 c - c}} = \\\\\frac{1}{{\sqrt 2 - 1}} = \sqrt 2 + 1\\\\ \Rightarrow \frac{{OF}}{{OA}} = \sqrt 2 + 1\\\\O\mathop B\limits^\Delta F \cong F\mathop C\limits^\Delta D\\\\ \Rightarrow OF = DF\\\\ \Rightarrow \frac{{DF}}{{AF}} = \sqrt 2 + 1\\\\ \Rightarrow \frac{{DF - AF}}{{AF}} = \frac{{\sqrt 2 + 1 - 1}}{1}\\\\ \Rightarrow \frac{{AD}}{{AF}} = \sqrt 2 \end{array}\)
7 سهمی مفروض است. مختصات رأس و کانون سهمی را یافته و آن را رسم کنید. همچنین مختصات نقاط برخورد سهمی و محورهای مختصات را بیابید.
معادله را به صورت استاندارد در می آوریم:
\(\begin{array}{*{20}{l}}{y = a{x^2} + bx + c}\\{}\\{ \Rightarrow y - c = a\;({x^2} + \frac{b}{a}x)}\\{}\\{ \Rightarrow y - c = a\;({x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}})}\\{}\\{ \Rightarrow y - c = a\;{{(x + \frac{b}{{2a}})}^2} - \frac{{{b^2}}}{{4a}}}\\{}\\{ \Rightarrow y - c + \frac{{{b^2}}}{{4a}} = a\;{{(x + \frac{b}{{2a}})}^2}}\\{}\\{ \Rightarrow y - \frac{{4ac - {b^2}}}{{4a}} = a\;{{(x - \frac{{ - b}}{{2a}})}^2}}\\{}\\{ \Rightarrow 4p = a\;\; \Rightarrow p = \frac{a}{4}}\\{}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{S\left| {\begin{array}{*{20}{l}}{\alpha = \frac{{ - b}}{{2a}}}\\{}\\{\beta = \frac{{4ac - {b^2}}}{{4a}}}\end{array}} \right.}\\{}\\{F\left| {\begin{array}{*{20}{l}}{\alpha = \frac{{ - b}}{{2a}}}\\{}\\{\beta + p = \frac{{4ac - {b^2}}}{{4a}} + \frac{a}{4}}\end{array}} \right.}\end{array}} \right.}\\{}\\{ \Rightarrow F(\frac{{ - b}}{{2a}}\;,\;\frac{{{a^2} + 4ac - {b^2}}}{{4a}})}\\{}\\{y = \beta - p = }\\{}\\{\frac{{4ac - {b^2}}}{{4a}} - \frac{a}{4} = \frac{{4ac - {b^2} - {a^2}}}{{4a}}}\end{array}\)
8 مختصات رأس و کانون سهمی به معادله را به دست آورید.
\(\begin{array}{*{20}{l}}{y = a{x^2} + bx + c}\\{}\\{ \Rightarrow y - c = a\;({x^2} + \frac{b}{a}x)}\\{}\\{ \Rightarrow y - c = a\;({x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}})}\\{}\\{ \Rightarrow y - c = a\;{{(x + \frac{b}{{2a}})}^2} - \frac{{{b^2}}}{{4a}}}\\{}\\{ \Rightarrow y - c + \frac{{{b^2}}}{{4a}} = a\;{{(x + \frac{b}{{2a}})}^2}}\\{}\\{ \Rightarrow y - \frac{{4ac - {b^2}}}{{4a}} = a\;{{(x - \frac{{ - b}}{{2a}})}^2}}\\{}\\{ \Rightarrow 4p = a\;\; \Rightarrow p = \frac{a}{4}}\\{}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{S\left| {\begin{array}{*{20}{l}}{\alpha = \frac{{ - b}}{{2a}}}\\{}\\{\beta = \frac{{4ac - {b^2}}}{{4a}}}\end{array}} \right.}\\{}\\{F\left| {\begin{array}{*{20}{l}}{\alpha = \frac{{ - b}}{{2a}}}\\{}\\{\beta + p = \frac{{4ac - {b^2}}}{{4a}} + \frac{a}{4}}\end{array}} \right.}\end{array}} \right.}\\{}\\{ \Rightarrow F(\frac{{ - b}}{{2a}}\;,\;\frac{{{a^2} + 4ac - {b^2}}}{{4a}})}\\{}\\{y = \beta - p = }\\{}\\{\frac{{4ac - {b^2}}}{{4a}} - \frac{a}{4} = \frac{{4ac - {b^2} - {a^2}}}{{4a}}}\end{array}\)
9 معادله سهمی را بنویسید که رأس و کانون آن باشد.
پاسخ کوتاه:
\(S(1\;,\;2) \Rightarrow \alpha = 1\;,\;\beta = 2\)
چون S و F ، طول های برابر دارند و نقطه S در صفحه مختصات بالاتر از F قرار دارد، سهمی قائم می باشد و تقعر آن رو به پایین است؛ لذا :
\(\begin{array}{l}F(1\;,\; - 2) \Rightarrow \left\{ \begin{array}{l}\alpha = 1\\\\\beta - \alpha = - 2\end{array} \right.\\\\ \Rightarrow 2 - \alpha = - 2 \Rightarrow \underline {\alpha = 4 > 0} \\\\{(x - \alpha )^2} = - 4\alpha (y - \beta )\\\\ \Rightarrow {(x - 1)^2} = - 16(y - 2)\end{array}\)
پاسخ کاملتر:
رأس \(S(1,2)\) پس \(\alpha=1, \beta=2\)
کانون \(F(1,-2)\) .
چون طول رأس و کانون یکسان است (x=1)، سهمی قائم است. محور تقارن آن خط x=1 است.
چون عرض کانون (2-) از عرض رأس (2) کمتر است، دهانه سهمی رو به پایین باز می شود.
فاصله رأس تا کانون برابر |P| است: \(|p| = |y_F - y_S| = |-2 - 2| = |-4| = 4\)
چون دهانه رو به پایین است، p منفی است، پس p=-4 .
معادله سهمی قائم: \({(x-\alpha)^2} = 4p(y-\beta)\)
\({(x-1)^2} = 4(-4)(y-2)\)
\({(x-1)^2} = -16(y-2)\)
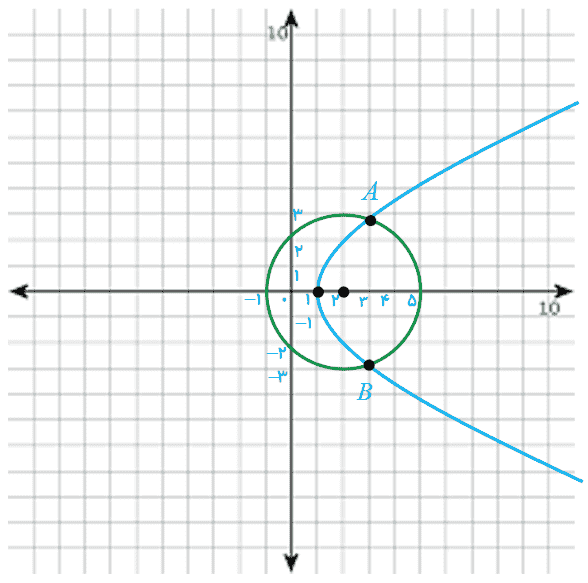
10 سهمی مفروض است. به مرکز کانون سهمی و به شعاع 3 واحد دایره ای رسم می کنیم، مختصات نقاط برخورد دایره و سهمی را بیابید.
\(\begin{array}{l}{y^2} = 4x - 4 \Rightarrow {(y - 0)^2} = 4(x - 1)\\\\ \Rightarrow \left\{ \begin{array}{l}\alpha = 1\\\\\beta = 0\\\\4a = 4 \Rightarrow a = 1\end{array} \right.\\\\ \Rightarrow F(\alpha + a\;,\;\beta ) \Rightarrow F(2\;,\;0)\\\\{(x - 2)^2} + {(y - 0)^2} = {3^2}\\\\ \Rightarrow {(x - 2)^2} + {y^2} = 9\\\\\mathop \Rightarrow \limits^{{y^2} = 4x - 4} \;\;{(x - 2)^2} + 4x - 4 = 9\\\\ \Rightarrow {x^2} - 4x + 4 + 4x - 4 = 9\\\\ \Rightarrow {x^2} = 9\\\\ \Rightarrow x = \pm 3\\\\if\,\,\,x = 3:\\\\ \Rightarrow {y^2} = 4(3) - 4 = 8\\\\ \Rightarrow y = \pm \sqrt 8 \\\\ \Rightarrow A(3\;,\;\sqrt 8 )\;,\;B(3\;,\; - \sqrt 8 )\\\\else\,\,\,x = - 3:\\\\ \Rightarrow {y^2} = 4( - 3) - 4 = - 16\end{array}\)
11 سهمی با کانون و خط هادی مفروض است. ثابت کنید مرکز هر دایره که از بگذرد و بر خط مماس باشد روی سهمی است و برعکس هر نقطه روی سهمی، مرکز یک دایره است که از گذشته و بر مماس است. با توجه به این موضوع تعریف دیگری از سهمی ارائه دهید.
فرض کنیم نقطه A نقطه دلخواهی روی سهمی باشد. به مرکز A و شعاع AF دایره ای رسم می کنیم. بنا به تعریف سهمی، هر نقطه روی سهمی از کانون و خط هادی آن به یک فاصله است؛ پس دایره رسم شده باید بر خط d مماس باشد.
بالعکس فرض می کنیم دایره C(A,r) از F می گذرد و بر خط در نقطه H مماس است. بدیهی است که AF=AH=r ؛ پس نقطه A از کانون و خط هادی سهمی به یک فاصله است؛ لذا A روی سهمی قرار دارد.
نتیجه:
هر سهمی، مکان هندسی مرکز دایره ای از صفحه است که از یک نقطه ثابت آن صفحه می گذرد و بر یک خط ثابت از آن صفحه مماس است.
12 در شکل سهمی با رأس و کانون و خط هادی رسم شده است. از به نقطه دلخواه روی سهمی وصل کرده و امتداد داده ایم تا را در قطع کند و از نقطه ، را بر عمود کرده ایم. ثابت کنید:
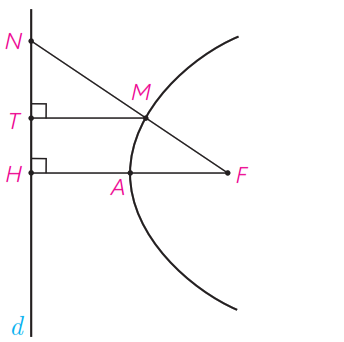
A و M دو نقطه روی سهمی اند، پس فاصله آن ها از کانون و خط هادی سهمی برابر است؛ یعنی :
\(\begin{array}{l}\left\{ \begin{array}{l}MT = MF\\\\AH = AF\end{array} \right. \Rightarrow FH = 2AH\\\\F\mathop N\limits^\Delta H:\\\\TM\parallel FH\;\; \Rightarrow \;\;\frac{{TM}}{{FH}} = \frac{{NM}}{{NF}}\\\\\mathop \Rightarrow \limits_{FH = 2FA}^{TM = MF} \;\;\;\frac{{MF}}{{2FA}} = \frac{{NM}}{{NF}}\\\\ \Rightarrow \frac{{NF}}{{2FA}} = \frac{{NM}}{{MF}}\quad (1)\\\\F\mathop N\limits^\Delta H:\\\\TM\parallel FH \Rightarrow \frac{{TN}}{{TH}} = \frac{{NM}}{{MF}}\quad (2)\\\\(1)\;,\;(2) \Rightarrow \frac{{NF}}{{2FA}} = \frac{{TN}}{{TH}}\\\\\mathop \Rightarrow \limits^{ \times \,2} \frac{{FN}}{{FA}} = \frac{{2NT}}{{TH}}\end{array}\)
13 یک دانش آموز با دیدن دو دیش مخابراتی با ابعاد متفاوت و مشاهده فاصله کانونی متفاوت آنها به این فکر افتاد که چگونه می توان با داشتن یک دیش فاصله کانونی آن را به دست آورد. او از معلمش خواست که فرمولی برای محاسبه فاصله کانونی یک دیش به او بگوید. معلم به او گفت: باید قطر دهانه دیش را در خودش ضرب کرد و حاصل ضرب را بر اندازه گودی (عمق) دیش تقسیم کرد و عدد حاصل را بر 16 تقسیم کرد. حاصل فاصله کانونی دیش است. دلیل درستی این دستور را با توجه به سهمی رسم شده در شکل مقابل و فرمول سهمی توضیح دهید.
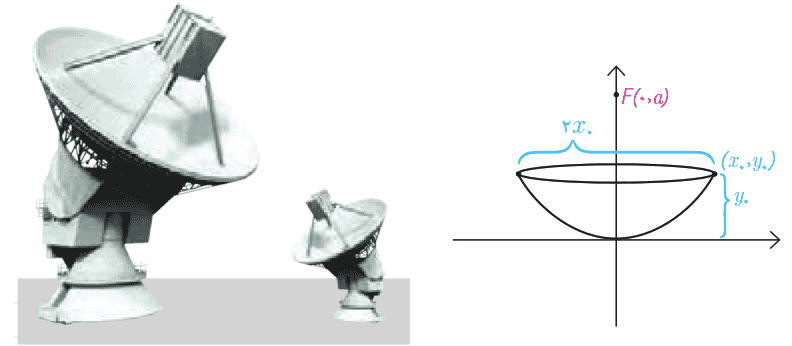
با توجه به شکل، سهمی داده شده، قائم است و رأس آن مبدأ مختصات می باشد؛ پس معادله آن به صورت مقابل است: \({x^2} = 4a\;y\)
اگر \(({x_ \circ }\;,\;{y_ \circ })\) نقطه ای روی سهمی باشد، به راحتی می توان فاصله کانونی را به شکل مقابل حساب نمود:
\({x_ \circ }^2 = 4a\;{y_ \circ } \Rightarrow a = \frac{{4{y_ \circ }}}{{{x_ \circ }^2}}\)
حال به روش ارائه شده بپردازیم:
قطر دهانه دیش \(2{x_ \circ }\) و عمق دیش \({y_ \circ }\) است؛ پس بنا به روش مسأله داریم:
\(\frac{{\frac{{2{x_ \circ } \times 2{x_ \circ }}}{{{y_ \circ }}}}}{{16}} = \frac{{4{x_ \circ }^2}}{{16{y_ \circ }}} = \frac{{{x_ \circ }^2}}{{4{y_ \circ }}} = a\)
14 فرض کنید از مثلث اندازه ضلع و ارتفاع و محیط مثلث، داده شده باشد، با استفاده از خواص بیضی شیوه رسم این مثلث را توضیح دهید.
پاسخ کوتاه:
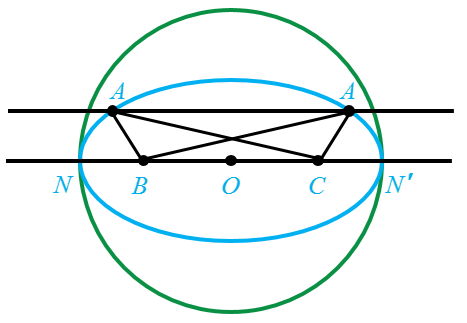
فرض کنیم BC=a و AH=ho و محیط مثلث ABC برابر 2p باشد. پاره خط BC=a را رسم نموده و وسط آن را O می نامیم. دایره ای به مرکز O و قطر 2p=a رسم می کنیم و BC را امتداد می دهیم تا دایره را در نقاط N و N' قطع کند. سپس یک بیضی به کانون های B و C که از N یا N' بگذرد. بدیهی است که NN' قطر بزرگ بیضی است و NN'=2p-a.
اگر A نقطه ی دلخواهی از بیضی باشد:
\(\begin{array}{l}AB + AC = NN'\\\\ \Rightarrow AB + AC = 2p - a\\\\ \Rightarrow AB + AC + BC = \\\\2p - a + a = 2p\end{array}\)
از نقطه N عمود MN=ho را از NN' خارج نموده و از M خط موازی NN' را رسم می کنیم. محل تقاطع خط و بیضی را A می نامیم و مثلث ABC را رسم می کنیم. مثلث ABC پاسخ مسأله است.
15 سهمی و دو خط موازی و را که با سهمی متقاطع اند، درنظر بگیرید.
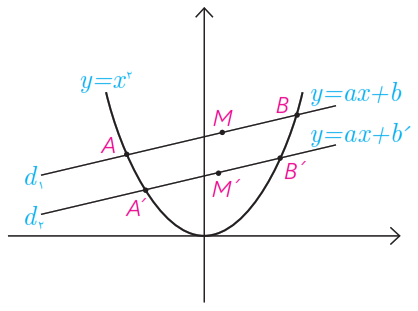
الف معادله درجه دومی تشکیل دهید که ریشه های آن طول نقاط برخورد خط و سهمی باشد.
ب فرض کنید و نقاط برخورد خط و سهمی باشند و نقطه وسط پاره خط باشد، مختصات نقطه را به دست آورید.
پ مراحل (الف) و (ب) را با جایگذاری خط به جای انجام دهید و مختصات نقطه (نقطه وسط پاره خط حاصل از نقاط تقاطع خط و سهمی) را به دست آورید.
ت خط نسبت به محور ها چه وضعی دارد؟
ث با استفاده از نتایج قسمتهای قبل روشی برای رسم محور تقارن یک سهمی با داشتن نمودار آن ارائه دهید و با این روش محور تقارن سهمی مقابل را رسم کنید.
الف برای یافتن نقاط برخورد \(y=x^2\) و \(y=ax+b\) ، آنها را مساوی قرار می دهیم:
\(x^2 = ax + b\)
\(x^2 - ax - b = 0\)
این معادله درجه دومی است که ریشه های آن (\(x_A\) و \(x_B\) ) طول نقاط برخورد هستند.
ب مختصات نقاط برخورد \(A(x_A, y_A)\) و \(B(x_B, y_B)\) هستند. نقطه M وسط AB است.
طول نقطه M :
\(x_M = \frac{x_A + x_B}{2}\)
از معادله \(x^2 - ax - b = 0\) ، مجموع ریشه ها برابر \(x_A + x_B = -(\frac{-a}{1}) = a\) است.
\(x_M = \frac{a}{2}\)
عرض نقطه M :
\(y_M = \frac{y_A + y_B}{2}\)
چون نقاط A و B روی خط y = ax + b هستند، \(y_A = ax_A + b\) و \(y_B = ax_B + b\) .
\(\begin{array}{l}{y_M} = \frac{{(a{x_A} + b) + (a{x_B} + b)}}{2} = \frac{{a({x_A} + {x_B}) + 2b}}{2}\\\\ = \frac{{a(a) + 2b}}{2} = \frac{{{a^2} + 2b}}{2}\end{array}\)
(روش دیگر: \(y_A = x_A^2\) و \(y_B = x_B^2\) . \(y_M = \frac{x_A^2 + x_B^2}{2} = \frac{(x_A+x_B)^2 - 2x_A x_B}{2}\) . حاصلضرب ریشه ها \(x_A x_B = \frac{-b}{1} = -b\) . \(y_M = \frac{a^2 - 2(-b)}{2} = \frac{a^2+2b}{2}\) )
پس مختصات \(M(\frac{a}{2}, \frac{a^2 + 2b}{2})\) است.
پ برای خط \(d_2: y = ax + b'\) ، معادله برخورد \(x^2 - ax - b' = 0\) است.
نقاط برخورد \(A'(x_{A'}, y_{A'})\) و \(B'(x_{B'}, y_{B'})\) .
نقطه وسط 'M .
مجموع ریشه های معادله \(x^2 - ax - b' = 0\) برابر \(x_{A'} + x_{B'} = a\) است.
\(x_{M'} = \frac{x_{A'} + x_{B'}}{2} = \frac{a}{2}\)
عرض 'M :
\(\begin{array}{l}{y_{M'}} = \frac{{{y_{A'}} + {y_{B'}}}}{2} = \frac{{(a{x_{A'}} + b') + (a{x_{B'}} + b')}}{2}\\\\ = \frac{{a({x_{A'}} + {x_{B'}}) + 2b'}}{2} = \frac{{a(a) + 2b'}}{2} = \frac{{{a^2} + 2b'}}{2}\end{array}\)
پس مختصات \(M'(\frac{a}{2}, \frac{a^2 + 2b'}{2})\) است.
ت طول نقاط و هر دو برابر \(\frac{a}{2}\) است (\(x_M = x_{M'} = \frac{a}{2}\)).
بنابراین خط یک خط قائم (عمودی) به معادله \(x = \frac{a}{2}\) است. این خط موازی محور ها است.
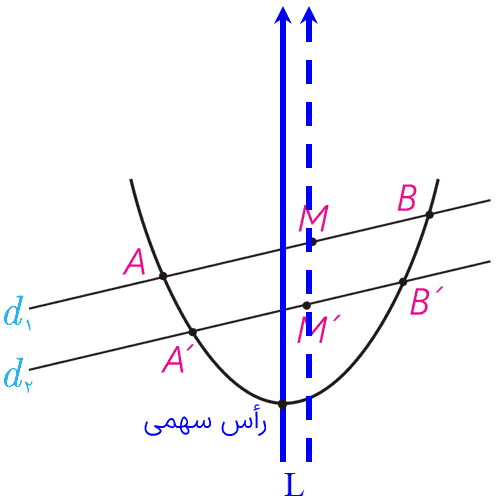
ث ابتدا دو خط موازی d و d' را چنان رسم می کنیم که سهمی را در نقاط A و B و A' و B' قطع کند. سپس وسط پاره خط های AB و A'B' را به ترتیب M و M' می نامیم.
از رأس سهمی خط L را موازی MM' رسم می کنیم. خط L پاسخ مسأله است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















