شاه کلید نکات
شاه کلید سوال
بیضی مقابل را درنظر بگیرید. ′AA قطر بزرگ (قطر کانونی) و ′BB قطر کوچک بیضی نامیده می شود. F و ′F کانون های بیضی هستند و نقطه O وسط پاره خط FF’ ، مرکز بیضی است. فرض کنید اندازه پاره خط های OA ، OB و OF را به ترتیب با a ، b و c نمایش دهیم. بنابراین فاصله دو کانون بیضی برابر 2c است.
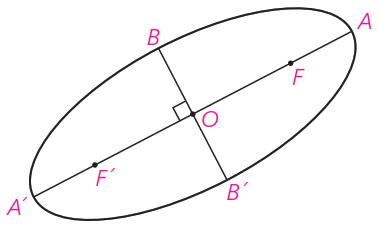
١ در ترسیم بیضی با نخ و قلم دو وضعیتی را که قلم در نقاط A و ′A قرار می گیرد درنظر بگیرید.
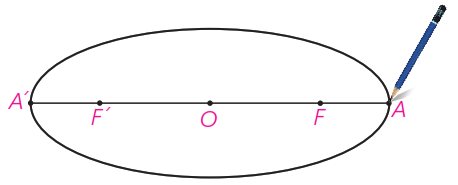
الف نشان دهید که ′FA=F′A و از آن نتیجه بگیرید OA = OA’ = a و لذا اندازه قطر بزرگ بیضی برابر 2a است.
ب نشان دهید طول نخ موردنظر برابر است با طول قطر بزرگ بیضی.
الف با توجه به قسمت اول فعالیت قبل می توان نوشت:
\(\begin{array}{l}FA + F'A = l\\\\ \Rightarrow FA + FA + FF' = l\\\\ \Rightarrow FA + FA = l - FF'\\\\ \Rightarrow 2FA = l - FF'\end{array}\)
به طریق مشابه، با در نظر گرفتن نقطه A' می توان نوشت: 2FA=1-FF' ؛ پس :
\(\begin{array}{l}FA' = F'A = \frac{1}{2}l\\\\ \Rightarrow FF' + F'A' = FF' + + FA\\\\ \Rightarrow FA = F'A'\\\\OF = OF'\\\\ \Rightarrow OF + FA = OF' + F'A'\\\\ \Rightarrow OA = O'A' = a\end{array}\)
ب
\(\begin{array}{l}AF + AF' = l\;\;\\\\\mathop \Rightarrow \limits^{AF = A'F'} \;\;A'F' + AF' = l\\\\ \Rightarrow AA' = l \Rightarrow l = 2a\end{array}\)
٢ الف در رسم بیضی وضعیتی را که قلم در نقطه B قرار دارد درنظر بگیرید و نشان دهید:
ب با انجام همین کار برای نقطه ′B نتیجه بگیرید \(OB{'^2} + {c^2} = {a^2}\)
و با توجه به آن نتیجه بگیرید OB′ = OB = b و لذا اندازه قطر کوچک بیضی برابر 2b است.
الف
ب
\(\begin{array}{l}\Delta OB'F \cong \Delta OB'F'\\\\ \Rightarrow B'F = B'F'\\\\B'F + B'F' = AA' = 2a\\\\ \Rightarrow 2BF = 2a \Rightarrow BF = a\\\\\Delta OBF:\widehat O = {90^ \circ }\\\\ \Rightarrow O{{B'}^2} + O{F^2} = B'{F^2}\\\\ \Rightarrow O{{B'}^2} + {c^2} = {a^2}\quad (2)\\\\(1)\;,\;(2) \Rightarrow O{B^2} = O{{B'}^2}\\\\ \Rightarrow OB = OB' = b\\\\ \Rightarrow {a^2} = {b^2} + {c^2}\end{array}\)
1736019749.png)
