شاه کلید نکات
شاه کلید سوال
1 دو ظرف به گنجایش 12 و 18 لیتر داریم. می خواهیم با یک پیمانه که هر بار پر و خالی می شود، دو ظرف را به طور کامل پر کنیم.کدام پیمانه ها برای این کار مناسب است؟ بزرگ ترین پیمانه کدام است؟
ابتدا تمام شمارنده های عددهای 12 و 18 را بدست می آوریم:
12 ، 6 ، 4 ، 3 ، 2 ، 1 : شمارنده های 12
18 ، 9 ، 6 ، 3 ، 2 ، 1 : شمارنده های 18
سپس شمارنده های مشترک 12 و 18 را مشخص می کنیم:
6 ، 3 ، 2 ، 1 : شمارنده های مشترک 12 و 18
پیمانه های 1 ، 2 ، 3 و 6 لیتری برای این کار مناسب هستند. برای پیدا کردن بزرگترین پیمانه، ب.م.م دو عدد 12 و 18 را پیدا می کنیم:
\((12\,,\,18) = 6\)
بنابراین بزرگترین پیمانه، پیمانۀ 6 لیتری است.
2 یک مکعب مستطیل به ابعاد 12 و 36 و 28 سانتی متر را با مکعب های مساوی پر کرده ایم. بزرگ ترین ضلع این مکعب چه عددی است؟ در این صورت چند مکعب در این مکعب مستطیل جا می شود؟
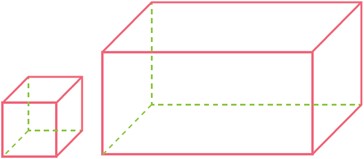
باید ب.م.م این سه عدد را بدست آوریم. برای این کار ابتدا باید تمام شمارنده های اوّل این سه عدد را بدست آوریم:
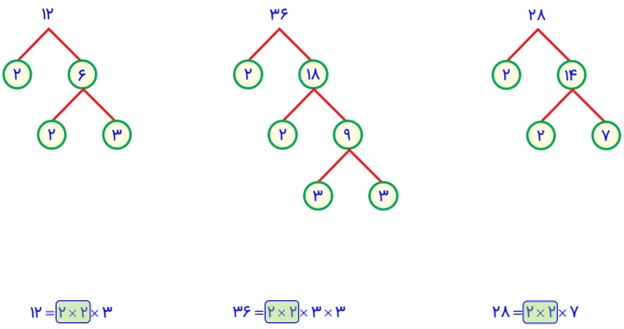
ب.م.م این سه عدد، 4 است؛ در نتیجه بزرگترین ضلع این مکعب باید 4 سانتی متر باشد:
\((12\,,\,36\,,\,28) = 2 \times 2 = 4\)
28 ، 36 ، 12 : ابعاد مکعب مستطیل
4 ، 4 ، 4 : ابعاد مکعب های کوچکتر
\( = \frac{{12 \times 36 \times 28}}{{4 \times 4 \times 4}} = \) تعداد مکعب های کوچکتر
\(\begin{array}{l}\frac{{(3 \times \not 4) \times (9 \times \not 4) \times (7 \times \not 4)}}{{\not 4 \times \not 4 \times \not 4}} = \\\\3 \times 9 \times 7 = 189\end{array}\)
بنابراین کمترین تعداد مکعبی که ای مکعب مستطیل را پر می کند، 189 عدد می باشد.
3 برای درستی جملات زیر دلیل بیاورید.
الف اگر دو عدد b و a اول باشند، ب.م.م آنها عدد یک می شود.
\((a\,,\,b) = 1\)
ب اگر عددی بر عدد دیگری بخش پذیر باشد، عدد کوچک تر ب.م.م دو عدد است.
پ کوچک ترین مقسومٌ علیه مشترک (یا شمارندهٔ مشترک) هر دو عدد 1 است.
الف
می دانیم که هر عدد اوّل (a و b) را می توان فقط به صورت حاصل ضرب خودش در عدد یک نوشت:
\(\left\{ \begin{array}{l}a = 1 \times a\\\\b = 1 \times b\end{array} \right. \Rightarrow \) شمارندۀ مشترک عدد 1 است \( \Rightarrow (a\,,\,b) = 1\)
ب
بزرگترین شمارندۀ هر عدد برابر است با خود آن عدد و وقتی آن عدد بر عدد دیگر هم بخش پذیر باشد، در نتیجه شمارندۀ آن عددِ دیگر نیز می شود و با توجه به اینکه هم شمارندۀ خودش است و هم شمارندۀ آن عدد دیگر و از خودش نیز بزرگتر در شمارنده های دو عدد وجود ندارد، در نتیجه ب.م.م دو عدد است.
توضیح مختصر:
چون عدد کوچکتر، عدد بزرگتر را میشمرد.
.
پ
هر عدد را می توانیم به صورت حاصل ضرب خودش در عدد یک نوشت؛ بنابراین:
\(\left\{ \begin{array}{l}a = 1 \times a\\\\b = 1 \times b\end{array} \right. \Rightarrow \) کوچکترین شمارندۀ مشترک دو عدد \( \Rightarrow (a\,,\,b) = 1\)
4 ابتدا عددهای صورت و مخرج را تجزیه کنید، سپس کسرها را ساده کنید.
\(\begin{array}{l}\frac{{96}}{{144}} = \\\\\frac{{35}}{{245}} = \end{array}\)
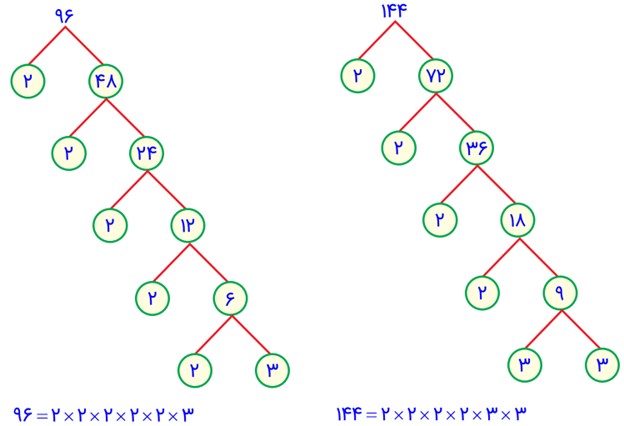
\(\frac{{96}}{{144}} = \frac{{2 \times 2 \times 2 \times 2 \times 2 \times 3}}{{2 \times 2 \times 2 \times 2 \times 3 \times 3}} = \frac{2}{3}\)
\(\frac{{35}}{{245}} = \frac{{5 \times 7}}{{5 \times 7 \times 7}} = \frac{1}{7}\)
5 ب.م.م عددهای زیر را محاسبه کنید.
\(\begin{array}{l}(91\,,\,117) = \\\\(216\,,\,108) = \\\\(121\,,\,55) = \end{array}\)
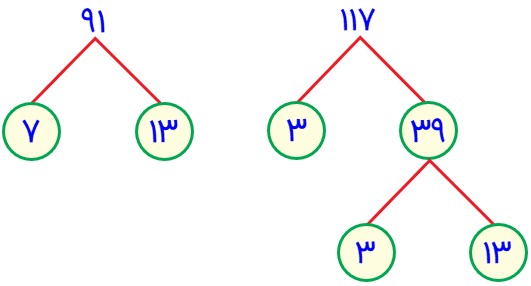
\(\left\{ \begin{array}{l}91 = 7 \times \underline {13} \\\\117 = 3 \times 3 \times \underline {13} \end{array} \right. \Rightarrow (91\,,\,117) = 13\)
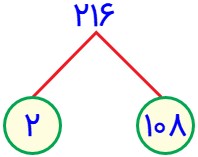
\(\left\{ \begin{array}{l}216 = 2 \times 108\\\\108 = 1 \times 108\end{array} \right. \Rightarrow (216\,,\,108) = 108\)
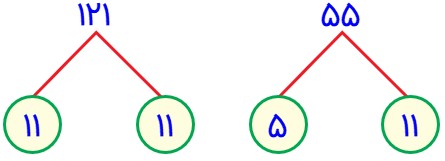
\(\left\{ \begin{array}{l}121 = 11 \times \underline {11} \\\\55 = 5 \times \underline {11} \end{array} \right. \Rightarrow (121\,,\,55) = 11\)
6 برای جملات درست زیر 2 مثال بزنید.
الف (n , n) = n
ب ب.م.م دو عدد a و b شمارندۀ دو عدد a و b است.
پ اگر عدد a اول باشد، ب.م.م a و عدد دیگر مثل b یا یک می شود یا خود a.
الف
n هر عددی می تواند باشد؛ پس:
\(\begin{array}{l}(5\,,\,5) = 5\\\\(100\,,\,100) = 100\end{array}\)
ب
\(\left\{ \begin{array}{l}a = 12 \Rightarrow 1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\\\\b = 6 \Rightarrow 1\,,\,2\,,\,3\,,\,6\end{array} \right. \Rightarrow (12\,,\,6) = 6\)
6 شمارندۀ 6 است 6 = 6 × 1
6 شمارندۀ 12 است 12 = 6 × 2
\(\left\{ \begin{array}{l}a = 20 \Rightarrow 1\,,\,2\,,\,4\,,\,5\,,\,10\,,\,20\\\\b = 10 \Rightarrow 1\,,\,2\,,\,5\,,\,10\end{array} \right. \Rightarrow (20\,,\,10) = 10\)
10 شمارندۀ 10 است 10 = 10 × 1
10 شمارندۀ 20 است 20 = 10 × 2
پ
\(\begin{array}{l}\left\{ \begin{array}{l}a = 3 \Rightarrow 1\,,\,3\\\\b = 7 \Rightarrow 1\,,\,7\end{array} \right. \Rightarrow (a\,,\,b) = (3\,,\,7) = 1\\\\\left\{ \begin{array}{l}a = 3 \Rightarrow 1\,,\,3\\\\b = 7 \Rightarrow 1\,,\,2\,,\,3\,,\,6\end{array} \right. \Rightarrow (a\,,\,b) = (3\,,\,6) = 3\end{array}\)
1736019749.png)
