جواب کاردرکلاس صفحه 56 درس 5 ریاضی هفتم (شمارنده ها و اعداد اول)
تعداد بازدید : 86.39Mپاسخ کاردرکلاس صفحه 56 ریاضی هفتم
-گام به گام کاردرکلاس صفحه 56 درس شمارنده ها و اعداد اول
-کاردرکلاس صفحه 56 درس 5
-شما در حال مشاهده جواب کاردرکلاس صفحه 56 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با یکی از روش های بالا شمارنده های هر عدد را مشخص کنید.
: شمارنده های 14
: شمارنده های 15
: شمارنده های 9
: شمارنده های 8
14 ، 7 ، 2 ، 1 : شمارنده های 14
یعنی 14 تا دستۀ یکی ای 1 × 14 = 14
یعنی 7 دستۀ 2 تایی 2 × 7 = 14
یعنی 2 دستۀ 7 تایی 7 × 2 = 14
یعنی 1 دستۀ 14 تایی 14 × 1 = 14
15 ، 5 ، 3 ، 1 : شمارنده های 15
یعنی 15 تا دستۀ یکی ای 1 × 15 = 15
یعنی 5 تا دستۀ 3 تایی 3 × 5 = 15
یعنی 3 تا دستۀ 5 تایی 5 × 3 = 15
یعنی 1 دستۀ 15 تایی 15 × 1 = 15
9 ، 3 ، 1 : شمارنده های 9
یعنی 9 تا دستۀ یکی ای 1 × 9 = 9
یعنی 3 تا دستۀ 3 تایی 3 × 3 = 9
یعنی 1 دستۀ 9 تایی 9 × 1 = 9
8 ، 4 ، 2 ، 1 : شمارنده های 8
یعنی 8 تا دستۀ یکی ای 1 × 8 = 8
یعنی 4 تا دستۀ 2 تایی 2 × 4 = 8
یعنی 2 تا دستۀ 4 تایی 4 × 2 = 8
یعنی 1 دستۀ 8 تایی 8 × 1 = 8
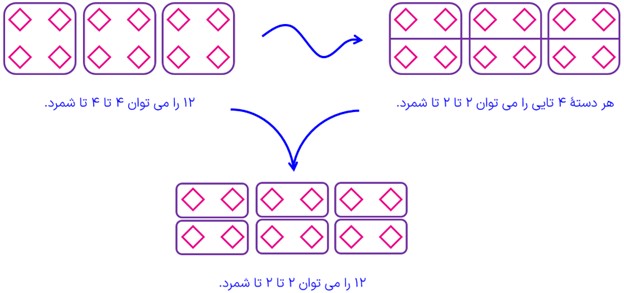
2 عدد ٢، شمارندهٔ 4 است. 4 هم شمارندهٔ 12 است. آیا می توان نتیجه گرفت که 2 شمارندهٔ 12 هم هست؟ چرا؟
بله؛ چون 12 را می توان به دسته های 4 تایی تقسیمن کرد و هر دستۀ 4 تایی را نیز می توان به دسته های 2 تایی تقسیم نمود؛ بنابراین 12 را نیز می توان به دسته های 2 تایی تقسیم نمود:
3 به طور کلی اگر a شمارندۀ b باشد، b هم شمارندۀ c باشد، آیا می توان نتیجه گرفت که a شمارندۀ c هم هست؟ چرا؟
بله؛ زیرا:
اگر a شمارندۀ b باشد، یعنی b را می توان مثلاً به m تا دستۀ a تایی تقسیم کرد:
b = m × a
و وقتی b هم شمارندۀ c باشد، یعنی c را می توان مثلاً به n تا دستۀ b تایی تقسیم کرد:
c = n × b
بنابراین:
\(\begin{array}{l}c = n \times b\\\\\mathop \Rightarrow \limits^{b = m \times a} \,\,\,\,\,c = n \times m \times a\\\\ \Rightarrow c = (n \times m) \times a\end{array}\)
یعنی c را می توان به تعداد n×m دستۀ a تایی تقسیم کرد؛ در نتیجه a شمارندۀ c نیز خواهد بود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















