دانلود اپلیکیشن
1 بین \(\sqrt 5 \) و \(\sqrt {10} \) ، چهار عدد گنگ بنویسید.
برای پیدا کردن اعداد گنگ بین \(\sqrt 5 \) و \(\sqrt {10} \) ، کافی است اعدادی بین ۵ و ۱۰ انتخاب کنیم که جذر کامل نداشته باشند و سپس جذر آنها را بنویسیم. چهار نمونه عبارتند از:
\(\sqrt 6 \,,\,\sqrt 7 \,,\,\sqrt 8 \,,\,\sqrt {9/1} \)
2 بین دو عدد 2 و 3، چهار عدد گنگ بنویسید.
ابتدا اعداد ۲ و ۳ را به صورت رادیکالی می‌نویسیم: \(2 = \sqrt 4 \) و \(3 = \sqrt 9 \) حالا باید چهار عدد گنگ بین \(\sqrt 4 \) و \(\sqrt 9 \) پیدا کنیم. چهار نمونه عبارتند از:
\(\sqrt 5 \,,\,\sqrt 6 \,,\,\sqrt 7 \,,\,\sqrt 8 \)
3 الف مجموعۀ A به صورت \(A = \left\{ {x \subseteq Q|2 \le x \le 3} \right\}\) را در نظر بگیرید. آیا نمایش A به صورت زیر درست است؟
ب نقطهٔ نمایش \(\sqrt 5 \) را روی محور مشخص کنید.
الف
خیر، نمایش داده شده درست نیست.
دلیل: مجموعهٔ \(A = \left\{ {x \subseteq Q|2 \le x \le 3} \right\}\) شامل تمام اعداد گویا بین ۲ و ۳ است. اما خط ممتد و توپر روی محور، نمایش‌دهندهٔ تمام اعداد حقیقی (شامل گویا و گنگ) بین ۲ و ۳ است. از آنجایی که بین ۲ و ۳ اعداد گنگ بی‌شماری مانند \( \cdots \,,\,\sqrt 6 \,,\,\sqrt 5 \) وجود دارند که در مجموعه A نیستند، این نمایش صحیح نمی‌باشد.
ب
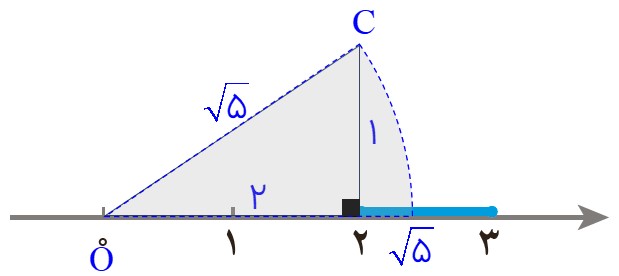
برای مشخص کردن \(\sqrt 5 \) روی محور، از قضیه فیثاغورس استفاده می‌کنیم:
1 یک مثلث قائم‌الزاویه روی محور اعداد رسم می‌کنیم که یک ضلع آن به طول ۲ واحد (از ۰ تا ۲) و ضلع دیگر آن به طول ۱ واحد (عمود بر محور) باشد.
2 طول وتر این مثلث برابر با \(\sqrt {{2^2} + {1^2}} = \sqrt {4 + 1} = \sqrt 5 \) خواهد بود.
3 با استفاده از پرگار، دهانه را به اندازه طول وتر باز کرده، سوزن آن را روی مبدأ (نقطه ۰) قرار می‌دهیم و یک کمان می‌زنیم تا محور اعداد را قطع کند. نقطهٔ برخورد، نمایش عدد \(\sqrt 5 \) است.
1736019749.png)
