جواب تمرین صفحه 10 درس 1 ریاضی و آمار دوازدهم انسانی (آمار و احتمال)

10 + 11 + 12 = 33

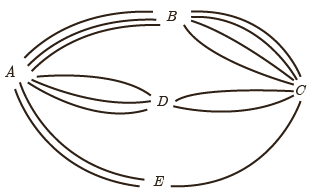
الف 

\(\left( {3 \times 4} \right) + \left( {3 \times 2} \right) + \left( {2 \times 1} \right) = 20\)

ب 

\(\left( {3 \times 4} \right) + \left( {4 \times 3} \right) = 24\)

پ 

\(3 + \left( {2 \times 3 \times 4} \right) = 27\)

الف 

\(5 \times 4 \times 3 \times 2 \times 1 = 5! = 120\)

ب 

\(4 \times 3 \times 1 = 12\)

پ 

\(1 \times 3 \times 2 \times 1 \times 1 = 6\)

\(p(10\;,\;2) = \frac{{10!}}{{8!}} = 90\)

\(7 \times 2 \times 3 = 42\)

الف 

\(5 \times 4 \times 3 \times 2 \times 4 = 480\)

ب 

\(2 \times 5 \times 4 \times 3 \times 2 = 240\)

پ 

\(\left( {\begin{array}{*{20}{c}}6\\3\end{array}} \right) = 20\)

ت کافی است تعداد زیرمجموعه های دو عضوی مجموعه {1,2,4,6,9} را پیدا کنیم:

\(\left( {\begin{array}{*{20}{c}}{6 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) = 10\)

الف 

\(\left( {\begin{array}{*{20}{c}}{12}\\3\end{array}} \right) = 220\)

ب 

\(\left( {\begin{array}{*{20}{c}}{12}\\2\end{array}} \right) = 66\)

الف 

\(\left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\3\end{array}} \right) = 10 \times 20 = 200\)

ب چون از 6 نفر تیم والیبال یک نفر مشخص شده است که کاپیتان است، پس باید دنبال 5 نفر دیگر بگردیم که در نقش های دیگر تیم قرار بگیرند؛ همچنین چون از 6 نفر کلاس دوازدهم انتخاب کرده ایم، یک نفر از آنان کم می شود و در  کل از 11 نفر موجود یک نفر کم می شود؛ پس بایستی از 10 نفر باقی مانده، 5 نفر را برای پست های باقی مانده در تیم انتخاب کنیم:

\(\left( {\begin{array}{*{20}{c}}{11 - 1}\\{6 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}\\5\end{array}} \right) = 252\)

پ 

\(\begin{array}{l}\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\4\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\5\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\0\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\6\end{array}} \right)\\\\ = (10 \times 15) + (5 \times 6) + (1 \times 1)\\\\ = 150 + 30 + 1 = 181\end{array}\)

ت 

\(\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}6\\4\end{array}} \right) = 10 \times 15 = 150\)

با توجه به شکل زیر، تعداد مسیرهای سفر از شهر A به شهر B را بدست آورید.

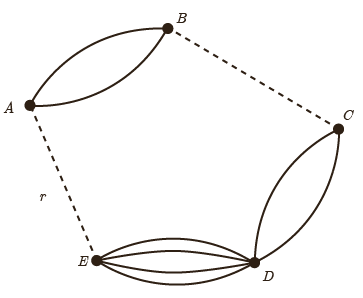
طبق شکل، تعداد را های از A به D از رابطه زیر محاسبه می شود:

\(\begin{array}{l}r \times 4 + 2 \times s \times 2 = 20 \Rightarrow 4r + 4s = 20\\\\ \Rightarrow 4(r + s) = 20 \Rightarrow r + s = 5\end{array}\)

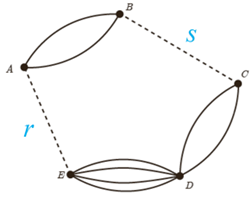
حال r و s طوری می توانند تعیین شوند که از رابطه بالا یعنی \(r + s = 5\) تبعیت کنند. می توانند مقادیر زیر باشند:

\(r + s = 5 \Rightarrow \left\{ \begin{array}{l}r = 1\quad ,\quad s = 4\\r = 2\quad ,\quad s = 3\\r = 3\quad ,\quad s = 2\\r = 4\quad ,\quad s = 1\end{array} \right.\)