جواب تمرین صفحه 25 درس 1 ریاضی و آمار دوازدهم انسانی (آمار و احتمال)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 25 ریاضی و آمار دوازدهم انسانی
-گام به گام تمرین صفحه 25 درس آمار و احتمال
-تمرین صفحه 25 درس 1
-شما در حال مشاهده جواب تمرین صفحه 25 ریاضی و آمار دوازدهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 کدام یک از پدیده های زیر آزمایش تصادفی و کدام یک آزمایش قطعی است؟
الف نام 20 دانش آموز را روی 20 کارت می نویسیم و پس از مخلوط کردن کارت ها، به طور تصادفی یک کارت بیرون می کشیم تا نام یکی از دانش آموزها استخراج شود.
ب مقداری آب را حرارت می دهیم تا به بخار تبدیل شود.
پ نتیجهٔ یک آزمون چهارجوابی، که نیمی از سؤالات آن را شانسی پاسخ داده ایم.
ت در یک بازی سادهٔ دو نفره، یکی از دو نفر مراحل زیر را انجام می دهد.
- عددی را انتخاب می کند.
- سه واحد به آن عدد می افزاید.
- سپس حاصل را دو برابر می کند.
- از عدد حاصل 2 واحد کم می کند.
- نتیجهٔ به دست آمده را نصف می کند.
- از حاصل به دست آمده، عدد اوّلیه را کم می کند.
- در مرحلهٔ آخر، فرد دوم به جای شخص محاسبه کننده پاسخ را اعلام می کند.
الف تصادفی
ب قطعی
پ تصادفی
ت نتیجه همواره 2 است؛ بنابراین قطعی
2 سکه ای را پرتاب می کنیم. اگر رو ظاهر شد، آن گاه تاس را می ریزیم. در غیر این صورت، یک بار دیگر سکه را می اندازیم.
الف فضای نمونهٔ این آزمایش تصادفی را مشخص کنید.
ب پیشامد A را که در آن عدد ظاهر شده روی تاس زوج باشد یا سکه پشت بیاید، با اعضا مشخص کنید.
الف
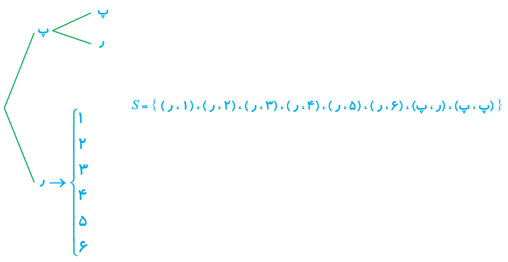
ب
{ (پ،پ) ، (ر،پ) ، (6،ر) ، (4،ر) ، (2،ر) } = A
3 هر یک از اعداد فرد طبیعی کوچک تر از 20 را روی یک کارت می نویسیم و پس از مخلوط کردن کارت ها به طور تصادفی یک کارت را برمی داریم؛ مطلوب است تعیین:
الف فضای نمونهٔ این آزمایش تصادفی
ب پیشامد A که در آن عدد روی کارت مضرب 3 باشد.
پ پیشامد B که در آن عدد روی کارت، مجذور کامل باشد.
ت پیشامدهای \(A \cap B\) و \(A - B\) را با اعضا مشخص کنید.
الف
\(S = \left\{ {1\;,\;3\;,\;5\;,\;7\;,\;9\;,\;11\;,\;13\;,\;15\;,\;17\;,\;19} \right\}\)
ب
\(A = \left\{ {3\;,\;9\;,\;15} \right\}\)
پ
\(B = \left\{ {1\;,\;9} \right\}\)
ت
\(\begin{array}{l}A \cap B = \left\{ {1\;,\;9} \right\}\\\\A - B = \left\{ {3\;,\;15} \right\}\end{array}\)
4 برای هر یک از پیشامدهای زیر یک عبارت توصیفی و یک عبارت مجموعه ای بنویسید.
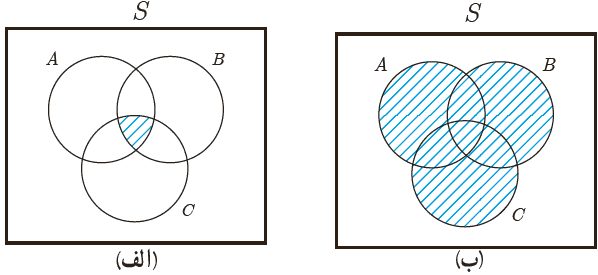
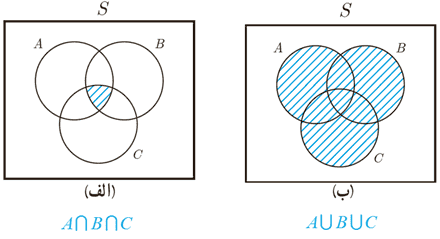
5 هر یک از اعداد دو رقمی را که با ارقام 4، 3، 2، 1 می توان نوشت، روی کارت هایی می نویسیم و پس از مخلوط کردن کارت ها یک کارت را به طور تصادفی خارج می کنیم. الف فضای نمونهٔ این آزمایش تصادفی را مشخص کنید.
ب پیشامد A که در آن عدد روی کارت مضرب 6 باشد. پ پیشامد B که در آن عدد روی کارت اوّل باشد.
الف
\(S = \left\{ \begin{array}{l}11\;,\;12\;,\;13\;,\;14\;,\;21\;,\;22\;,\\23\;,\;24\;,\;31\;,\;32\;,\;33\;,\\34\;,\;41\;,\;42\;,\;43\;,\;44\end{array} \right\}\)
ب
\(A = \left\{ {12\;,\;24\;,\;42} \right\}\)
پ
\(B = \left\{ {11\;,\;13\;,\;23\;,\;31\;,\;41\;,\;43} \right\}\)
6 خانواده ای دارای 3 فرزند است.
الف فضای نمونهٔ مناسب برای ترکیب جنسیت فرزندان این خانواده چیست؟
ب پیشامد A که در آن هر سه فرزند از یک جنس باشند.
پ پیشامد B که در آن فقط یک فرزند دختر باشد.
ت پیشامد C که در آن حداقل 2 فرزند پسر باشند.
ث پیشامد D که در آن حداکثر یک فرزند پسر باشد.
الف
، ( د ، پ ، د ) ، ( پ ، پ ، د ) ، ( د، د ، پ ) ، ( پ ، د ، پ ) ، ( د ، پ ، پ ) ، ( پ ، پ ، پ ) } = S
{ ( د ، د ، د ) ، ( پ ، د ، د )
ب
{ ( د ، د ، د ) ، ( پ ، پ ، پ ) } = A
{ ( د ، د ، د ) ، ( پ ، پ ، پ ) } = A
پ
{ ( پ ، پ ، د ) ، ( پ ، د ، پ ) ، ( د ، پ ، پ ) } = B
ت
{ ( پ ، پ ، د ) ، ( پ ، د ، پ ) ، ( د ، پ ، پ ) ، ( پ ، پ ، پ ) } = C
ث
{ ( د ، د ، د ) ، ( پ ، د ، د ) ، ( د ، پ ، د ) ، ( د، د ، پ ) } = S
7 خانواده ای دارای 4 فرزند است.
الف فضای نمونه مناسب برای ترکیب جنسیت فرزندان این خانواده چند عضو دارد؟
ب پیشامد A را مشخص کنید؛ طوری که در آن دو فرزند سوم و چهارم دختر باشند.
پ پیشامد C که در آن تعداد فرزندان دختر بیشتر از تعداد فرزندان پسر باشد.
ت آیا پیشامدهای A و C ناسازگارند؟
الف
\(n(S) = {2^4} = 16\)
ب
{ ( د ، د ، د ، د) ، ( د ، د ، پ ، د) ، ( د ، د ، د ، پ) ، (د ، د ، پ ، پ ) } = A
پ
{ ( د ، د ، د ، د) ، ( پ ، د ، د ، د) ، ( د ، پ ، د ، د) ، ( د ، د ، پ ، د) ، (د ، د ، د ، پ ) } = C
ت خیر؛ ناسازگار نیستند.
8 از جعبه ای که شامل 12 سیب سالم و 5 سیب لکه دار است، 3 سیب را به طور تصادفی برمی داریم. مطلوب است محاسبهٔ احتمال اینکه:
الف هر سه سیب سالم باشند.
ب دو سیب سالم و یک سیب لکه دار باشد.
پ تعداد سیب های سالم از تعداد سیب های لکه دار بیشتر باشد.
الف
\(P(A) = \frac{{\left( {\begin{array}{*{20}{c}}{12}\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\0\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{17}\\3\end{array}} \right)}} = \frac{{220 \times 1}}{{680}} = \frac{{11}}{{34}}\)
ب
\(P(B) = \frac{{\left( {\begin{array}{*{20}{c}}{12}\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{17}\\3\end{array}} \right)}} = \frac{{66 \times 5}}{{680}} = \frac{{33}}{{68}}\)
پ
\(\begin{array}{l}P(C) = \frac{{\left( {\begin{array}{*{20}{c}}{12}\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\0\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{12}\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{17}\\3\end{array}} \right)}}\\\\ = \frac{{11}}{{34}} + \frac{{33}}{{68}} = \frac{{55}}{{68}}\end{array}\)
9 عقربهٔ دستگاه چرخندهٔ زیر، پس از به حرکت درآمدن روی یکی از 8 ناحیه می ایستد و عددی را نشان می دهد. چقدر احتمال دارد که:
الف عقربه روی یک عدد اوّل بایستد.
ب عقربه یک عدد اوّل یا فرد را نشان دهد.
پ عقربه روی یک عدد مضرب 3 بایستد.
الف
\(\begin{array}{l}S = \left\{ {1\;,\;2\;,\;3\;,\;4\;,\;5\;,\;6\;,\;7\;,\;8} \right\}\\\\A = \left\{ {2\;,\;3\;,\;5\;,\;7} \right\} \to P(A) = \frac{4}{8} = \frac{1}{2}\end{array}\)
ب
\(B = \left\{ {1\;,\;2\;,\;3\;,\;5\;,\;7} \right\} \to P(B) = \frac{5}{8}\)
پ
\(C = \left\{ {3\;,\;6} \right\} \to P(B) = \frac{2}{8} = \frac{1}{4}\)
10- 7 پرچم مختلف را به هفت میلهٔ پرچم نصب کرده ایم و روی میله ها شماره های 1 تا 7 را حک کرده ایم. چنانچه این پرچم ها به طور تصادفی کنار هم قرار گیرند، مطلوب است محاسبهٔ احتمال اینکه میلهٔ پرچم ها با شماره های غیر اوّل در مکان های زوج باشند.
پرچم های اول: 2 ، 3 ، 5 ، 7 (در رابطه زیر به رنگ قرمز)
پرچم های غیر اول: 1 ، 4 ، 6 (در رابطه زیر به رنگ بنفش)

تعداد کل حالت ها : \(7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 5040\)
\(P\left( E \right) = \frac{{144}}{{5040}} = \frac{1}{{35}}\)
11 یازده بازیکن فوتبال تیم مدرسهٔ شما به طور تصادفی کنار یکدیگر قرار می گیرند تا عکسی یادگاری بیندازند. چنانچه دروازه بان و کاپیتان تیم دو نفر متفاوت باشند، مطلوب است محاسبهٔ احتمال اینکه در عکس دقیقاً 4 نفر بین دروازه بان و کاپیتان حضور داشته باشند؟

توضیح:
بایستی مابین دروازه بان و کاپیتان 4 نفر باشند، همچنین می دانیم می توان جایگاه دروازه بان را به سمت چپ انتقال داد؛ در نتیجه طبق خواسته مسأله به ازای انتقال دروازه بان به سمت چپ، کاپیتان نیز به سمت چپ منتقل می شود که در این مورد، 6 حالت داریم؛ همچنین می توان جای دروازه بان و کاپیتان را نیز جابجا کرد که در این مورد ، 2 حالت دیگر داریم؛ در مجموع تعداد حالت های کل برای خواسته مسأله داریم :
تعداد حالت های مساعد : \(9!\; \times 6 \times 2 = 9!\; \times 12\)
: تعداد حالت های کل 11!
\(P(E) = \frac{{9!\: \times 12}}{{11\:!}} = \frac{{12}}{{11 \times 10}} = \frac{6}{{55}}\)
12 در یک پارک جنگلی حفاظت شده، 20 قوچ وحشی البرز مرکزی وجود دارد؛ 5 تا از آنها را می گیرند و پس از نشان دار کردن، رهایشان می کنند. بعد از مدتی، محیط بانان به طور تصادفی 7 تا از آنها را می گیرند و می خواهند تعداد قوچ های نشان دار را بشمارند. مطلوب است محاسبهٔ احتمال اینکه حداکثر 2 قوچ نشانه دار باشند.
\(\begin{array}{l}P(E) = \frac{{\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}{15}\\5\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}{15}\\6\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\0\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}{15}\\7\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{20}\\7\end{array}} \right)}}\\\\ = \frac{{10 \times 3003 + 5 \times 5005 + 1 \times 6435}}{{77520}}\\\\ = \frac{{61490}}{{77520}} \simeq 0/79\end{array}\)
13 انجمن اولیا و مربیان یک دبیرستان 10 نفر عضو دارد. به یک برنامهٔ خاص، 5 نفر رأی موافق، 3 نفر رأی مخالف و 2 نفر رأی ممتنع داده اند. از بین آنها به طور تصادفی 3 نفر انتخاب می کنیم. مطلوب است محاسبهٔ احتمال اینکه:
الف حداقل 2 نفر از افراد انتخابی موافق برنامه باشند.
ب نظر هیچ دو نفری از آنها مانند هم نباشد.
الف
\(\begin{array}{l}P(A) = \frac{{\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right) + \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\0\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right)}}\\\\ = \frac{{10 \times 5 + 10 \times 1}}{{120}} = \frac{{60}}{{120}} = \frac{1}{2}\end{array}\)
ب
\(\begin{array}{l}P(B) = \frac{{\left( {\begin{array}{*{20}{c}}5\\1\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}2\\1\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right)}}\\\\ = \frac{{5 \times 3 \times 2}}{{120}} = \frac{{30}}{{120}} = \frac{1}{4}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















