جواب تمرین صفحه 108 درس 4 حسابان دوازدهم (مشتق)
تعداد بازدید : 86.34Mپاسخ تمرین صفحه 108 حسابان دوازدهم
-گام به گام تمرین صفحه 108 درس مشتق
-تمرین صفحه 108 درس 4
-شما در حال مشاهده جواب تمرین صفحه 108 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 جدول زیر درجه حرارت T (سانتی گراد) را در شهری از ساعت 8 تا 18 در یک روز نشان می دهد.

آهنگ تغییر متوسط درجه حرارت نسبت به زمان را:
الف از ساعت 8 تا ساعت 12 به دست آورید.
ب از ساعت 12 تا ساعت 18 به دست آورید.
پ پاسخ ها را تفسیر کنید.
الف
\(\frac{{T(12) - T(8)}}{{12 - 8}} = \frac{{19 - 11}}{4} = 2\)
ب
\(\frac{{T(18) - T(12)}}{{18 - 12}} = \frac{{9 - 19}}{6} = - \frac{5}{3}\)
پ
در بازه ی زمانی ساعت 8 تا ساعت 12 ظهر، درجه حرارت با آهنگ 2 درجه سانتی گراد در ساعت در حال افزایش است. اما در بازه ی زمانی ساعت 12 ظهر تا ساعت 18 درجه حرارت با آهنگ \( - \;\frac{5}{3}\) درجه سانتی گراد در ساعت در حال کاهش است.
2 کسری از جمعیت یک شهر که به وسیله یک ویروس آلوده شده اند برحسب زمان (هفته) در نمودار روبه رو نشان داده شده است.
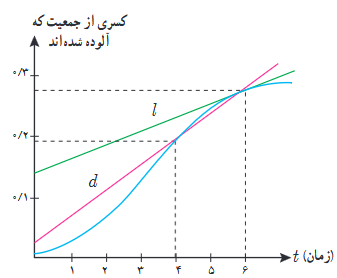
الف شیب خطوط l و d چه چیز هایی را نشان می دهند.
ب گسترش آلودگی در کدام یک از زمان های t=2 ، t=1 یا t=3 بیشتر است؟
پ قسمت ب را برای t=5 ، t=4 و t=6 بررسی کنید.
الف
شیب خطl ، آهنگ تغییر لحظه ای کسری از جمعیت آلوده شده در لحظۀ t=6 (هفتۀ ششم) نشان می دهد.
شیب خطd ، آهنگ تغییر متوسط کسری از جمعیت آلوده شده در فاصلۀ زمانیt=4 تا t=6 (هفتۀ چهارم تا هفتۀ ششم) نشان می دهد.
ب
در t=3 (هفتۀ سوم).
پ
در t=4 (هفتۀ چهارم).
3 نمودار روبه رو نمایش میزان فروش تعداد نوعی کالا (N) پس از صرف t میلیون تومان هزینه برای تبلیغ است.
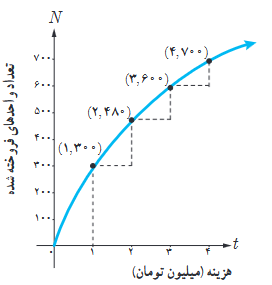
الف آهنگ تغییر N برحسب t را وقتی t از 0 تا 1، 1 تا 2 ، 2 تا 3 و 3 تا 4 تغییر می کند به دست آورید.
ب به نظر شما چرا آهنگ تغییرات، وقتی که مقادیر t افزایش می یابند، در حال کاهش است؟
الف
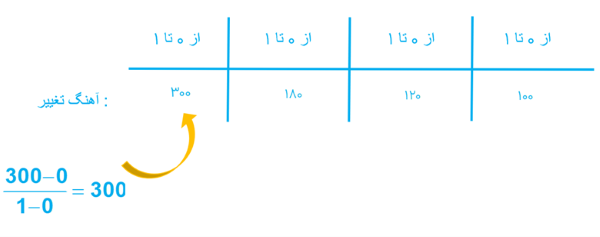
ب
زیرا با افزایش هزینه، تعداد کالاهای فروخته شده کم می شود، و رشد کمتری دارد. در نتیجه خریداران کم می شوند.
4 معادله حرکت متحرکی به صورت \(f\left( t \right) = {t^2} - t + 10\) برحسب متر در بازه زمانی [0,5] (t بر حسب ثانیه) داده شده است. در کدام لحظه سرعت لحظه ای با سرعت متوسط در بازهٔ زمانی [0,5] با هم برابرند؟
\( = \frac{{f(5) - f(0)}}{{5 - 0}} = \frac{{30 - 10}}{5} = 4m/s\) سرعت متوسط
\( = 2t - 1 \Rightarrow 2t - 1 = 4 \Rightarrow t = 2/5\;s\) سرعت لحظه ای
5 توپی از یک پل به ارتفاع 11 متر به هوا پرتاب می شود. F(t) نشان دهنده فاصله توپ از سطح زمین در زمان t است. برخی از مقادیر f(t) در جدول زیر نمایش داده شده است.

بر اساس جدول کدام یک از مقادیر زیر می تواند سرعت توپ را هنگامی که در ارتفاع نظیر زمان 0/4 ثانیه است، نشان دهد؟
\(1/23 m/s\) الف
\(12/91 m/s\) ب
\(11/5 m/s\) پ
\(16/03 m/s\) ت
\(\left\{ \begin{array}{l}\frac{{f(0/4) - f(0/3)}}{{0/1}} = 12\;m/s\\\frac{{f(0/5) - f(0/4)}}{{0/1}} = 11\;m/s\end{array} \right. \Rightarrow f'(0/4) = \frac{{12 + 11}}{2} = 11/5\;m/s\)
لذا گزینه (ج) جواب صحیح است.
6 کدام یک از عبارات زیر درست و کدام یک نادرست است:
الف آهنگ تغییر متوسط تابعی مانند f در بازه [0,1] همیشه کمتر از شیب آن منحنی در نقطه است.
ب اگر تابعی صعودی باشد، آهنگ تغییر متوسط آن، همواره صعودی است.
پ تابعی وجود ندارد که برای آن هم f’(a)=0 و هم f(a)=0
الف
نادرست
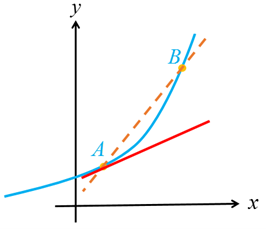
ب
نادرست

پ
نادرست؛ مثلاً
\(\left\{ \begin{array}{l}y = f(x) = {(x - 1)^2}\\a = 1\end{array} \right. \Rightarrow f'(x) = 2(x - 1) \Rightarrow f(a) = f'(a) = 0\)
7 یک توده باکتری پس از t ساعت دارای جرم \(m\left( t \right) = \sqrt t + 2{t^3}\) گرم است.
الف جرم این توده باکتری در بازه زمانی \(3 \le t \le 4\) چند گرم افزایش می یابد؟
ب آهنگ رشد جرم توده باکتری در لحظه t=3 چقدر است؟
الف
\(\frac{{m(4) - m(3)}}{{4 - 3}} = \frac{{130 - \sqrt 3 - 54}}{1} \simeq 74\;g\)
ب
\(m'(t) = \frac{1}{{2\sqrt t }} + 6{t^2} \Rightarrow m'(3) = \frac{1}{{2\sqrt 3 }} + 6{(3)^2} \simeq 54/3\;g\)
8 گنجایش ظرفی 40 لیتر مایع است. در لحظهٔ t=0 سوراخی در ظرف ایجاد می شود. اگر حجم مایع باقی مانده در ظرف پس از t ثانیه از رابطه \(V = 40{\left( {1 - \frac{t}{{100}}} \right)^2}\) به دست آید:
الف آهنگ تغییر متوسط حجم مایع در بازه زمانی [0,1] چقدر است؟
ب در چه زمانی، آهنگ تغییر لحظه ای حجم برابر آهنگ تغییر متوسط آن در بازه [0,100] می شود؟
الف
لیتر \(\frac{{V(1) - V(0)}}{{1 - 0}} = 39/204 - 40 = - 0/796\)
ب
\(\left. \begin{array}{l}\frac{{V(100) - V(0)}}{{100 - 0}} = - 0/4\\V'(t) = - 0/8(1 - \frac{t}{{100}})\end{array} \right\} \Rightarrow - 0/8(1 - \frac{t}{{100}}) = - 0/4 \to 1 - \frac{t}{{100}} = \frac{1}{2} \Rightarrow t = 50\;s\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















