دانلود اپلیکیشن
1 برای هر عدد رادیکالی زیر، اگر حاصل آن یک عدد صحیح است، جواب را بنویسید و در غیر این صورت دو عدد صحیح متوالی بنویسید که عدد رادیکالی مورد نظر بین آنها باشد.
\(\begin{array}{l}\sqrt {16} \\\\\sqrt {20} \\\\\sqrt[4]{{400}}\\\\\sqrt {75} \\\\\sqrt[3]{{ - 10}}\\\\\sqrt[5]{{400}}\\\\\sqrt[3]{{ - 90}}\\\\\sqrt[3]{{250}}\\\\\sqrt[5]{1}\\\\\sqrt[3]{{20}}\end{array}\)
\(\begin{array}{l}\sqrt {16} = 4\\\\4 < \sqrt {20} < 5\\\\4 < \sqrt[4]{{400}} < 5\\\\8 < \sqrt {75} < 9\\\\\sqrt[3]{{ - 8}} = - 2\\\\3 < \sqrt[5]{{400}} < 4\\\\ - 5 < \sqrt[3]{{ - 90}} < - 4\\\\6 < \sqrt[3]{{250}} < 7\\\\\sqrt[5]{1} = 1\\\\ - 3 < - \sqrt[4]{{20}} < - 2\end{array}\)
2 مقدار تقریبی هر کدام از اعداد رادیکالی زیر را با یک رقم اعشار مشخص کنید (می توانید از ماشین حساب استفاده کنید).
\(\begin{array}{l}\sqrt {10} \\\\\sqrt[3]{{7/25}}\\\\\sqrt[5]{{16}}\\\\\sqrt[5]{{64}}\end{array}\)
\(\begin{array}{l}\sqrt {10} \simeq 3/1\\\\\sqrt[3]{{7/25}} \simeq 1/9\\\\\sqrt[5]{{16}} \simeq 1/7\\\\\sqrt[5]{{64}} \simeq 2/2\end{array}\)
3 مانند نمونه در شکل زیر، هر یک از نقاط مشخص شده روی محور بالا را به یکی از نقاط مشخص شده روی محور پایین که متناظر با ریشهٔ سوم آن عدد است، وصل کنید (یک مثال عددی از هر مورد ارائه کنید).
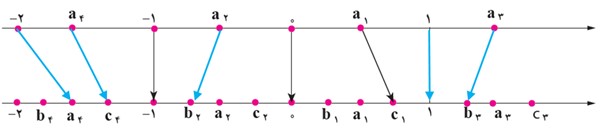
4 با توجه به آنچه دربارهٔ ریشهٔ سوم اعداد درک کرده اید، به سؤال های زیر پاسخ دهید.
الف a عددی مثبت است و \(\sqrt[3]{a} > a\) . a چه عددی می تواند باشد؟
ب a عددی است که ریشهٔ سوم آن با خودش برابر است؛ یعنی \(\sqrt[3]{a} = a\) . a چه اعدادی می تواند باشد؟
پ a عددی مثبت است و \(\sqrt[3]{a} < a\) . a چه اعدادی می تواند باشد؟
ت به موارد (الف) و (پ) برای حالتی که a عددی منفی باشد، نیز پاسخ دهید.
الف
می تواند هر عددی بین 0 و 1 باشد : 0<a<1
ب
a= -1 , 0 , 1
پ
حتماً باید عددی بزرگتر از 1 باشد: a>1
ت
برای مورد (الف) باید عددی کوچکتر از 1- باشد : a<-1
برای مورد (پ) باید عددی بین 0 و1- باشد : -1<a<0
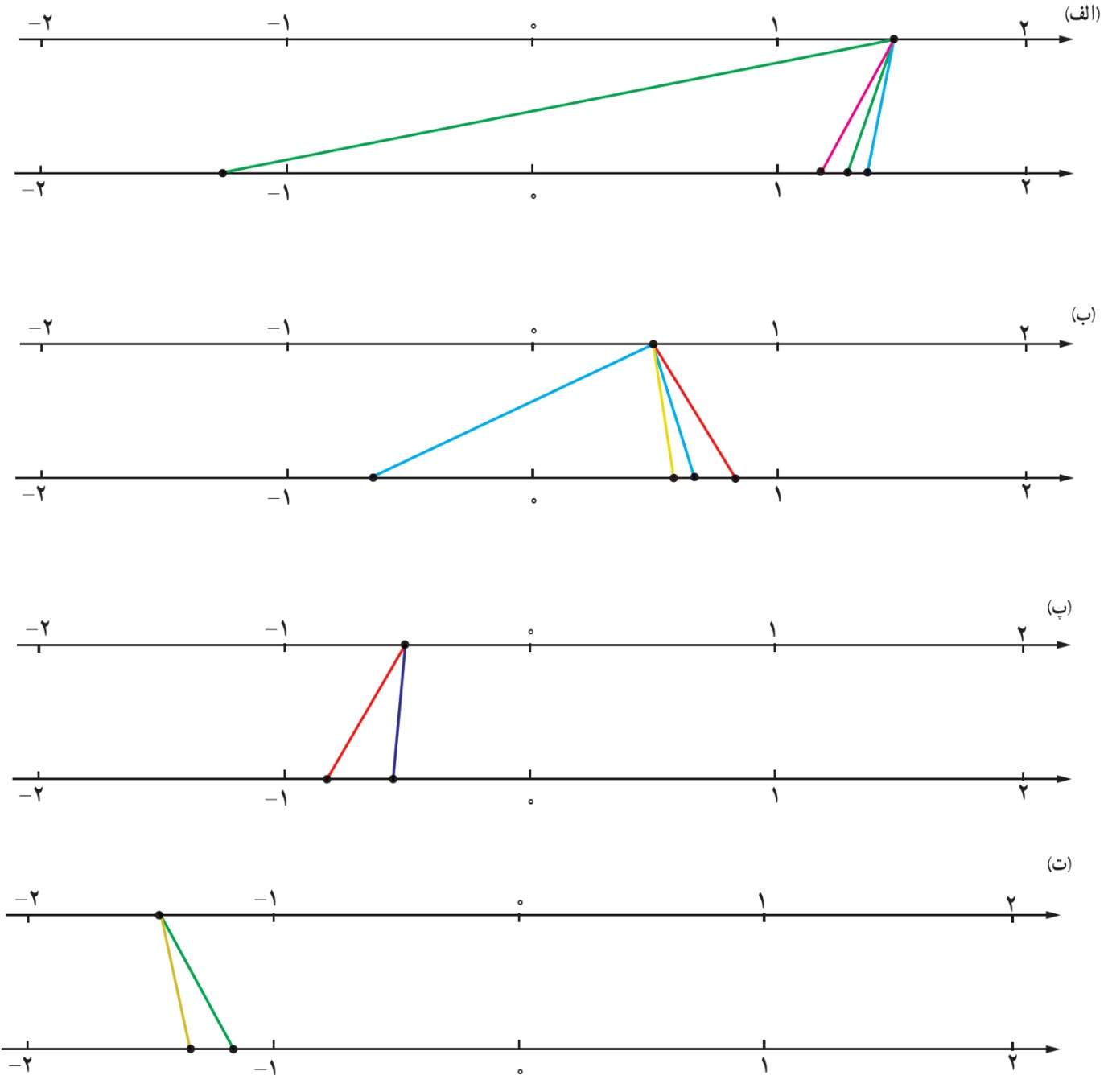
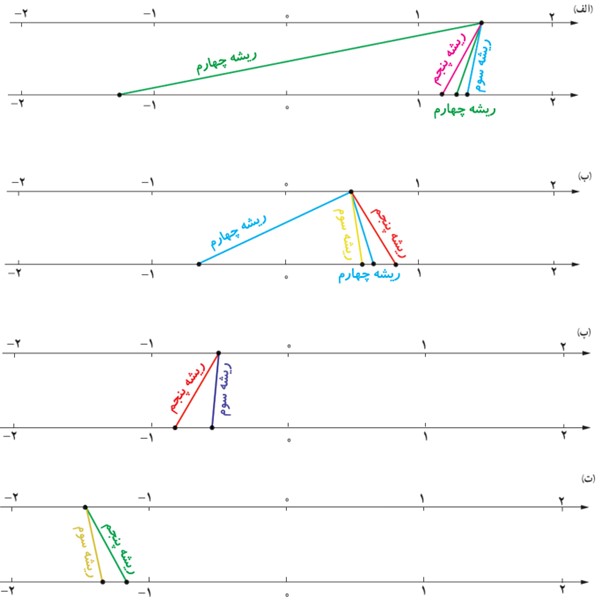
5 در هر یک از شکل های زیر، نقطه ای از محور بالا به ریشه های سوم، چهارم و پنجم خود وصل شده است. مشخص کنید هر رنگ مربوط به کدام ریشه است.
6 جاهای خالی را پر کنید.
الف اعداد 3 و ......... ریشه های چهارم عدد ......... می باشند.
ب اگر \(\sqrt[4]{{16}} = a\) باشد، در این صورت حاصل عبارت a3+5 برابر است با ………. .
الف
3- - 81
ب
13
7 در جاهای خالی یکی از علامت های « < » ، « > » یا « = » را قرار دهید.
\(\begin{array}{l}{\left( { - 0/1} \right)^5}\;\;.....\;\;{\left( { - 0/1} \right)^3}\\\\{\left( {0/1} \right)^5}\;\;.....\;\;{\left( {0/1} \right)^3}\\\\{\left( { - 2} \right)^5}\;\;.....\;\;{\left( { - 2} \right)^4}\\\\\sqrt[5]{{0/00001}}\;\;.....\;\;0/1\end{array}\)
\(\begin{array}{l}{\left( { - 0/1} \right)^5}\;\; > \;\;{\left( { - 0/1} \right)^3}\\\\{\left( {0/1} \right)^5}\;\; < \;\;{\left( {0/1} \right)^3}\\\\{\left( { - 2} \right)^5}\;\; < \;\;{\left( { - 2} \right)^4}\\\\\sqrt[5]{{0/00001}}\;\; = \;\;0/1\end{array}\)
1736019749.png)
