آیا تمام سوالات مثال صفحه 39 ریاضی دهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به مثال صفحه 39 ریاضی دهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب مثال صفحه 39 درس 2 ریاضی دهم (مثلثات)

تعداد بازدید : 78.76M

پاسخ مثال صفحه 39 ریاضی دهم

گام به گام مثال صفحه 39 درس مثلثات

مثال صفحه 39 درس 2

شما در حال مشاهده جواب مثال صفحه 39 ریاضی دهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

آقای جلالی، از دانش آموزان پرسید: اگر θ زاویه ای در ربع دوم مثلثاتی باشد و \(\sin \theta = \frac{5}{7}\)، آیا می توان سایر نسبت های مثلثاتی θ را پیدا کرد؟

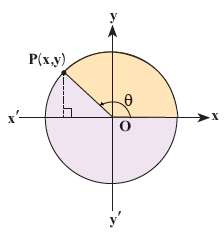
امین: می دانیم \(\sin \theta = y = \frac{5}{7}\)، بنابراین P نقطه ای به عرض ……… است.

معلم: درست است و حالا طول نقطه P چگونه به دست می آید؟

امیرعلی: طبق رابطهٔ فیثاغورس، در مثلث قائم الزاویه داریم: x²+y²=1، بنابراین ……… و در نتیجه \({x^2} = \frac{{24}}{{49}}\) پس داریم x= …….. .

معلم: آفرین، این راه کاملاً درست است، ولی کدام مقدار قابل قبول است؟

محمد مهدی: چون θ زاویه ای در ربع ……… است، پس طول نقطهٔ P منفی است و از این رو x=…….. قابل قبول است.

معلم: استدلال محمدمهدی کاملاً منطقی است و P نقطه ای به مختصات (....... و .......) است. در نتیجه:

\(\begin{array}{l}\cot \theta = \frac{{{\mkern 1mu} ...{\mkern 1mu} }}{{{\mkern 1mu} ...{\mkern 1mu} }} = \frac{{{\mkern 1mu} .....{\mkern 1mu} }}{{{\mkern 1mu} .....{\mkern 1mu} }}{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \\\\\tan \theta = \frac{y}{x} = \frac{{{\mkern 1mu} .....{\mkern 1mu} }}{{{\mkern 1mu} .....{\mkern 1mu} }}{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \\\\\cos \theta = x = .......\end{array}\)

امین: می دانیم \(\sin \theta = y = \frac{5}{7}\)، بنابراین P نقطه ای به عرض …\(\frac{5}{7}\)… است.

معلم: درست است و حالا طول نقطه P چگونه به دست می آید؟

امیرعلی: طبق رابطهٔ فیثاغورس، در مثلث قائم الزاویه داریم: x²+y²=1، بنابراین …\({x^2} + \frac{{25}}{{49}} = 1\)… و در نتیجه \({x^2} = \frac{{24}}{{49}}\) پس داریم x= …\( \pm \frac{{\sqrt {24} }}{7}\).. .

معلم: آفرین، این راه کاملاً درست است، ولی کدام مقدار قابل قبول است؟

محمد مهدی: چون θ زاویه ای در ربع …دوم… است، پس طول نقطهٔ P منفی است و از این رو x=…\( - \frac{{\sqrt {24} }}{7}\).. قابل قبول است.

معلم: استدلال محمدمهدی کاملاً منطقی است و P نقطه ای به مختصات \(( - \frac{{\sqrt {24} }}{7}\;,\;\frac{5}{7})\) است. در نتیجه:

\(\begin{array}{l}\cot \theta = \frac{x}{y} = \frac{{ - \sqrt {24} }}{5}{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \\\\\tan \theta = \frac{y}{x} = \frac{5}{{\sqrt {24} }}{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \\\\\cos \theta = x = - \frac{{\sqrt {24} }}{7}\end{array}\)