1736019749.png)
جواب تمرین صفحه 33 درس 2 حسابان دوازدهم (مثلثات)
تعداد بازدید : 78.77Mپاسخ تمرین صفحه 33 حسابان دوازدهم
-گام به گام تمرین صفحه 33 درس مثلثات
-تمرین صفحه 33 درس 2
-شما در حال مشاهده جواب تمرین صفحه 33 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
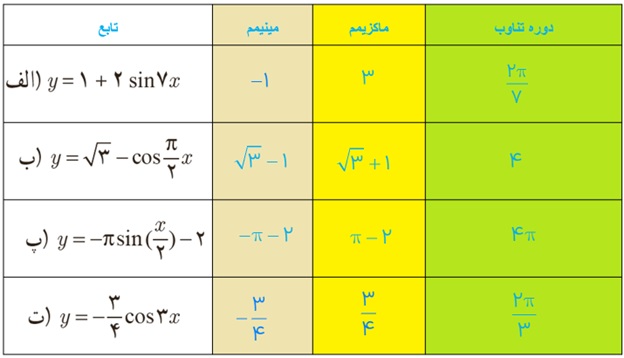
1 دوره تناوب و مقادیر ماکزیمم و مینیمم هر یک از توابع زیر را به دست آورید.
الف y = 1 + 2sin7x
ب \(y = \sqrt 3 - \cos \frac{\pi }{2}x\)
پ \(y = - \pi \sin (\frac{\pi }{2}) - 2\)
ت \(y = - \frac{3}{4}\cos 3x\)
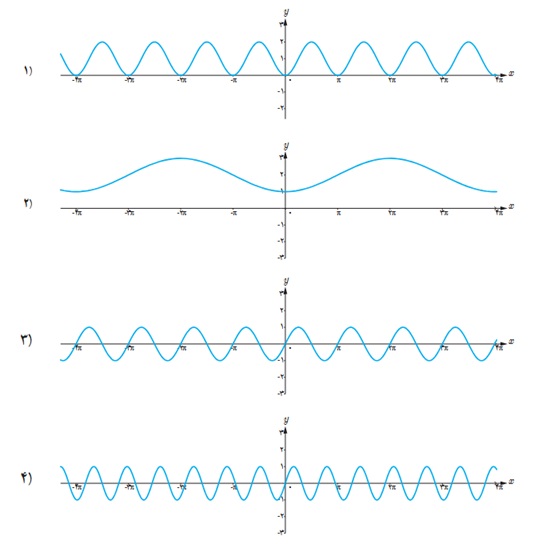
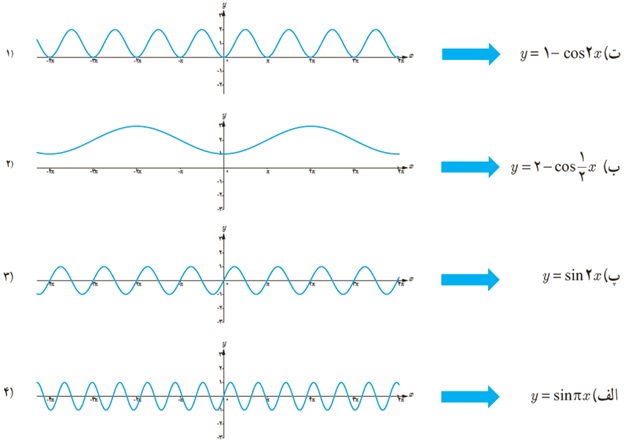
2 هر یک از توابع داده شده را با نمودارهای زیر نظیر کنید.
الف y = sinπx
ب \(y = 2 - \cos \frac{1}{2}x\)
پ y = sin2x
ت y = 1 - cos2x
3 در هر مورد ضابطهٔ تابعی مثلثاتی با دورهٔ تناوب و مقادیر ماکزیمم و مینیمم داده شده بنویسید.
الف \(T = \pi \;\;\;,\;\;\;\max = 3\;\;\;,\;\;\;\min = - 3\)
ب \(T = 3\;\;\;,\;\;\;\max = 9\;\;\;,\;\;\;\min = 3\)
پ \(T = 4\pi \;\;\;,\;\;\;\max = - 1\;\;\;,\;\;\;\min = - 7\)
ت \(T = \frac{\pi }{2}\;\;\;,\;\;\;\max = 1\;\;\;,\;\;\;\min = - 1\)
الف \(T = \pi \;\;\;,\;\;\;\max = 3\;\;\;,\;\;\;\min = - 3 \to y = 3\sin 2x\)
ب \(T = 3\;\;\;,\;\;\;\max = 9\;\;\;,\;\;\;\min = 3 \to y = 3\sin \frac{{2\pi }}{3}x + 6\)
پ \(T = 4\pi \;\;\;,\;\;\;\max = - 1\;\;\;,\;\;\;\min = - 7 \to y = 3\sin \frac{1}{2}x - 4\)
ت \(T = \frac{\pi }{2}\;\;\;,\;\;\;\max = 1\;\;\;,\;\;\;\min = - 1 \to y = \cos 4x\)
4 ضابطهٔ مربوط به هر یک از نمودارهای داده شده را بنویسید.
الف
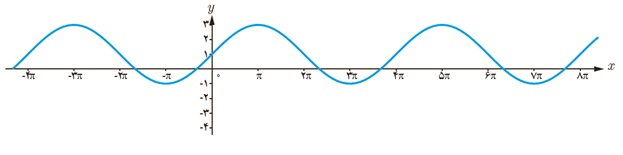
ب
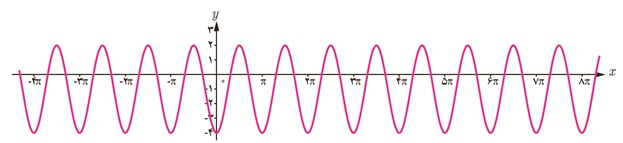
الف \(y = 2\sin \frac{1}{2}x + 1\)
ب \(y = - 3\cos 2x\; - 1\)
5 کدام یک از جملات زیر درست و کدام یک نادرست است؟
الف تابع تانژانت در دامنه اش صعودی است.
ب می توان بازه ای یافت که تابع تانژانت در آن نزولی باشد.
پ تابع تانژانت در هر بازه که در آن تعریف شده باشد، صعودی است.
الف نادرست
ب نادرست
پ درست
6 با توجه به محورهای سینوس و تانژانت، در موارد زیر مقادیر sinα و tanα را با هم مقایسه کنید:
الف \(0 < \alpha < \frac{\pi }{2}\)
ب \(\frac{{3\pi }}{2} < \alpha < 2\pi \)
الف \(\begin{array}{l}\sin \alpha > 0\quad ,\quad \sin \nearrow \\\tan \alpha > 0\quad ,\quad \tan \nearrow \end{array}\)
ب \(\begin{array}{l}\sin \alpha < 0\quad ,\quad \sin \nearrow \\\tan \alpha < 0\quad ,\quad \tan \nearrow \end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
